Hash Tables
The hash table is the most commonly used data structure for implementing associative arrays. It features \(O(1)\) average search times, making it an efficient data structure to use for caching, indexing, and other time-critical operations.
Minimal Implementation
Hash tables are implemented by using an array of fixed size. To insert a key/value pair, the key is first hashed. Since hashes are just large integers, the hash is then taken modulo the size of the array, yielding an index. The key/value pair is then inserted into a bucket at that index.
Buckets are required because the birthday problem says that hash collisions are inevitable; so instead of each index storing a single key/value pair, it stores a bucket of pairs. In the most basic implementation, buckets are implemented by using linked lists.
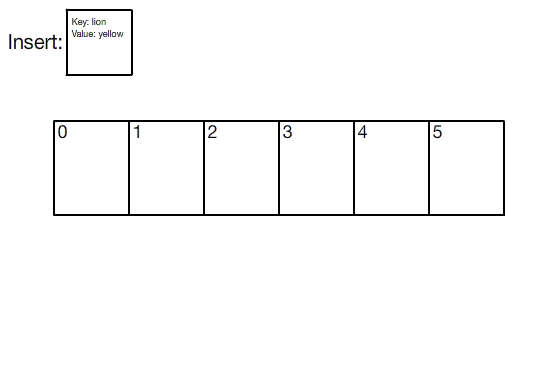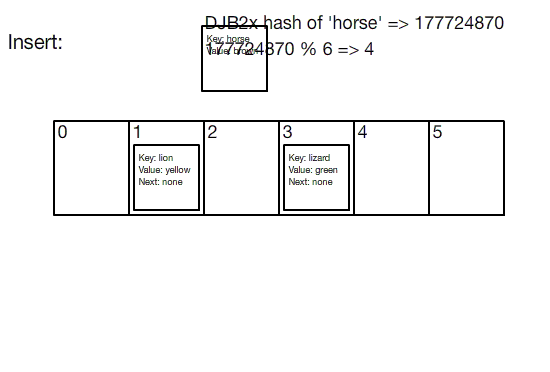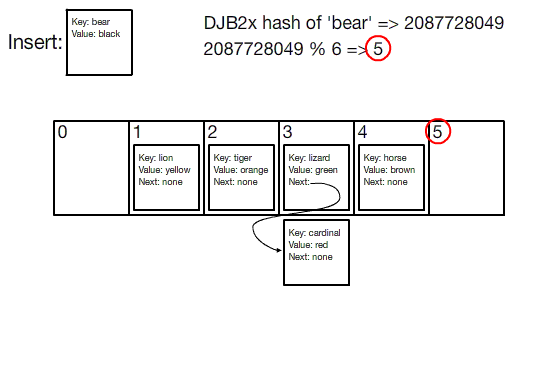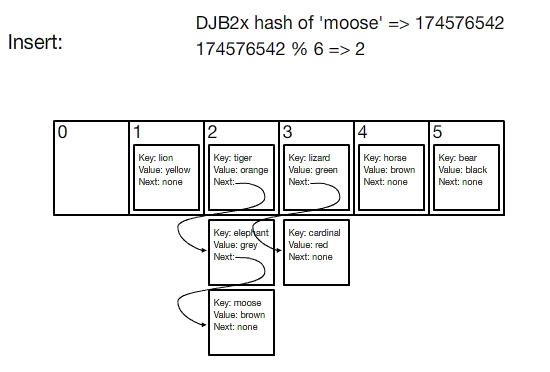 Visualization of hash table insertion
Visualization of hash table insertion
Notice that the size of the bucket array doesn't limit the number of key/value pairs that can be stored in the hash table. In the above animation, the bucket array is of length 6, but 8 key/value pairs are inserted. This ratio of the number of pairs to the number of buckets is called the load factor.
\[\text{Load Factor} = \frac{\text{number of pairs}}{\text{number of buckets}}.\]
As the load factor increases, collisions are more likely to occur. As more and more collisions occur, performance degrades. In the absolute worst case, a hash table with only 1 bucket, the hash table behaves like a linked list with \(O(n)\) search, insertion, and deletion times.
 Bucket length as a function of load factor
Bucket length as a function of load factor
Asymptotic Complexity
See also: big O notation.
| Average | Worst | |
| Space | \(O(n)\) | \(O(n)\) |
| Search | \(O(1)\) | \(O(n)\) |
| Insert | \(O(1)\) | \(O(n)\) |
| Delete | \(O(1)\) | \(O(n)\) |
Sample Python implementation
This sample is a minimum implementation of a hash table whose keys must be strings. It uses DJB2 (xor variant) as its hashing function. Buckets are implemented with linked lists. (Note that Python's built-in Dictionary type is implemented with a hash table. This sample implementation is purely for academic purposes.)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 | |
Try it out:
1 2 3 4 5 6 7 8 9 10 | |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | |