Max-flow Min-cut Algorithm
The max-flow min-cut theorem is a network flow theorem. This theorem states that the maximum flow through any network from a given source to a given sink is exactly the sum of the edge weights that, if removed, would totally disconnect the source from the sink. In other words, for any network graph and a selected source and sink node, the max-flow from source to sink = the min-cut necessary to separate source from sink. Flow can apply to anything. For instance, it could mean the amount of water that can pass through network pipes. Or, it could mean the amount of data that can pass through a computer network like the Internet.
Max-flow min-cut has a variety of applications. In computer science, networks rely heavily on this algorithm. Network reliability, availability, and connectivity use max-flow min-cut. In mathematics, matching in graphs (such as bipartite matching) uses this same algorithm. In less technical areas, this algorithm can be used in scheduling. For example, airlines use this to decide when to allow planes to leave airports to maximize the "flow" of flights.

What is the fewest number of green tubes that need to be cut so that no water will be able to flow from the hydrant to the bucket?
Assume that the gray pipes in this system have a much greater capacity than the green tubes, such that it's the capacity of the green network that limits how much water makes it through the system per second. Additionally, assume that all of the green tubes have the same capacity as each other.
The network can be severed in 5 cuts:

How to know where to cut and a proof that five cuts are required:
If this system were real, a fast way to solve this puzzle would be to allow water to blast from the hydrant into the green hose system. Once water is flowing through the network at the highest capacity the system can manage, look at how the water is flowing through the system and follow these two steps repeatedly until the network is fully severed:
1) Find a tube-segment that water is flowing through at full capacity. Somewhere along the path that each stream of water takes, there will be at least one such tube (otherwise, the system isn't really being used at full capacity).
2) Once you've found such a tube-segment, test squeezing it shut. If squeezing it shut reduces the capacity of the system because the water can't find another way to get through, then cut it. Again, somewhere along the path each stream of water takes, there will be at least one such tube-segment, otherwise, the system isn't really being used at full capacity.
With each cut, the capacity of the system will decrease until, at last, it decreases to 0.
An illustration of how knowing the "Max-Flow" of a network allows us to prove that the"Min-Cut" of the network is, in fact, minimal:
In the center image above, you can see one example of how the hose system might be used at full capacity. Each of the black lines represents a stream of water totally filling the tubes it passes through. In this image, as many distinct paths as possible have been drawn in across the system. The distinct paths can share vertices but they cannot share edges. The maximum number of paths that can be drawn given these restrictions is the "max-flow" of this network. In this example, the max flow of the network is five (five times the capacity of a single green tube).
The final picture illustrates how cutting through each of these paths once along a single 'cutting path' will sever the network. Five cuts are required, otherwise there would be at least one unaffected stream of water. In other words, being able to find five distinct paths for water to stream through the system is proof that at least five cuts are required to sever the system. Therefore, five is also the "min-cut" of the network. The water-pushing technique explained above will always allow you to identify a set of segments to cut that fully severs the network with the 'source' on one side and the 'sink' on the other.
Contents
Intuition
All networks, whether they carry data or water, operate pretty much the same way. The network wants to get some type of object (data or water) from the source to the sink. The amount of that object that can be passed through the network is limited by the smallest connection between disjoint sets of the network. Even if other edges in this network have bigger capacities, those capacities will not be used to their fullest.
In the example below, you can think about those networks as networks of water pipes. Each arrow can only allow 3 gallons of water to pass by. So, the network is limited by whatever partition has the lowest potential flow.
1. \(\ \) Look at the following graphic. It is a network with four edges. The source is on top of the network, and the sink is below the network. Each edge has a maximum flow (or weight) of 3. How much flow can pass through this network at any given time?
Network example 1
The answer is 3. The bottom three edges can pass 9 among the three of them, true. However, the limiting factor here is the top edge, which can only pass 3 at a time. This is the intuition behind max-flow min-cut. The minimum cut will be the limiting factor.
As you can see in the following graphic, by splitting the network into disjoint sets, we can see that one set is clearly the limiting factor, the top edge. The top set's maximum weight is only 3, while the bottom is 9. The top half limits the flow of this network.
The same network split into disjoint sets
2. \(\ \) What's the maximum flow for this network?
Network example 2
The answer is still 3! The limiting factor is now on the bottom of the network, but the weights are still the same, so the maximum flow is still 3. The same network, partitioned by a barrier, shows that the bottom edge is limiting the flow of the network.
The same network, partitioned
Let's look at another water network that has edges of different capacities.
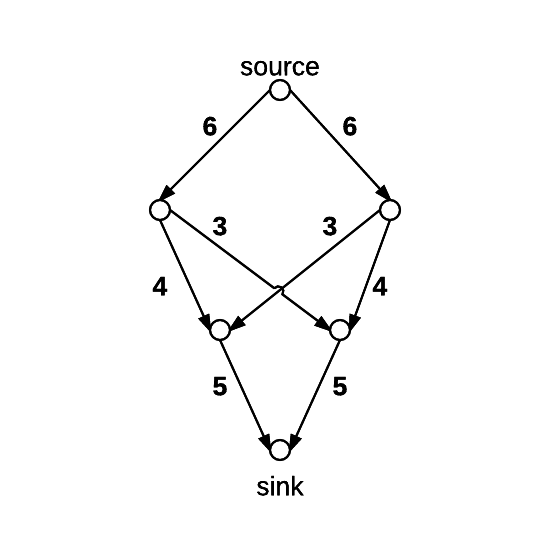 Water flow network
Water flow network
In this graphic, each edge represents the amount of water, in gallons, that can pass through it at any given time.
1. \(\ \) What is the max-flow of this network?
The answer is 10 gallons. Let's walk through the process starting at the source, taking things level by level:
1) 6 gallons of water can pass from the source to both vertices at the next level down. That makes a total of 12 gallons so far.
2) From here, only 4 gallons can pass down the outside edges. However, there is another edge coming out of each edge that has a capacity of 3. 4 gallons plus 3 gallons is more than the 6 gallons that arrived at each node, so we can pass all of the water through this level.
3) From this level, our only path to the sink is through an edge with capacity 5. That means we can only pass 5 gallons of water per vertex, coming out to 10 gallons total. That is the max-flow of this network.
It's important to understand that not every edge will be carrying water at full capacity. This is one example of how the network might look from a capacity perspective. Now, every edge displays how much water it is currently carrying over its total capacity.
Water flow network capacity
Technical Overview
There are a few key definitions for this algorithm. First, the network itself is a directed, weighted graph. That is, it is composed of a set of vertices connected by edges. These edges only flow in one direction (because the graph is directed) and each edge also has a maximum flow that it can handle (because the graph is weighted).
There are two special vertices in this graph, though. The source is where all of the flow is coming from. All edges that touch the source must be leaving the source. And, there is the sink, the vertex where all of the flow is going. Similarly, all edges touching the sink must be going into the sink.
A cut is a partitioning of the network, \(G\), into two disjoint sets of vertices. These sets are called \(S\) and \(T\). \(S\) is the set that includes the source, and \(T\) is the set that includes the sink. The only rule is that the source and the sink cannot be in the same set. A cut has two important properties. The first is the cut-set, which is the set of edges that start in \(S\) and end in \(T\). The second is the capacity, which is the sum of the weights of the edges in the cut-set. Look at the following graphic for a visual depiction of these properties.
 Cut S with capacity 7
Cut S with capacity 7
In this picture, the two vertices that are circled are in the set \(S\), and the rest are in \(T\). \(S\) has three edges in its cut-set, and their combined weights are 7, the capacity of this cut. The goal of max-flow min-cut, though, is to find the cut with the minimum capacity.
Algorithm
There are many specific algorithms that implement this theorem in practice. The most famous algorithm is the Ford-Fulkerson algorithm, named after the two scientists that discovered the max-flow min-cut theorem in 1956.
Proof
First, there are some important initial logical steps to proving that the maximum flow of any network is equal to the minimum cut of the network.
Lemma 1:
For any flow \(f\) and any cut \((S, T)\) on a network, it holds that \(f \leq \text{capacity}(S, T)\). This makes sense because it is impossible for there to be more flow than there is room for that flow (or, for there to be more water than the pipes can fit).
Corollary 2:
Due to Lemma 1, we have a clear next step. For the maximum flow \(f^{*}\) and the minimum cut \((S, T)^{*}\), we have \(f^{*} \leq \text{capacity}\big((S, T)^{*}\big).\)
These two mathematical statements place an upper bound on our maximum flow.
Proof:
Begin with any flow \(f\). This is possible because the zero flow is possible (where there is no flow through the network). Then the following process of residual graph creation is repeated until no augmenting paths remain.
Define augmenting path \(p_a\) as a path from the source to the sink of the network in which more flow could be added (thus augmenting the total flow of the network).
We want to create, at each step of this process, a residual graph \(G_f\). To do so, first find an augmenting path \(p_a\) with a given minimum capacity \(c_p\). That is, \(c_p\) is the lowest capacity of all the edges along path \(p_a\).
For each edge with endpoints \((u, v)\) in \(p_a\), increase the flow from \(u\) to \(v\) by \(c_p\) and decrease the flow from \(v\) to \(u\) by \(c_p\). This might require the creation of a new edge in the backward direction. This process does not change the capacity constraint of an edge and it preserves non-negativity of flows. Also, this increases the flow from the source to the sink by exactly \(c_p\). This is how a residual graph is created.
Now, it is important to note that our new flow \(f^{*} = f + c_p\) no longer contains the augmenting path \(c_p\). This is because the process of augmenting our flow by \(c_p\) has either given one of the forward edges a maximum capacity or one of the backward edges a flow of zero.
This process is repeated until no augmenting paths remain. Once that happens, denote all vertices reachable from the source as \(V\) and all of the vertices not reachable from the source as \(V^c\). Trivially, the source is in \(V\) and the sink is in \(V^c\). Importantly, the sink is not in \(V\) because there are no augmenting paths and therefore no paths from the source to the sink.
Consider a pair of vertices, \(u\) and \(v\), where \(u\) is in \(V\) and \(v\) is in \(V^c\). The flow of \((u, v)\) must be maximized, otherwise we would have an augmenting path. And, the flow of \((v, u)\) must be zero for the same reason. Therefore, \[\text{flow}(u, v) = \text{capacity}(u, v)\] for all edges with \(u\) in \(V\) and \(v\) in \(V^c\), so \[\text{flow}(V, V^{c}) = \text{capacity}(V, V^{c}).\] Then, by Corollary 2, \[f^{*} = \text{capacity}(S, T)^{*}.\]
Extensions
Networks can look very different from the basic ones shown in this wiki. However, the max-flow min-cut theorem can still handle them. What about networks with multiple sources like the one below (each source vertex is labeled S)?
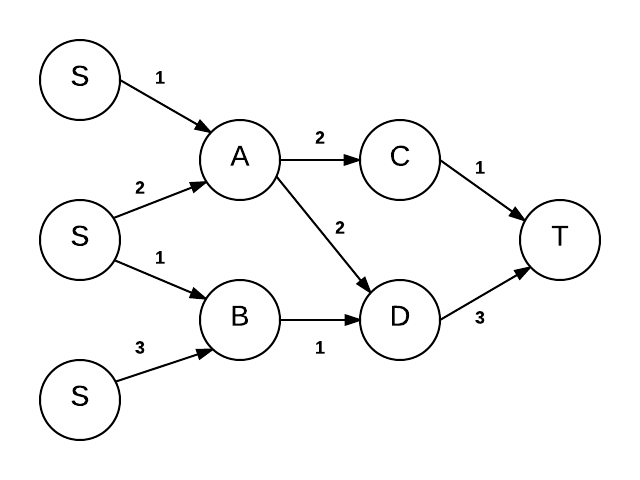 Flow network with multiple sources
Flow network with multiple sources
With no trouble at all, a new network can be created with just one source. This source connects to all of the sources from the original version, and the capacity of each edge coming from the new source is infinity. The same process can be done to deal with multiple sink vertices.
 Flow network with consolidated source vertex
Flow network with consolidated source vertex
This small change does nothing to affect the flow potential for the network because these only added edges having an infinite capacity and they cannot contribute to any bottleneck. This allows us to still run the max-flow min-cut theorem.
