
In number theory, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that if two numbers \(a\) and \(n\) are relatively prime (if they share no common factors apart from 1) then:
\[a^{\phi(n)} \equiv 1 \pmod n,\] where \(\phi(n)\) is Euler's totient function, which counts the number of positive integers \(\le n\) which are relatively prime to \(n.\)
Expect to see and learn how to solve questions like this one:
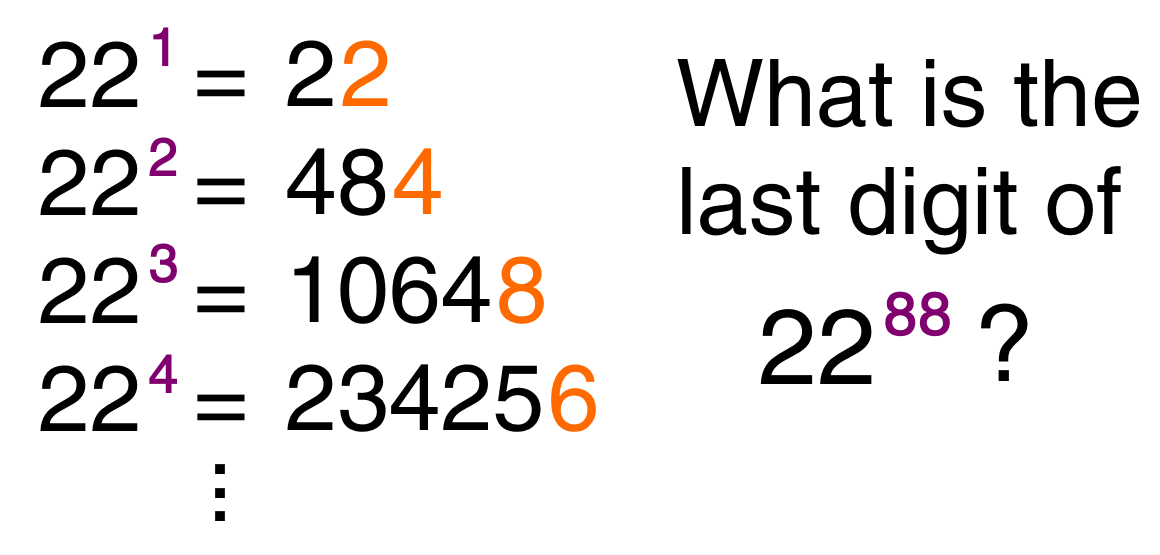
Euler’s Theorem is a generalization of Fermat's little theorem. It arises in many applications of elementary number theory, including calculating the last digits of large powers and, relatedly, it is part of the theoretical foundation for the RSA cryptosystem (online security).