Naive Bayes Classifier
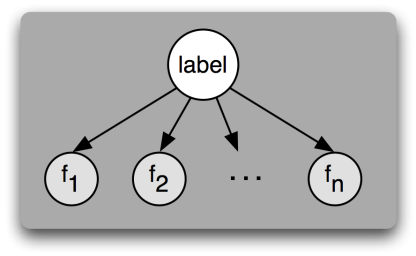 An influence diagram of \(n\) features \(f_1, \dots, f_n\)conditionally independent on a class label, i.e. features are considered independent from one another. Because there are no arrows between features, the value of one feature cannot affect the value of another feature. The only thing that can affect a feature's values is the label, indicated by the arrow pointing from the label to each feature.[1]
An influence diagram of \(n\) features \(f_1, \dots, f_n\)conditionally independent on a class label, i.e. features are considered independent from one another. Because there are no arrows between features, the value of one feature cannot affect the value of another feature. The only thing that can affect a feature's values is the label, indicated by the arrow pointing from the label to each feature.[1]
Naive Bayes, also known as Naive Bayes Classifiers are classifiers with the assumption that features are statistically independent of one another. Unlike many other classifiers which assume that, for a given class, there will be some correlation between features, naive Bayes explicitly models the features as conditionally independent given the class. While this may seem an overly simplistic (naive) restriction on the data, in practice naive Bayes is competitive with more sophisticated techniques and enjoys some theoretical support for its efficacy[2].
Because of the independence assumption, naive Bayes classifiers are highly scalable and can quickly learn to use high dimensional features with limited training data. This is useful for many real world datasets where the amount of data is small in comparison with the number of features for each individual piece of data, such as speech, text, and image data. Examples of modern applications include spam filtering[3], automatic medical diagnoses, medical image processing[4], and vocal emotion recognition[5].
Overview
Performing classification on input vectors \(\vec{x}=\{x_1, ..., x_n\}\) of \(n\) features involves assigning each vector \(\vec{x}\) to a class \(C_k\). For example, if one is seeking to classify trees using the features \(loses\ its\ leaves\ in\ the\ winter\) and \(height\), the possible classes may be \(C_1=\text{oak tree}\), \(C_2=\text{douglas fir}\), and \(C_3=\text{giant sequoia}\).
Modeling this classification function typically involves creating a probability distribution modeling the joint distribution \(p(\vec{x}, C_k)\) and then using Bayes' Theorem plus the class prior probabilities \(p(C_k)\) to calculate the class probability \(p(C_k|\vec{x})\) conditioned on \(\vec{x}\). In the example above, the joint function would be a function that models that chances of both the class label, which specifies the species of tree, and specific values for the tree features co-occurring.
For example, the chances of \(p(C_2=\text{douglas fir}, loses\ its\ leaves\ in\ the\ winter=\text{True}, height=\text{20 ft})\) would be unlikely since most Douglas firs don't lose their leaves in the winter. Once this distribution is found, one can use Bayes' Theorem to calculate the possibility of the tree species given the tree features. For example, the highest class probability for \(p(C_k \mid loses\ its\ leaves\ in\ the\ winter=\text{True}, height=\text{20 ft})\) would be \(k=1\), since oak trees are the only one of the three species that loses its leaves in the winter.
Curse of Dimensionality
Unfortunately, for large feature spaces learning \(p(\vec{x}, C_k)=p(x_1, ...x_n, C_k)\) takes an exponentially large amount of training data in the dimension \(n\), the number of features. This is known as the curse of dimensionality, which intuitively says that as the number of features grows, the number of "bins" in the space spanned by those features grows exponentially fast. Accurately learning a distribution requires an amount of data proportional to the number of bins (i.e. empty bins can't be learned), so learning classifiers on high dimensional data with small datasets presents a problem.
The Naive Assumption
A simplifying assumption is that the features are conditionally independent given the class \(C_k\). As demonstrated below, this avoids the curse-of-dimensionality by allowing the join distribution \(p(x_1, ...x_n, C_k)\) to be decomposed into \(n + 1\) factors (\(n\) features plus the class prior \(p(C_k)\)), thereby reducing the number of bins from \(O(\exp(n))\) to \(O(n)\). In the tree example, this would be akin to making the assumption that given the correct species label \(C_k\), whether a tree sheds its leaves in the winter doesn't affect how tall the tree is. This is probably true for most trees, since a species of tree's height is generally not affected by its shedding, but only by the species itself.
The assumption that the features are independent is considered "naive" since this is, unlike the previous tree example, generally false. For example, in the classification of coins, given a sample coin's weight \(w\) and diameter \(d\), naive Bayes would assume that the weight and diameter are independent conditioned on the type of the coin. However, since the weight of a coin is roughly \(w= g V \rho = g (\pi (\frac{d}{2})^2 h) \rho = O(d^2)\) (where \(g\) is the gravitational constant, \(V\) is the volume, and \(\rho\) is the density) is an increasing function of \(d\), the weight is very positively correlated with the diameter for every type of coin. However, even with this typically false assumption, it turns out that for a large number of features, e.g. \(n=100\), naive Bayes yields good performance in practice.
Model
Given a data point \(\vec{x}=\{x_1, ..., x_n\}\) of \(n\) features, naive Bayes predicts the class \(C_k\) for \(\vec{x}\) according to the probabiltiy
\[p(C_k|\vec{x}) = p(C_k|x_1, ..., x_n) \text{ for } k=1, ..., K\]
Using Bayes' Theorem, this can be factored as
\[p(C_k|\vec{x})=\frac{p(\vec{x}|C_k)p(C_k)}{p(\vec{x})}=\frac{p(x_1, ..., x_n|C_k)p(C_k)}{p(x_1, ..., x_n)}\]
Using the chain rule, the factor \(p(x_1, ..., x_n|C_k)\)in the numerator can be further decomposed as
\[p(x_1, ..., x_n|C_k)=p(x_1|x_2, ... x_n, C_k)p(x_2|x_3, ..., x_n, C_k)...p(x_{n-1}|x_n, C_k)p(x_n|C_k)\]
At this point, the "naive" conditional independence assumption is put into play. Specifically, naive Bayes models assume that feature \(x_i\) is independent of feature \(x_j\) for \(i \ne j\) given the class \(C_k\). Using the previous decomposition, this can be formulated as
\[p(x_i|x_{i+1}, ..., x_n|C_k)=p(x_i|C_k) \implies p(x_1, ..., x_n|C_k)=\prod_{i=1}^np(x_i|C_k)\]
Thus, \[\begin{align} p(C_k|x_1, ..., x_n) & \varpropto p(C_k, x_1, ..., x_n) \\ & \varpropto p(C_k)p(x_1, ..., x_n|C_k) \\ & \varpropto p(C_k) \ p(x_1|C_k) \ p(x_2|C_k)...p(x_n|C_k) \\ & \varpropto p(C_k) \prod_{i=1}^n p(x_i|C_k)\,. \end{align}\]
Practically speaking, the class conditional feature probabilities \(p(x_i|C_k)\) are usually modeled using the same class of probability distribution, such as the binomial distribution or Gaussian distribution. In the latter case, the class conditional distribution is known as a product of gaussians and has some convenient computational properties that simplify the optimization equations for parameter learning.
Classification
Naive Bayes gives the probability of a data point \(\vec{x}\) belonging to class \(C_k\) as proportional to a simple product of \(n+1\) factors (the class prior \(p(C_k)\) plus \(n\) conditional feature probabilities \(p(x_i|C_k)\)). Since classification involves assigning the class \(C_k\) to the data point for which the value \(p(C_k|\vec{x}\) is greatest, this proportional product can be used to determine the most likely class assignment. Specifically,
\[p(C_a) \prod_{i=1}^n p(x_i|C_a) \gt p(C_b) \prod_{i=1}^n p(x_i|C_b) \implies p(C_a|x_1, ..., x_n) \gt p(C_b|x_1, ..., x_n)\]
Thus, the most likely class assignment for a data point \(\vec{x}=x_1, ..., x_n\) can be found by calculating \(p(C_k) \prod_{i=1}^n p(x_i|C_k)\) for \(k=1, ..., K\) and assigning \(\vec{x}\) the class \(C_k\) for which this value is largest. In mathematical notation, this is defined
\[\hat{C} = \underset{k \in \{1, ..., K\}}{\operatorname{argmax}} \ p(C_k) \prod_{i=1}^n p(x_i | C_k)\]
where \(\hat{C}\) is the estimated class for \(\vec{x}\) given its features \(x_1, ..., x_n\).
Model the following dataset for males and females using a Gaussian naive Bayes classifier. Then, for a sample with \(height=6 \text{ ft}\), \(weight=130 \text{ lbs}\), and \(shoe=8 \text{ inches}\), predict whether that sample is male or female given the trained model.
Height (ft) Weight (lbs) Shoe Size (in) Gender 6.00 180 12 male 5.92 190 11 male 5.58 170 12 male 5.92 165 10 male 5.00 100 6 female 5.50 150 8 female 5.42 130 7 female 5.75 150 9 female
Since the classifier is a Gaussian naive Bayes model, the feature distributions conditioned on the classes (\(male\) or \(female\)) will be Gaussian distributions. Thus,
\[\begin{align} p(height \; | \; male) &= \mathcal{N}(height \; | \; \mu_{hm}, \sigma_{hm}) \\ p(weight \; | \; male) &= \mathcal{N}(weight \; | \; \mu_{wm}, \sigma_{wm}) \\ p(shoe \; | \; male) &= \mathcal{N}(shoe \; | \; \mu_{sm}, \sigma_{sm}) \\ \\ p(height \; | \; female) &= \mathcal{N}(height \; | \; \mu_{hf}, \sigma_{hf}) \\ p(weight \; | \; female) &= \mathcal{N}(weight \; | \; \mu_{wf}, \sigma_{wf}) \\ p(shoe \; | \; female) &= \mathcal{N}(shoe \; | \; \mu_{sf}, \sigma_{sf}) \end{align}\]
where \(\mathcal{N}(\dot \ | \; \mu, \sigma)\) is the Gaussian probability density function with mean \(\mu\) and standard deviation \(\sigma\).
Using maximum likelihood estimates of the mean and the unbiased variance gives
\[p(male) = p(female) = \frac{1}{2}\]
height mean height variance weight mean weight variance shoe size mean shoe size variance \(male\) \(\mu_{hm}=5.855\) \(\sigma_{hm}^2=.0350\) \(\mu_{wm}=176.25\) \(\sigma_{wm}^2=122.9\) \(\mu_{sm}=11.25\) \(\sigma_{sm}^2=.9167\) \(female\) \(\mu_{hf}=5.418\) \(\sigma_{hf}^2=.0972\) \(\mu_{wf}=132.5\) \(\sigma_{wf}^2=558.3\) \(\mu_{sf}=7.5\) \(\sigma_{sf}^2=1.667\) Plugging these into the proportional class probabilities conditioned on the \(height\), \(weight\), and \(shoe\) data gives
\[\begin{align} p(male \; | \; height, weight, shoe) &\propto p(male) \ p(height \; | \; male) \ p(weight \; | \; male) \ p(shoe \; | \; male) \\ &\propto p(male) \ \mathcal{N}(height \;|\; \mu_{hm}, \sigma_{hm}) \ \mathcal{N}(weight \;|\; \mu_{wm}, \sigma_{wm}) \ \mathcal{N}(shoe \;|\; \mu_{sm}, \sigma_{sm}) \\ &\propto \frac{1}{2} \ \mathcal{N}(6 \;|\; 5.855, \sqrt{.0350}) \ \mathcal{N}(130 \;|\; 176.25, \sqrt{122.9}) \ \mathcal{N}(8 \;|\; 11.25, \sqrt{.9167}) \\ &=.5 \times 1.579 \times 5.988 \cdot 10^{-6} \times 1.311 \cdot 10^{-3} \\ &=6.120 \cdot 10^{-9} \end{align}\]
\[\begin{align} p(female \; | \; height, weight, shoe) &\propto p(female) \ p(height \; | \; female) \ p(weight \; | \; female) \ p(shoe \; | \; female) \\ &\propto p(female) \ \mathcal{N}(height \;|\; \mu_{hf}, \sigma_{hf}) \ \mathcal{N}(weight \;|\; \mu_{wf}, \sigma_{wf}) \ \mathcal{N}(shoe \;|\; \mu_{sf}, \sigma_{sf}) \\ &\propto \frac{1}{2} \ \mathcal{N}(6 \;|\; 5.418, \sqrt{.0972}) \ \mathcal{N}(130 \;|\; 132.5, \sqrt{558.3}) \ \mathcal{N}(8 \;|\; 7.5, \sqrt{1.667}) \\ &=.5 \times 2.235 \cdot 10^{-1} \times 1.679 \cdot 10^{-2} \times 2.867 \cdot 10^{-1} \\ &=5.378 \cdot 10^{-4} \end{align}\]
Thus, because \(6.120 \cdot 10^{-9} \lt 5.378 \cdot 10^{-4}\), the classifier predicts that the sample data came from a female.
Scalability and Efficiency
Since determining the most likely class for a data point \(\vec{x}=x_1, ..., x_n\) consists of calculating the product of \(n + 1\) factors \(K\) times, the big O notation for the runtime complexity of classification is \(O(nK)\). This is very computationally efficient (see embarrassingly parallel) and gives naive Bayes its high scalability since the runtime scales linearly in the number of features \(n\) and number of classes \(K\). This is especially useful in the domain of very high dimensional data, such as bag-of-words classifiers for large vocabulary corpora or high resolution image data, such as MRIs.
Naive Bayes learns conditional probability features for each feature separately, so it is very efficient for learning to classify small datasets, especially in the case that \(n \gt N\), where \(N\) is the number of training samples in \(X=\vec{x}_1, ...., \vec{x}_N\). This is often the case in medical imaging datasets, where a single MRI scan can have millions of features (pixels), but MRI scans are costly to obtain for a particular classification task, and thus, few and far between. As long as \(N\) is sufficiently large to accurately estimate the individual factors (\(N \approx 30K\) when \(p(x_i|C_k)\) is modeled by a Gaussian distribution), the number of features \(n\) can be any size.
References
- Bird, S. A Bayesian Network Graph. Retrieved July 1, 2015, from http://www.nltk.org/book/ch06.html
- Zhang, H. (2004). The Optimality of Naive Bayes. American Association for Artificial Intelligence, 1-6.
- Samahi, M. (1998). A Bayesian approach to filtering junk e-mail. AAAI'98 Workshop on Learning for Text Categorization, 1-8.
- Al-Aidaroos, K. (2012). Medical Data Classification with Naive Bayes Approach. Information Technology Journal, 11, 1166-1174.
- Choudhary, V. (2013). Vocal Emotion Recognition Using Naive Bayes Classifier. Procession of International Conference on Advances in Computer Science, AETACS, 378-382.