Bipolar Junction Transistors

Transistors are semiconductor devices that can be thought of as switches or signal amplifiers. Modern digital electronic devices, including logic gates among other things, are heavily dependent upon transistors.

A bipolar junction transistor relies on three $p$-type semiconductors and $n$-type semiconductors in contact.

Junction Transistors can be thought to be a pair of diodes. It consists of three semiconductor layers sandwiched together and hence is a three terminal device.

The three parts are as follows:

• Emitter: The left hand block of the transistor. It is moderately sized and heavily doped.
• Base: The central block. Thin and lightly doped.
• Collector: The right hand block. Large and moderately doped.

We use the letters $E,B,C$ to denote the Emitter, Base and Collector, respectively, in the transistor symbols.

transistor

As expected, this transistor is a sandwich of a $p$-type semiconductor between two $n$-type semiconductors.

circuit of NPN resistor

its symbol

Here is how the NPN transistor works:

• The emitter-base circuit is forward biased. Hence, the depletion layer in the emitter-base junction is reduced.
• The collector-base circuit is reverse biased. Hence, the depletion layer in the collector-base junction is increased.
• The electrons in the emitter are pushed towards the collector due to the electrostatic force provided by the negative terminal $V_{BE}$.
• Because the base is only lightly doped, only some of the electrons combine with holes in the base.
• The rest of the electrons move towards the collector and then out of it as $I_C$.

It is not too hard to see that (Why?)$$I_E = I_B + I_C.$$

The key point here is that the main charge carriers are the electrons.

Needless to say, PNP transistors are just the opposite.

Since the collector and the emitter are both $p$-type semiconductors, the principle charge carriers here are the holes. That explains why the current is in the reverse direction and that is a good way to explain the symbol as well.

The same relation of between $I_E, I_B, I_C$ holds.

These parameters are constant for constant voltages in the collector and emitter battery. These are the properties of the transistor by design.

We define the parameter $\alpha$ as $$\alpha = \frac{I_C}{I_E}$$ at a constant base-collector voltage

We define the parameter $\beta$ as $$\beta = \frac{I_C}{I_B}$$ at constant collector-emitter voltage

Usual $\alpha$ values range between 0.95 to 0.99 while that of $\beta$ ranges between 20 to 100.

Derive a relation between $\beta$ and $\alpha$.

---

We have

$$\begin{aligned} I_E &= I_B + I_C \\ \frac{1}{I_E} &= \frac{1}{I_B + I_C} \\ \frac{I_C}{I_E} &= \frac{I_C}{I_B + I_C} \\ \alpha &= \frac{I_C}{I_B + I_C} \\ \frac{1}{\alpha} &= \frac{I_B+I_C}{I_C} \\ \frac{1}{\alpha} &= \frac{1}{\beta} + 1 \\ \Rightarrow \frac{1}{\alpha} - \frac{1}{\beta} &= 1. \ _\square \end{aligned}$$

Recall that a key property of semiconductor is that they behave like insulators (the cut-off state) when the voltage is too low. This could help us use the transistor like a switch.

It seems really stupid to use a transistor as a switch in such a circuit. After all, we are still using a mechanical switch.
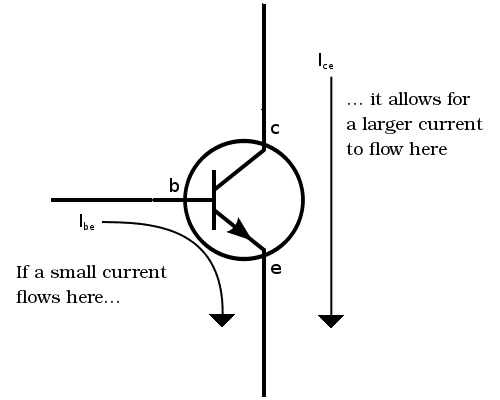
What is really important here is that the current that we need to provide in the base is really very small owing to the large value of $\beta$.
We could use this property to build, say, a light sensor.

Even though the solar cell can provide only feeble current, it is enough to switch on the circuit.

Amplification works on analog (infinitely divisible) signals. The key property of the signal that we need to preserve is its information content. To amplify is, roughly, to increase its amplitudes without destroying the information.

We all have seen loudspeakers which are basically amplifiers.

Amplification of an audio signal in audacity

The basic working principle of the amplification in bipolar junction transistors is that even though the current/signal is weak in the input circuit, it is what drives the output circuit, which has a strong signal. Only the disturbances or information gets ampified in the process.

This happens because of the difference of the large $R_{out}$ value to the small $R_{in}$ value.

We're interested in the voltage gain, i.e, the ratio of the change in voltage in the output to that of the input:

$$A_V = \frac{\Delta V_\text{out}}{\Delta V_\text{in}} = \frac{\Delta I_\text{out} R_\text{out}}{\Delta I_\text{in} R_\text{in}}.$$

However, $\frac{\Delta I_\text{out}}{\Delta I_\text{in}}$ is simply a constant such as $\alpha$ or $\beta$. So, $$A_V \propto \frac{R_\text{out}}{R_\text{in}}.$$

A very intutive analogy of amplification is working with a see-saw.

Pushing up one end of the lever causes the other end to go down by the same angle, yet the arcs subtended is much greater. Or, you could think of the amplification of the force in the load arm.

Over here, we observe that

$$\begin{aligned} V_\text{out} &= 10V - I_C \, 5 \Omega \\ &= 10V + I_E \, \alpha \, 5 \Omega \qquad (\text{Note that } I_E \text{ and } I_C \text{ are in opposite directions}.)\\ &= 10V + \frac{V_{in}}{1 \Omega} \, 5 \Omega \, \alpha \\ &= 10 V + 5 \, V_{in} \, \alpha. \end{aligned}$$

Though $\alpha$ is usually about 0.95 to 1, we have actually boosted the signal 5 times!

Suppose that you fed in the signal $V_\text{in}(t) = \sin t+\cos^2(t+2)$ and assume $\alpha = 1$. Here is what the input (blue) and output (red) would look like:

Note that the use of transistor as a switch is a special case of an amplifier.

This section is incomplete. Please edit this and remove the tag.

The amplifier circuits could be configured in various ways:

Configuration	Circuit	Current Gain	Voltage Gain	Power Gain
Common Emitter		$\beta$	$\beta \left(\frac{R_\text{out}}{R_\text{in}} \right )$	$\beta^2\left( \frac{R_\text{out}}{R_\text{in}} \right )$
Common Base		$\alpha$	$\alpha \left(\frac{R_\text{out}}{R_\text{in}} \right )$	$\alpha^2 \left( \frac{R_\text{out}}{R_\text{in}}\right )$
Common Collector