Boolean Algebra

As the name suggests, Boolean algebra is algebra of 0 and 1, or FALSE and TRUE.

▪ AND \((x\wedge y)\) is 1 if both \(x\) and \(y\) are 1, otherwise 0. It is also known as conjunction. (In more intuitive terms, A AND B is true only if both A and B are true.)

▪ OR \((x\vee y)\) is 0 if both \(x\) and \(y\) are 0, otherwise 1. (This is an "inclusive or". In other words, A OR B is true if one or the other or both are true.)

▪ NOT \((\sim x)\) is 0 if \(x\) is 1, and 1 if \(x\) is 0. (This simply flips from true to false, so NOT true is false, and NOT false is true.

A truth table is a table which gives input and output of an operator for different values of \(x\) and \(y.\)

Truth table for AND: \(\begin{array} {| c | c | c | c |} \hline x & y & x\wedge y \\ \hline 0 & 0 & 0\\ \hline 0 & 1 & 0\\ \hline 1 & 0 & 0\\ \hline 1 & 1 & 1\\ \hline \end{array}\)

Truth table for OR: \(\begin{array} {| c | c | c | c |} \hline x & y & x\vee y \\ \hline 0 & 0 & 0\\ \hline 0 & 1 & 1\\ \hline 1 & 0 & 1\\ \hline 1 & 1 & 1\\ \hline \end{array}\)

Truth table for NOT: \(\begin{array} {| c | c | c | c |} \hline x & ~x \\ \hline 0 & 1\\ \hline 1 & 0\\ \hline \end{array}\)

Draw the truth table for \(\sim (x\vee y)\).

---

\(\sim (x\vee y)\) implies NOT \(x\vee y\).

So we will first draw the table for \(x\vee y,\) and then reverse the final outputs in the end.

\(\begin{array} {| c | c | c | c |} \hline x & y & x\vee y & \sim (x\vee y) \\ \hline 0 & 0 & 0& 1\\ \hline 0 & 1 & 1& 0\\ \hline 1 & 0 & 1& 0\\ \hline 1 & 1 & 1& 0\\ \hline \end{array}\)

• Associativity

  • \(x\vee (y\vee z)=(x\vee y)\vee z\)

  • \(x\wedge (y\wedge z)=(x\wedge y)\wedge z\)

• Commutativity

  • \(x\vee y=y\vee x\)

  • \(x\wedge y=y\wedge x\)

• Distributivity

  • \(x\vee (y\wedge z)= (x\vee y)\wedge (x\vee z)\)

  • \(x\wedge (y\vee z)=(x\wedge y)\vee (x\wedge z)\)

• Identity

  • \(x\vee 0=x\)

  • \(x\wedge 1=x\)

• Annihilator

  • \(x\vee 1=1\)

  • \(x\wedge 0=0\)

• Idempotence

  • \(x\vee x=x\)

  • \(x\wedge x=x\)

• Absorption

  • \(x\vee (x\wedge y)=x\)

  • \(x\wedge (x\vee y)=x\)

• Complementation

  • \(x\vee \sim x=1\)

  • \(x\wedge \sim x=0\)

• Double negation

  • \(\sim (\sim x)=x\)

• De Morgan's Laws

  • \(\sim x\vee \sim y=\sim (x\wedge y)\)

  • \(\sim x\wedge \sim y=\sim (x\vee y)\)

\( \begin{array} {| c | c | c | c | c |} \hline x & y & x\to y & x \oplus y & x \equiv y \\ \hline 0 & 0 & 1 & 0& 1\\ \hline 1 & 0 & 0 & 1& 0\\ \hline 0 & 1 & 1 & 1& 0\\ \hline 1 & 1 & 1& 0 & 1\\ \hline \end{array}\)

• Material implication \(x \to y\) is defined as \(\sim x\vee y\): that is, \(y\) when \(x\) is true and \(x\) when \(x\) is false.

• Exclusive Or (XOR) \(x\oplus y\) is defined as \((x\vee y)\wedge \sim (x\wedge y)\).

• Equivalence (Boolean equality) \(x\equiv y\) is defined as \(\sim (x\oplus y)\). It is true when \(x\) and \(y\) are equal and false when they are not.

While boolean algebra is used often in coding, it has its most direct application in logic circuits. In a circuit a 0 can be considered a circuit that is OFF and a 1 is a circuit that is ON. AND, OR, and NOT gates each have their own symbol.

The inputs are on the left side of the gate and the outputs are on the right side.

0 1

The gates above are "inverters" or "NOT gates", that switch high voltage (1) to low voltage (0) or vice versa. What is the output?

0 1

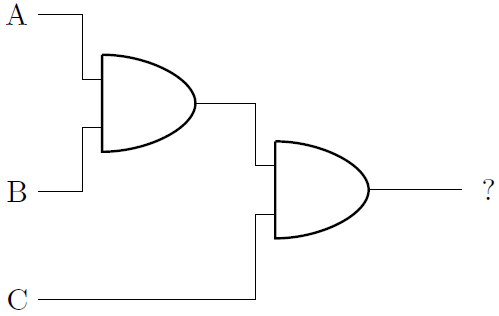
The AND gates in the diagram will output a 1 if both inputs are also 1.

If A = 1, B = 1, and C = 0, what will the final output be?

OR AND

The setup above works like a XOR gate (the output will be 1 if exactly one of the inputs is 1). However, the gate marked by a blue box is missing. What is the gate?