Dot Product - Direction Cosines
The direction cosines are three cosine values of the angles a vector makes with the coordinate axes.
Another way to think of this is to view them as the corresponding components of the unit vector pointing in the same direction.
Definition
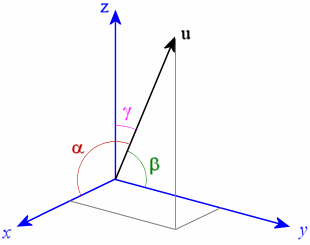
The three direction cosines are called \(l, m,\) and \( n, \) respectively.
For a vector \( \vec{v} = a \,\widehat{i} + b \,\widehat{j} + c \,\widehat{k} \) that subtends angles \(\alpha, \beta, \gamma\) with the \(x\)-, \(y\)-, \(z\)-axes, respectively, we have
\[\begin{align} l &= \cos \alpha = \frac{\vec{v} \cdot \widehat{i}}{\left\| \vec{v} \right\|} = \dfrac{a}{\left\| \vec{v} \right\|}\\\\ m &= \cos \beta = \frac{\vec{v} \cdot \widehat{j}}{\left\| \vec{v} \right\|} = \dfrac{b}{\left\| \vec{v} \right\|}\\\\ n &= \cos \gamma = \frac{\vec{v} \cdot \widehat{k}}{\left\| \vec{v} \right\|}= \dfrac{c}{\left\| \vec{v} \right\|}. \end{align}\]
Direction Cosines Theorem
\[l^2 + m^2 + n^2 = 1 \]
From the definition, it follows that
\[\begin{align} l &= \frac{a}{\sqrt{a^2 + b^2 + c^2}} \\\\ m &= \frac{b}{\sqrt{a^2 + b^2 + c^2}} \\\\ n &= \frac{c}{\sqrt{a^2 + b^2 + c^2}}. \end{align} \]
This is true because \(\left \| \vec{v} \right \| = \sqrt{a^2 + b^2 + c^2} \) by the Pythagorean theorem. Also, note that the dot product with a unit vector returns the component in the direction of that unit vector.
Squaring up and adding the three equations above, it is not too hard to see that
\[l^2 + m^2 + n^2 = 1. \ _\square\]
Calculating Angles between Vectors
In a similar way, we could use the dot product to calculate the angle between two vectors.
If \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\) are two vectors with an angle of \(\theta\) between them,
\[ \cos \theta = \frac{\vec{v_1} \cdot \vec{v_2}}{\left \| \vec{v_1} \right \| \left \| \vec{v_2} \right \| }.\]
This follows directly from the definition of dot product:
\[\begin{align} \vec{v_1} \cdot \vec{v_2} &= \left \| \vec{v_1} \right \| \left \| \vec{v_2} \right \| \cos \theta \\ \Rightarrow \cos \theta &= \frac{\vec{v_1} \cdot \vec{v_2}}{\left \| \vec{v_1} \right \| \left \| \vec{v_2} \right \| }. \ _\square \end{align}\]