Dot Product

The specific case of the inner product in Euclidean space, the dot product gives the product of the magnitude of two vectors and the cosine of the angle between them. Along with the cross product, the dot product is one of the fundamental operations on Euclidean vectors.

Let $\vec{a}$ and $\vec{b}$ be Euclidean vectors, and $\theta$ the angle between them. Then the dot product of $\vec{a}$ and $\vec{b}$ is denoted $a \cdot b$ and defined as

$$\vec{a} \cdot \vec{b} = \left\|\vec{a}\right\| \left\|\vec{b}\right\| \cos{\theta},$$

where $|\vec{a}|,$ for example, denotes the magnitude of $\vec{a}$.

Since the dot product is an operation on two vectors that returns a scalar value, the dot product is also known as the scalar product.

Geometrically, one can also interpret the dot product as

$$\vec{a} \cdot \vec{b} = \big( \left\|\vec{a}\right\| \big)\big( \left\|\vec{b}\right\| \cos{\theta} \big).$$

That is, one can view the dot product as the magnitude of $\vec{a}$ times the magnitude of the component of $\vec{b}$ that points along $\vec{a}$. $\big( \left\|\vec{b}\right\| \cos{\theta} \big)$ is the magnitude of the projection of $\vec{b}$ onto $\vec{a}:$

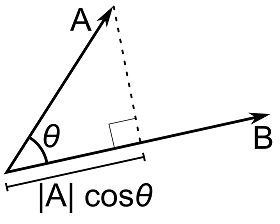
Similarly,

$$\vec{a} \cdot \vec{b} = \big( \left\|\vec{b}\right\| \big)\big( \left\|\vec{a}\right\| \cos{\theta} \big),$$

so the dot product can also be viewed the magnitude of $\vec{b}$ times the magnitude of the component of $\vec{a}$ that points along $\vec{b}$.

Since $\left\|\vec{a}\right\|$ and $\left\|\vec{b}\right\|$ are positive quantities, the sign of the dot product depends on $\theta:$

• If $\ \theta$ is acute, then $\cos{\theta}$ is positive, and therefore the dot product is positive.
• If $\ \theta$ is $90^{\circ}$, then the dot product is zero. Vectors whose dot product vanishes are said to be orthogonal.
• If $\ \theta$ is obtuse, then the dot product is negative.

Note that since the Euclidean basis unit vectors $\hat{x}$, $\hat{y}$, and $\hat{z}$ are mutually perpendicular, it holds that

$$\hat{x} \cdot \hat{y} = \hat{y} \cdot \hat{z} = \hat{x} \cdot \hat{z} = 0$$

and that

$$\hat{x} \cdot \hat{x} = \hat{y} \cdot \hat{y} = \hat{z} \cdot \hat{z} = 1.$$

Given that the magnitude of $\vec{a}$ is $7$ and that of $\vec{b}$ is $8$, find $\vec{a} \cdot \vec{b}$ when the angle between $\vec{a}$ and $\vec{b}$ is $$$$ $$\begin{array}{c}&\text{(i)}~ 60^\circ &&&\text{(ii)}~ 90^\circ &&&\text{(iii)}~ 120^\circ. \end{array}$$

---

To find the dot product, we use the formula $\vec{a} \cdot \vec{b} = \left\|\vec{a}\right\| \left\|\vec{b}\right\| \cos \theta$.

We know $\left\|\vec{a}\right\| = 7$ and $\left\|\vec{b}\right\| = 8,$ which implies $\vec{a} \cdot \vec{b} = 7 \times 8 \cos \theta = 56 \cos\theta.$ Hence the following answers:

(i) When $\theta = 60^\circ$, $\cos \theta = \frac{1}{2}$ and therefore $\vec{a} \cdot \vec{b} = 56 \times \frac{1}{2} = 28.$
(ii) When $\theta = 90^\circ$, $\cos \theta = 0$ and therefore $\vec{a} \cdot \vec{b} = 56 \times 0 = 0.$
(iii) When $\theta = 120^\circ$, $\cos \theta = - \frac{1}{2}$ and therefore $\vec{a} \cdot \vec{b} = 56 \times \left(- \frac{1}{2}\right) = - 28.$ $_\square$

If $\vec{c} = 4 \hat{\imath}$ and $\vec{d} = 2 \hat{\imath}$, what is $\vec{c} \cdot \vec{d}?$

---

We can apply the formula $\vec{c} \cdot \vec{d} = \left\|\vec{c}\right\| \left\|\vec{d}\right\| \cos \theta$.

We know $\left\|\vec{c}\right\| = 4$ and $\left\|\vec{d}\right\| = 2$. Also, the two vectors are parallel, so $\theta = 0$ and therefore $\cos \theta = 1.$
After we substitute the values in the formula, we get

$$\vec{c} \cdot \vec{d} = 4 \times 2 \times 1 = 8. \ _\square$$

The dot product has several important and useful properties. Their proofs are fairly straightforward and left as exercises for the reader.

$$\begin{array} { c | c } \text{Commutative} & \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u} \\ \hline \text{Distributive} & \vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w} \\ \hline \text{Scalar Multiplication} & (k_1 \vec{u}) \cdot (k_2 \vec{v}) = k_1 k_2 (\vec{u} \cdot \vec{v}) \\ \hline \text{Orthogonality} & \vec{u} \text{ and } \vec{v} \text{ are perpendicular if and only if } \vec{u} \cdot \vec{v} = 0 \\ \end{array}$$

Given $(5\vec{m}) \cdot (6 \vec{n}) = 34,$ find $(8 \vec{m}) \cdot (15 \vec{n})$.

---

The above property tells us that $(5\vec{m}) \cdot (6 \vec{n}) = 30 \vec{m} \cdot \vec{n}$. We are asked to find $(8 \vec{m}) \cdot (15 \vec{n})$, which is equivalent to $120 \vec{m} \cdot \vec{n}$.

Since $30 \vec{m} \cdot \vec{n} = 34$, it follows that $120 \vec{m} \cdot \vec{n} = 4 \times 30 \vec{m} \cdot \vec{n} = 4 \times 34 =136.\ _\square$

In Cartesian coordinates, the dot product takes on a convenient form. Suppose that $\vec{a}$ and $\vec{b}$ form angles $\alpha$ and $\beta$, respectively, with the $x$-axis. Recall that the representation in Cartesian coordinates becomes

$$\vec{a} = (x_a, y_a)$$

and

$$\vec{b} = (x_b, y_b),$$

where $x_a = |\vec{a}| \cos{\alpha}$, $y_a = |\vec{a}| \sin{\alpha}$, $x_b = |\vec{b}| \cos{\beta}$, and $y_b = |\vec{b}| \sin{\beta}$.

Therefore,

$$\begin{aligned} \vec{a} \cdot \vec{b} &= \left\|\vec{a}\right\|\left\|\vec{b}\right\| \cos(\beta - \alpha) \\ &= \left\|\vec{a}\right\|\left\|\vec{b}\right\| (\cos{\alpha} \cos{\beta} + \sin{\alpha}\sin{\beta}) \\ &= \left(\left\|\vec{a}\right\|\cos{\alpha}\right)\left(\left\|\vec{b}\right\|\cos{\beta}\right) + \left(\left\|\vec{a}\right\|\sin{\alpha}\right)\left(\left\|\vec{b}\right\|\sin{\beta}\right) \\ &= x_a x_b + y_a y_b. \end{aligned}$$

In other words, the product of two vectors in Cartesian coordinates is simply the sum of the product of each of the corresponding components of the two vectors. The same applies to vectors in more than two dimensions.

Dot Product in Cartesian Coordinates:

Suppose $\vec{a} = (a_1, a_2, \ldots, a_n)$ and $\vec{b} = (b_1, b_2, \ldots, a_n)$. Then

$$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n. \ _\square$$

Vectors $\vec{u}$, $\vec{v}$ and $\vec{u} - \vec{v}$ form a triangle, where $\theta$ is the angle between $\vec{u}$ and $\vec{v}$. Hence, we can apply cosine theorem to this triangle:

$$\begin{aligned}\left\|\vec{u} - \vec{v}\right\|^{2} &= \left\|\vec{u}\right\|^{2} + \left\|\vec{v}\right\|^{2} - 2\left\|\vec{u}\right\|\left\|\vec{v}\right\|\cos{\theta} \\ \sum_{i = 1}^{n} (u_{i} - v_{i})^{2} &= \sum_{i = 1}^{n} u_{i}^{2} + \sum_{i = 1}^{n} v_{i}^{2} - 2\left\|\vec{u}\right\|\left\|\vec{v}\right\|\cos{\theta} \\ -2\sum_{i = 1}^{n}u_{i}v_{i} &= -2\left\|\vec{u}\right\|\left\|\vec{v}\right\|\cos{\theta} \\ u^{T}v &= \left\|\vec{u}\right\|\left\|\vec{v}\right\|\cos{\theta}\end{aligned}$$

Find the cosine of the angle between each of the following pairs of vectors:

a) $\vec{a}=(3,0), \vec{b}=(3,4)$
b) $\vec{a}=3i+2j, \vec{b}=5i-j$.

---

a) We have

$$\begin{aligned} \vec{a}\cdot \vec{b}&=(3)(3)+(0)(4)=9\\ \left\| \vec { a } \right\| &=\sqrt { { 3 }^{ 2 }+{ 0 }^{ 2 } } =3\\ \left\| \vec { b } \right\| &=\sqrt { { 3 }^{ 2 }+{ 4 }^{ 2 } } =5\\ \Rightarrow \cos\theta &=\frac { \vec { a } \cdot \vec { b } }{ \left\| a \right\| \left\| b \right\| } \qquad (\text{by definition of dot product})\\ &=\frac { 9 }{ 15 }\\ \\ \Rightarrow \theta &\approx{ 53.13 }^{ \circ }. \ _\square \end{aligned}$$

b) We have

$$\begin{aligned} \vec{a}\cdot \vec{b}& =(3i+2j)\cdot (5i-j)\\ &=3(5)+2(-1)\\ &=15-2\\ &=13\\ \\ \left\| \vec { a } \right\| &=\sqrt { { 3 }^{ 2 }+{ 2 }^{ 2 } } \\ &=\sqrt{13}\\ \\ \left\| \vec { b } \right\| &=\sqrt { { 5}^{ 2 }+{ -1 }^{ 2 } } \\ &=\sqrt{26}\\ \\ \Rightarrow \cos\theta &=\frac { \vec { a } \cdot \vec { b } }{ \left\| a \right\| \left\| b \right\| } \qquad (\text{by definition of dot product})\\ &=\frac { 13 }{ \sqrt { 13 } \sqrt { 26 } }\\ &=\frac { 13 }{ 13\sqrt { 2 } } \\ &=\frac { \sqrt { 2 } }{ 2 } \\ \\ \Rightarrow \theta & = { 45 }^{ \circ }. \ _\square \end{aligned}$$

Given two vectors $\vec{v}=4i+3j$ and $\vec{w}=mi+7j$, for what value of $m$ is the angle between them ${ 45 }^{ \circ}?$

---

We have

$$\begin{aligned} \vec{v}\cdot \vec{w} &=(4i+3j)\cdot (mi+7j)\\ &=(4)(m)+(3)(7)\\ &=4m+21\\ \\ \left\| \vec { v } \right\| &=\sqrt { { 4 }^{ 2 }+{ 3 }^{ 2 } } \\ &=5 \\ \\ \left\| \vec { w } \right\| &=\sqrt { { m}^{ 2 }+{ 7 }^{ 2 } } \\ &=\sqrt{m^{2}+49}. \end{aligned}$$

Then from the definition of dot product, we have

$$\begin{aligned} \vec { v } \cdot \vec { w } &=\left\| v \right\| \left\| w \right\| \cos\theta \\ 4m+21&=5\sqrt { { m }^{ 2 }+{ 49 } } \left(\frac { \sqrt { 2 } }{ 2 }\right) \\ 16{ m }^{ 2 }+168m+441&=\frac { 25 }{ 2 } \left({ m }^{ 2 }+49\right) \qquad (\text{both sides squared})\\ 7{ m }^{ 2 }+336m-343&=0\\ (m-1)(m+49)&=0\\ \Rightarrow m&=1 \text{ or } m=-49. \end{aligned}$$

Therefore, for both $m=1$ and $m=-49$, the angle between the two vectors will be ${ 45 }^{ \circ }$. $_\square$