Gabriel's Horn
Gabriel's horn is a shape with the paradoxical property that it has infinite surface area, but a finite volume.
Contents
Construction
Consider the surface area and volume of the solid formed by rotating the region bounded by the \( x\)-axis, \( x =1 \), and \( y = \frac{1}{x} \), around the \( x \)-axis. This solid is called Gabriel's horn.
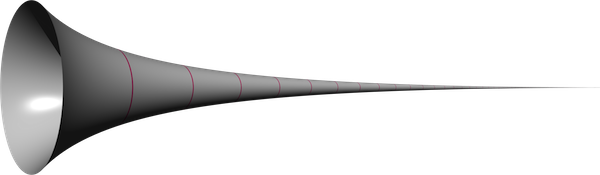
Volume
The volume of the solid of revolution can be found using the disk method:
\[ V = \pi \int_1 ^a \frac{dx}{x^2} = \pi \left( 1 - \frac{1}{a} \right). \]
Now consider what happens as we allow \( a \) to approach infinity:
\[ \displaystyle \lim_{a \to \infty} \pi \left( 1 - \frac{1}{a} \right) = \pi. \]
Surface Area
The surface area of a solid of revolution is given by the formula
\[ S = 2\pi \int_a^b r(x)\sqrt{1+\left( \frac{dy}{dx} \right )^2 } \, dx. \]
In this case, since \( \frac{d}{dx}\left(\frac{1}{x}\right) = -\frac{1}{x^2}, \) that gives us
\[ \begin{align} S &= 2\pi \int_1^a \frac{1}{x} \sqrt{1+\left( -\frac{1}{x^2} \right )^2 } \, dx \\ &= 2\pi \int_1^a \frac{1}{x} \sqrt{1+ \frac{1}{x^4} } \, dx. \end{align}\]
This integral is hard to evaluate, but since in our interval \( \sqrt{1+ \frac{1}{x^4}} \geq 1 \) and \( \frac{1}{x} > 0 \),
\[ 2\pi \int_1^a \frac{1}{x} \sqrt{1+ \frac{1}{x^4} } \, dx \geq 2\pi \int_1^a \frac{1}{x} \, dx. \]
It follows that:
\[ \begin{align} S &\geq 2\pi \int_1^a \frac{1}{x} \, dx \\ S &\geq 2\pi \ln a. \end{align} \]
But \( \displaystyle \lim_{a \to \infty} 2\pi \ln a = \infty \), which means that Gabriel's horn has infinite surface area, but a volume of only \( \pi \)!