General Polygons - Angles

A simple closed figure made up of only line segments is called a polygon. We generally classify polygons according to the number of sides (or vertices) they have. For example, a polygon with 3 sides or vertices is called a triangle; similarly, a polygon with 4 sides or vertices is called a quadrilateral.

A regular polygon is both equiangular and equilateral. For example, a square has sides of equal length and angles of equal measure, and hence it's a regular polygon unlike a rectangle which does not have all sides equal. Similarly, a regular pentagon is a polygon which has all 5 sides equal and has all angles equal.

You must be familiar with the angle sum property of a triangle which states that the sum of the measurements of the three interior angles of a triangle is $180^\circ$.

The sum of the measurements of the three interior angles of a triangle is 180º.

Here's a short diagramatic proof for the above mentioned result:

Now if we consider a quadrilateral, it can be divided into 2 triangles; thus the sum of the measures of the four angles of a quadrilateral is $360^\circ$. Similarly, any $n$-sided polygon can be divided into triangles.

Now, since it can be a tedious job to divide a polygon into many triangles and then calculate the sum of all its angles, we can find the sum $S$ of all the interior angles of any polygon with $n$ sides by the formula

$$S = (n-2) \times 180^\circ.$$

We shall use induction in this proof.

The base case of $n=3$ is true as the sum of the interior angles of a triangle is $180^\circ$ or $\pi$.

Then, assume that the statement is true for $P_k$ $($here $P_k$ denotes a $k$-sided polygon$).$

Now, consider $P_{k+1}$ with vertices $A_1, A_2, \ldots A_k, A_{k+1}$.
Split this polygon into two parts by joining $A_1$ and $A_k$, then

$$\begin{aligned} (\text{Sum of interior angles of } P_{k+1}) &= (\text{Sum of interior angles of } A_1 A_2 \ldots A_{k-1} A_k) + (\text{Sum of interior angles of } A_1 A_k A_{k+1}) \\ &= (k-2)\times 180 ^\circ + 180^\circ \\ &= \big((k+1)-2\big) \times 180^\circ. \end{aligned}$$

This completes the inductive step. $_\square$

On many occasions a knowledge of exterior angles may throw light on the nature of interior angles and sides.

The sum of the measures of the external angles of any polygon is $360^\circ$. This is true whatever the number of sides of the polygon is.

Label the interior angles of $P_n$ as $\text{Int}\angle_1, \text{Int}\angle_2, \ldots, \text{Int}\angle_{n-1}, \text{Int}\angle_n$ and the corresponding exterior angles as $\text{Ext}\angle_1, \text{Ext}\angle_2, \ldots, \text{Ext}\angle_{n-1}, \text{Ext}\angle_n$.

Note that $\text{Int}\angle_i + \text{Ext}\angle_i = 180^\circ, \quad i=1,2, \ldots, n-1,n.$

Then

$$\begin{aligned} (\text{Sum of all exterior angles}) &=n \times 180^\circ - (\text{Sum of all interior angles}) \\ &= n \times 180^\circ - (n-2) \times 180^\circ \\ &= 360^\circ.\ _\square \end{aligned}$$

---

Here's a visual representation of this proof done with the case of a regular decagon.

---

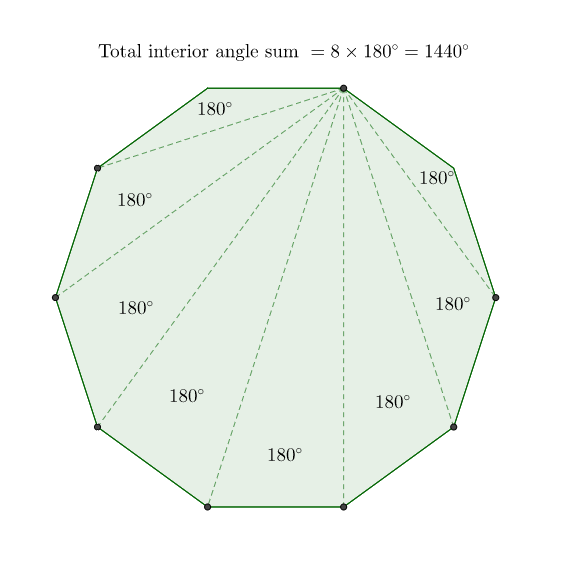
Another short picture-proof without the need of any explanations would be this.

Find the number of sides of a polygon each of whose exterior angles has a measure of $20^\circ$.

---

Total measure of all exterior angles = $360^\circ.$
Measure of each exterior angle = $20^\circ.$
Therefore, the number of exterior angles = $\frac{360^\circ}{20^\circ}$ = $18.$

Thus, the polygon has 18 sides. $_\square$