Genetic Algorithms
A genetic algorithm is an optimisation or search algorithm that works essentially by mimicking the process of evolution.
Contents
Evolution in Nature
Genetic Algorithms are something Computer Science learnt from nature. For a diversion, let us first take a look at how evolution works as proposed by Charles Darwin in his The Origin of Species.
- Traits: Living Creatures consist of data about them encoded in their genetic material (see quine that they carry over to the next generation. This is why the generations are similar.
- Mutation: The replication of the genetic material is not accurate and has a small probability of producing a slightly different code as opposed to what is coded in the genetic material.
- Survival of the Fittest: The mutant variants are usually unlikely to survive. However, what decides whether they survive is in what ways the mutation makes them more fit.
- Natural Selection: Whether a genetic trait survives, not only depends on how fit it is but also non-deterministic factors.
There is an added step that actually heavily contributes towards mutation in sexual reproduction:
- Crossing Over: There is a recombination of genetic material between the two parents that gives rise to the new genetic material
Consider a group of twelve red beetles. They live, let us assume, in some bushes with green leaves. Their population will grow by sexual reproduction, and therefore, can generate variations. Let us imagine also that crows eat these beetles. The more beetles the crows eat, the fewer beetles are available to reproduce. Now, let us think about some different situations that can develop in this beetle population.

In the first situation, a colour variation arises during reproduction, so that there is one beetle that is green in colour instead of red. This beetle, moreover, can pass the colour on to its progeny, so that all its progeny beetles are green. Crows cannot see green-coloured beetles on the green leaves of the bushes, and therefore cannot eat them. What happens then? The progeny of green beetles is not eaten, while the progeny of red beetles continues to be eaten. As a result, there are more and more green beetles than red ones in the beetle population.
In a second situation, again, a colour variation arises during reproduction, but now it results in a beetle that is blue in colour instead of red. This beetle can also pass the colour on to its progeny, so that all its progeny beetles are blue. Crows can see blue-coloured beetles in the green leaves of the bushes as well as they can see red ones, and therefore can eat them. What happens initially? In the population, as it expands, there are a few blue beetles, but most are red. But at this point, an elephant comes by, and stamps on the bushes where the beetles live. This kills most of the beetles. By chance, the few beetles that have survived are mostly blue. The beetle population slowly expands again, but now, the beetles in the population are mostly blue.
It is obvious that in both situations, what started out as a rare variation came to be a common characteristic in the population. In other words, the frequency of an inherited trait changed over generations. Since genes control traits, we can say that the frequency of certain genes in a population changed over generations. This is the essence of the idea of evolution.
But there are interesting differences, too, in the two situations. In the first case, the variation became common because it gave a survival advantage. In other words, it was naturally selected. We can see that the natural selection is exerted by the crows. The more crows there are, the more red beetles would be eaten, and the more the proportion of green beetles in the population would be. Thus, natural selection is directing evolution in the beetle population. It results in adaptations in the beetle population to fit their environment better.
In the second situation, the colour change gave no survival advantage. Instead, it was simply a matter of accidental survival of beetles of one colour that changed the common characteristic of the resultant population. The elephant would not have caused such major havoc in the beetle population if the beetle population had been very large. So, accidents in small populations can change the frequency of some genes in a population, even if they give no survival advantage. This is the notion of genetic drift, which provides diversity without any adaptations.
Now consider a third situation. In this, as the beetle population begins to expand, the bushes start suffering from a plant disease. The amount of leaf material for the beetles is reduced. The beetles are poorly nourished as a result. The average weight of adult beetles decreases from what it used to be when leaves were plentiful, but there is no genetic change occurring. After a few years and a few beetle generations of such scarcity, the plant disease is eliminated. There is a lot of leaf food. At this time, what would we expect the weight of the beetles to be?
Genetic Representation
The first step towards a genetic algorithm is to be able to represent candidate solutions genetically.
Each candidate solution could be termed an individual. Each individual is represented by a chromosome, that is a collection of genes. Genes are variables representing properties of the solution. They could be thought of as decision variables.
There is no fixed approach to do this. It is one of the things on which the efficiency of the algorithm depends.
A very popular genetic representation is a linear array of bits.
In the knapsack problem, each bit could be an indicator of whether we should take the corresponding treasure.
Fitness Function
The fitness function is a mark of the quality of an individual. It is usually positively correlated to the probability of survival and the chance of being selected for a sexual reproduction.
The fitness function is usually modelled by a heuristic that gives the idea of how close the proposed solution is to the optimal solution. Or in cases where the optimal solution has no clear distinction, it merely shows which one is better.
Once again, there is no fixed methods to choose this. Also, this is a very important parameter of the algorithm.
In the knapsack problem, an individual who proposes taking a number of items that is heavier than the capacity of the knapsack receives a fitness of 0.
Otherwise, the fitness is the value of the treasures it takes.
Genetic Operators
Mutation
Usually most of the individual is supposed to be carried forward to the next generation without changes. However, a randomly chosen part of it is changed with a small probability in every generation.
The probability of a gene undergoing mutation could depend on the fitness of the entire individual to which it belongs. Moreover, the distribution could be uniform or non-uniform depending on whether the gene has distinguishing features.
A possible way to mutate a chromosome coded with a linear bit array is to flip a random bit each time.
In case, the solution has got to do something with finding a particular permutation as in this problem, it might make sense to choose two genes and exchange their positions.
Crossover
The crossover is a technique for producing a child solution from more than one parents. It involves recombining genetic data between the two parents.
Here are some ways to do this:
One Point Crossover 
Two Point Crossover 
Cut and Splice 
Uniform Crossover 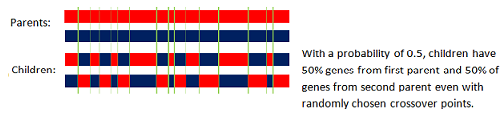
Initialization
Most genetic algorithms are typically initialised with a randomly generated population, i.e, a cluster of individuals. If an heuristic is available, it could be used to generate a population around an area near which the optimal solution is probable.
The size of the population is usually huge, comprising thousands of individuals. However, it actually depends on the search space of the problem.
The Loop
The key idea is to carry on the process of evolution generation after generation using the reproduction techniques mentioned above. The algorithm could be designed to terminate when one or more of the following occurs:
- A Provably Optimal solution is found
- A very high quality solution is found
- The fitness of the individuals no longer improve
- A fixed number of generations have reached
Applications
\[ \begin{array} { l l l l l l l l l } & & S & T & I & R & L & I & N & G \\ +& G & A & L & L & I & P & O & L & I \\ \hline & P & R & O & T & O & S & T & A & R \\ \hline \end{array} \]
In the cryptarithm above, each letter represents a unique digit.
Find the value of \(\overline{\text{GALOISRATS}}\)
Read an interesting note on cryptarithms here