Principal Component Analysis
Contents
- Introduction
- Setup
- The General PCA Subspace
- The Setup
- From Approximate Equality to Minimizing Function
- Deriving Principal Component Spanning Vectors
- Data Points, Data Vectors
- The First Principal Component: the Setup
- The First Principal Component: the Derivation
- Deriving the Second, Third, ... Principal Components
Introduction
Many of today's popular data types--like images, documents from the web, genetic data, consumer information--are often very "high-dimensional." By high-dimensional we mean that each piece of data consists of many many individual pieces or coordinates. For example, take a grayscale digital image like the one shown in the image below. Such an image is made up of many small squares called "pixels," each of which has a brightness level between 0 (completely black) and 255 (completely white). In other words, a grayscale digital image can be thought of as a matrix whose \(\left(i,j\right)^\text{th}\) value is equal to the brightness level of the \(\left(i,j\right)^\text{th}\) pixel in the image. (A color image is then just a set of three such matrices, one for each color channel red, green, and blue.) In a megapixel grayscale image, not too large by today's standards, there are one million pixels/brightness values--this makes such an image one-million-dimensional datapoint (having one dimension for each of its one million pixels).
![]()
This high dimensionality makes performing standard machine learning tasks like face recognition--or the problem of identifying the identity of a person from an image--directly on the image itself computationally intractable, as the number of calculations involved with such a task typically grows at least quadratically with the dimension of the data (see e.g., Newton's method). Because of this property, reducing the dimension of data prior to processing is often a crucial step to making efficient machine learning algorithms.
Setup
One standard way of reducing the dimension of a data is called principal component analysis (or PCA for short). Geometrically speaking, PCA reduces the dimension of a dataset by squashing it onto a proper lower-dimensional line (or more generally a hyperplane, also often referred to as a subspace) which retains as much of the original data’s defining characteristics as possible.
The gist of this idea is illustrated with a two-dimensional toy data set shown in the image below, with the two-dimensional data squashed (or projected) onto a proper one-dimensional line that retains much of the shape of the original data. In other words, the dimension of the dataset has been reduced from two to one: a 50% reduction. In practice this amount is typically much greater; for example, it is quite common for face recognition tasks to reduce images to 1% or less of their original dimension.
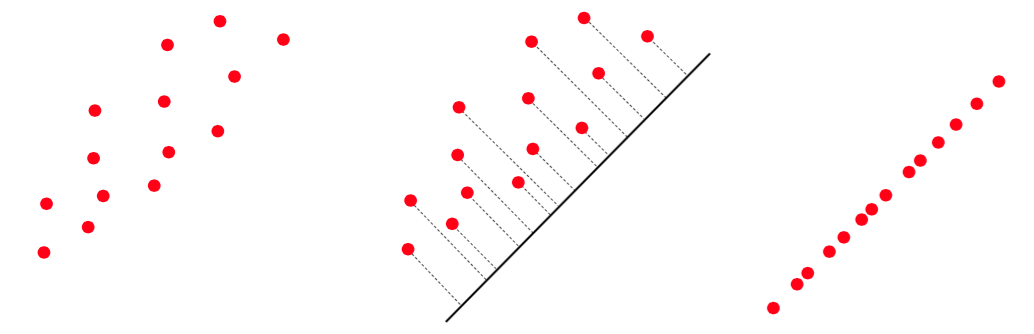
How do we find the PCA subspace? In short, we can set up a problem that, when properly solved, recovers a spanning set or a collection of vectors which spans the proper subspace. To see how this is done, all we need to do is follow our nose and begin by writing out our goal with PCA more formally.
So, first let us say that we have \(P\) data points \(\mathbf{x}{}_{1}...\mathbf{x}_{P}\), each a vector of dimension \(N\). Expressing our goal with PCA more formally, we want to determine a good \(K(<N)\)-dimensional subspace that represents the data well \((\)the value of \(K\) is typically chosen according to computational limitations or via a skree plot{[}red link{]}\().\) Remember from {[}red link linear algebra{]} that in \(N\)-dimensional space any \(K\)-dimensional subspace is spanned by \(K\) linearly independent vectors, which we will denote as \(\mathbf{c}_{1}...\mathbf{c}_{K}\) \((\)note these are also length \(N\) vectors as well\().\) In other words, any point \(\mathbf{x}\) in this subspace can be defined by a linear combination of the spanning vectors as
\[\begin{equation} \underset{k=1}{\overset{K}{\sum}}\mathbf{c}_{k}w_{k}=\mathbf{x}, \end{equation}\]
where the exact value of the weights \(w_{1},...,w_{K}\) is dependent on the particular \(\mathbf{x}\) chosen. With this in mind, how can we formally express the goal of PCA?
Well, suppose our dataset is in fact represented very well by the subspace spanned by a particular set of vectors \(\mathbf{c}_{1},...,\mathbf{c}_{K}\). Formally, then, if our \(p^\text{th}\) data point lies approximately in the span of \(\mathbf{c}_{1},...,\mathbf{c}_{K},\) we have that
\[\begin{equation} \underset{k=1}{\overset{K}{\sum}}\mathbf{c}_{k}w_{k,p}\approx\mathbf{x}_{p}, \end{equation}\]
where the weights \(w_{1,p},...,w_{K,p}\) are tuned specifically for the point \(\mathbf{x}_{p}\) and \(\approx\) is interpreted somewhat loosely \((\)as if \(\mathbf{x}_{p}\) lies approximately in this span\().\) Saying that all \(P\) points lie approximately in this span then means that the above holds for all \(p\).
As a quick example, in the image below, we show a prototype of PCA dimension reduction applied to the task of face recognition. Here, given a database of known individuals, where each input data \(\mathbf{x}_{p}\) is a facial image, we apply PCA to lower the dimension of the database. As shown in the figure, since the data itself consists of facial images, the spanning vectors will tend to look like (rather ghostly) "basis faces."

Pictures of a single individual in the database will tend to cluster together in the lower dimensional PCA subspace, all being represented primarily by a few of the same basis faces. This means that the entire database itself--consisting of images of various people--will tend to look like a collection of fairly distinct clusters of points on our PCA subspace. To recognize the individual in a new picture, we then project the new image down onto the learned PCA subspace and identify the individual by simply finding the closest cluster of projected facial images from our database and assigning the associated identity to the person in the new image.
The General PCA Subspace
How do we find a set of \(K\) spanning vectors for our desired subspace? There are several ways. In this section, we formulate a numerical optimization problem that, when solved, provides some set of spanning vectors for the desired subspace. In the section that follows, we derive a classic set of spanning vectors--known as principal components--which can be solved for "in closed form."
The Setup
Note that by stacking the spanning vectors column-wise into an \(N\times K\) matrix \(\mathbf{C}\) as \(\mathbf{C}=\left[\mathbf{c}_{1}\vert\mathbf{c}_{2}\vert\cdot\cdot\cdot\vert\mathbf{c}_{K}\right]\) and by denoting \(\mathbf{w}_{p}=\left[\begin{array}{cccc} w_{1,p} & w_{2,p} & \cdots & w_{K,p}\end{array}\right]^{T}\) we can write \(\sum_{k=1}^{K}\mathbf{c}_{k}w_{k,p}=\mathbf{C}\mathbf{w}_{p}\). With this notation the previous equation can then be written more compactly: \(\mathbf{C}\mathbf{w}_{p}\approx\mathbf{x}_{p}\).
Now that we know what we ideally want---namely, a) a set of vectors \(\mathbf{c}_{1},...,\mathbf{c}_{K}\) that spans a \(K\)-dimensional subspace on which our dataset approximately lies and b) proper weights \(w_{k,p}\) for each spanning vector-datapoint pair--how do we actually find them? Let's follow our nose a bit further.
From Approximate Equality to Minimizing Function
Notice that if we have a good spanning set and weights, then the relationship for PCA holding for the \(p^\text{th}\) point means that the squared distance between \(\mathbf{C}\mathbf{w}_{p}\) and \(\mathbf{x}_{p}\) should be quite small. In other words, the value
\[\begin{equation} \left\Vert \mathbf{C}\mathbf{w}_{p}-\mathbf{x}_{p}\right\Vert _{2}^{2} \end{equation}\]
should be minimal (given indeed that the spanning vectors are linearly independent). In fact, if it is true that all of our \(P\) points lie close to the subspace, then the sum of these values over the dataset should be small as well; that is,
\[\begin{equation} g=\underset{p=1}{\overset{P}{\sum}}\left\Vert \mathbf{C}\mathbf{w}_{p}-\mathbf{x}_{p}\right\Vert _{2}^{2} \end{equation}\]
should be minimal as well. In other words, a great set of values for our spanning set and corresponding weights minimizes the above quantity, which we can also refer to as a multivariable function \(g\). Although it may seem that we have simply phrased in a slightly different way, we have actually made a crucial step here. This is because we no longer need to assume that we have the proper spanning set and weights: if we can minimize the quantity in the equation above, assuming the spanning vectors are linearly independent, we have indeed found them. In fact, many problems in machine learning take the form of a minimization problem--including linear regression, logistic regression, and neural networks--and some problems like \(k\)-means clustering even aim to minimize an extremely similar function.
And we can solve this problem--an entire field of study known as mathematical or nonlinear optimization focuses precisely on methods for minimizing such multivariable functions. Any set of spanning vectors returned by minimizing the above technically defines a PCA subspace.
Deriving Principal Component Spanning Vectors
Here, we derive a classic set of "principal component" spanning vectors, which can be computed in closed form and, in addition to being linearly independent, are actually orthonormal [link] as well (that is, they are all perpendicular to each other and have unit length). This is done by deriving one principal component vector at a time--from the most to least representative of the dataset. However, note that while these spanning vectors can be derived in "closed form," they still require considerable computation to employ in practice.
Data Points, Data Vectors
The derivation of each principal component spanning vectors results from thinking of our datapoints as vectors. Remember we can always switch back and forth in our minds between thinking of a "point" equivalently as a vector, or an arrow stemming from the origin whose head lies precisely where the point does. This is illustrated with a toy dataset in the picture below, where for simplicity the data is assumed to be centered at the origin. We will assume our data is origin-centered here--this will just simplify the calculations that follow and will not affect the final results. Moreover, this is usually done in practice prior to performing PCA anyway.

Thinking of a set of origin-centered points (left panel) as a set of vectors (middle and right panels--note in both that the origin is shown as a large black dot from which the vectors stem for visualization purposes only) motivates the search for principal component spanning vectors (as those which highly correlate with the data). In the right panel, the two dotted black arrows are the first and second principal components of the data, \(\mathbf{c}_{1}\) and \(\mathbf{c}_{2},\) respectively. Here the first component is drawn longer for visualization purposes only.
Now that we are thinking in terms of vectors, let's reason out the value of the first principal component, or the spanning vector of our ideal subspace. This should be the unit length (spanning) that determines a line about which our data is the most spread out or, in other words, the one that generally aims in the same direction as our data vectors.
The First Principal Component: the Setup
Take the trivial example of a single data vector \(\mathbf{x}\), as illustrated in the picture below; we can tell if a spanning vector \(\mathbf{c}_{1}\) generates such a line for \(\mathbf{x}\) if \(\mathbf{c}_{1}\) or \(-\mathbf{c}_{1}\) lies in the same direction as \(\mathbf{x}\). Mathematically speaking, we can tell if this is indeed the case if the inner product between the two vectors \(\mathbf{x}^{T}\mathbf{c}_{1}\) or if \(\mathbf{x}^{T}\left(-\mathbf{c}_{1}\right)\) is as large and positive (the former indicating that \(\mathbf{c}_{1}\) points in the direction of \(\mathbf{x}\), while the latter indicating -\(\mathbf{c}_{1}\) does). Combining these two possibilities, we can then say that the unit length \(\mathbf{c}_{1}\) generates a representative line for the vector \(\mathbf{x}\) if \(\left(\mathbf{x}^{T}\mathbf{c}_{1}\right)^{2}\) is large (it is always positive).
(left panel) A vector \(\mathbf{c}_{1}\) points in the direction of a data vector \(\mathbf{x},\) and the inner product \(\mathbf{x}^{T}\mathbf{c_{1}}\) is large and positive.
(middle panel) Likewise, this is a case where \(-\mathbf{c}_{1}\) points in the direction of \(\mathbf{x}\) and \(\mathbf{x}^{T}\left(-\mathbf{c}_{1}\right)\) is large and positive.
(right panel) The case with \(P\) data vectors holds analogously (see text for further details).
Analogously, \(\mathbf{c}_{1}\) generates a representative line for \(P\) data vectors \(\mathbf{x}_{1},...,\mathbf{x}_{P}\) when the total squared inner product against the data
\[\begin{equation} \underset{p=1}{\overset{P}{\sum}}\left(\mathbf{x}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2} \end{equation}\]
is large, and the larger the better. In fact, we want this to be as large as possible, since the larger its value the better the line generated by \(\mathbf{c}_{1}\) captures the spread of the dataset. So, how do we determine the \(\mathbf{c}_{1}\) that maximizes this quantity?
The First Principal Component: the Derivation
Here comes the math. Let's rewrite the equation above--this will help tease out the answer. Denote by \(\mathbf{X}\) the \(N\times P\) matrix formed by stacking the data vectors columnwise as \(\mathbf{X}=\left[\begin{array}{cccc} \mathbf{x}_{1} & \mathbf{x}_{2} & \cdots & \mathbf{x}_{P}\end{array}\right]\). Then the above can be written equivalently as
\[\begin{equation} \underset{p=1}{\overset{P}{\sum}}\left(\mathbf{x}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}=\Vert\mathbf{X}^{T}\mathbf{c}_{1}\Vert_{2}^{2}=\mathbf{c}_{1}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{c}_{1}^{\,}. \end{equation}\]
Here's where we need a fundamental fact from linear algebra known as the eigenvalue decomposition of a matrix or, likewise, the spectral theorem of symmetric matrices. Using this fact, we can decompose the matrix \(\mathbf{X}\mathbf{X}^{T}\) as \(\mathbf{X}\mathbf{X}^{T}=\underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\mathbf{e}_{p}^{\,}\mathbf{e}_{p}^{T},\) where each \(d_{p}\) is a real eigenvalue, \(d_{1}\geq d_{2}\geq\cdots\geq d_{P}\), and the set of \(N\times1\) eigenvectors \(\mathbf{e}_{1},...,\mathbf{e}_{P}\) are orthonormal (that is, orthogonal and of unit length). Replacing \(\mathbf{X}\mathbf{X}^{T}\) with this eigendecomposition in the equation above, we then have equivalently that
\[\begin{equation} \mathbf{c}_{1}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{c}_{1}^{\,}=\mathbf{c}_{1}^{T}\left(\underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\mathbf{e}_{p}^{\,}\mathbf{e}_{p}^{T}\right)\mathbf{c}_{1}^{\,}=\underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\mathbf{c}_{1}^{T}\mathbf{e}_{p}^{\,}\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}=\underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}. \end{equation}\]
Now, since \(d_{1}\) is the largest eigenvalue, we can see that it must be the smallest upper bound possible on this quantity since
\[\begin{equation} \underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}\leq\underset{p=1}{\overset{P}{\sum}}d_{1}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}=d_{1}^{\,}\underset{p=1}{\overset{P}{\sum}}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}=d_{1}^{\,}. \end{equation}\]
Here the last equality follows from the fact that the eigenvectors form a basis over which we may decompose \(\mathbf{c}_{1}\) as \(\mathbf{c}_{1}=\underset{p=1}{\overset{P}{\sum}}\alpha_{p}\mathbf{e}_{p}\) and hence \(\alpha_{p}=\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\), and since \(\mathbf{c}_{1}\) has unit length by assumption we have that \(\left\Vert \mathbf{c}_{1}\right\Vert _{2}^{2}=\sum_{p=1}^{P}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}=1\).
Now, since \(\mathbf{c}_{1}\) as well as the eigenvectors are all unit length, if we set \(\mathbf{c}_{1}=\mathbf{e}_{1},\) we can actually achieve this upper bound \(\big(\)since the eigenvectors are orthonormal, i.e. \(\mathbf{e}_{p}^{T}\mathbf{e}_{1}^{\,}=0\) when \(p\neq1,\) and \(\mathbf{e}_{p}^{T}\mathbf{e}_{1}^{\,}=1\) when \(p=1\big)\) since we have
\[\begin{equation} \underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{1}^{\,}\right)^{2}=\underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{e}_{1}^{\,}\right)^{2}=d_{1}^{\,}. \end{equation}\]
Therefore, the first principal component is \(\mathbf{c}_{1}=\mathbf{e}_{1}\), i.e. the eigenvector associated with the largest eigenvalue of the matrix \(\mathbf{X}\mathbf{X}^{T}\).
Deriving the Second, Third, ... Principal Components
Deriving the additional principal components follows by induction in a manner very much analogous with the derivation of the first. That is, suppose we have derived the first \(k-1\) principal components as the \(k-1\) eigenvectors associated with the \(k-1\) largest eigenvalues of the matrix \(\mathbf{X}\mathbf{X}^{T}\). We then want to show that the \(k^\text{th}\) principal component \(\mathbf{c}_{k}\) is the eigenvector of \(\mathbf{X}\mathbf{X}^{T}\) associated with the \(k^\text{th}\) largest eigenvalue.
In order to do this, we again use the eigen-decomposition of \(\mathbf{X}\mathbf{X}^{T}\) in order to write the above as
\[\begin{equation} \mathbf{c}_{k}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{c}_{k}^{\,}=\underset{p=1}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{k}^{\,}\right)^{2}=\underset{p=k}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{k}^{\,}\right)^{2}, \end{equation}\]
where the last equality holds because \(\mathbf{c}_{k}\) is assumed perpendicular to the first \(k-1\) principal components. Following the argument for the first principal component, here again we can derive an upper bound on the above as
\[ \underset{p=k}{\overset{P}{\sum}}d_{p}^{\,}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{k}^{\,}\right)^{2}\leq d_{k}\underset{p=k}{\overset{P}{\sum}}\left(\mathbf{e}_{p}^{T}\mathbf{c}_{k}^{\,}\right)\leq d_{k} \]
and complete the proof by again noting that we can meet the upper bound by setting \(\mathbf{c}_{k}=\mathbf{e}_{k}\).