Problem solving - charges and fields

A spherical shell of uniform charge density σ has a circular hole cut out of it as shown below:

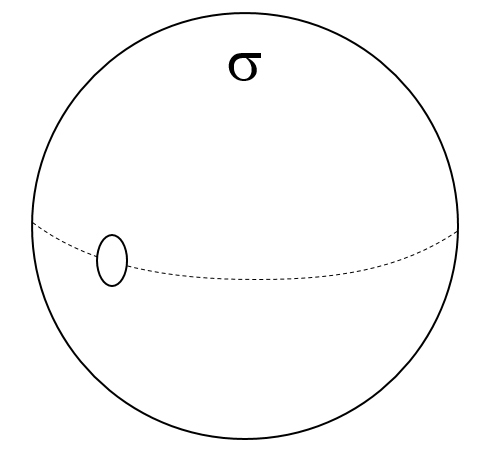
What is the Electric Field at a radius just outside the sphere, directly over the center of the circular, cut-out hole?

HINT: the hole is small enough that you can treat it as flat, and the point at which you are calculating the field is so close to the hole that it can be approximated as an infinite plane.

Two charges are on the $x$-axis. One of them is a $9\text{ C}$ charge located at $x = 0\text{ m}$. The other is a $1\text{ C}$ charge located at $x = 1\text{ m}$. Find the location on the $x$-axis where the net electric field due to these charges is $0 \text{ N/C}$.

An infinite number of charges each of magnitude $q$ are placed on the $x$-$\text {axis}$ at the distance of $1,2,4,8,16,\ldots$ $\text{m}$ respectively. Find the intensity of electric field at the origin.

If the intensity can be expressed in the form $\dfrac { q }{ n\pi { \varepsilon }_{ o } }$, find $\Gamma (n+1)$.

• Assume the medium to be vacuum.

• Here, $\Gamma (n)$ and ${ \varepsilon }_{ o }$ represent the Gamma function and permittivity of free space respectively.

A bumble bee charged to $1 \text{ C}$ flies from $(0 \text{ m}, 0\text{ m})$ to $(1 \text{ m}, 1\text{ m})$ through a region with electric field $\vec{E}=(\hat{x}+\hat{y})\dfrac{N}{C}$. Find the work done by the electric field on the bumble bee.

A non-conducting solid sphere has volume charge density that varies as $\rho ={ \rho }_{ 0 }r$ where ${ \rho }_{ 0 }$ is a constant and $r$ is distance from center. Find out electric field intensities at $r<R$, where $R$ is the radius of sphere.

Given,

$R$= 4 meter

$r$= 2 meter

${ \rho }_{ 0 }$= $8.854\times { 10 }^{ -11 }$

More questions