Recurrent Neural Network
 A simple recurrent neural network
A simple recurrent neural network
Recurrent neural networks are artificial neural networks where the computation graph contains directed cycles. Unlike feedforward neural networks, where information flows strictly in one direction from layer to layer, in recurrent neural networks (RNNs), information travels in loops from layer to layer so that the state of the model is influenced by its previous states. While feedforward neural networks can be thought of as stateless, RNNs have a memory which allows the model to store information about its past computations. This allows recurrent neural networks to exhibit dynamic temporal behavior and model sequences of input-output pairs.
Because they can model temporal sequences of input-output pairs, recurrent neural networks have found enormous success in natural language processing (NLP) applications. This includes machine translation, speech recognition, and language modeling. RNNs have also been used in reinforcement learning to solve very difficult problems at a level better than humans. A recent example is AlphaGo, which beat world champion Go player Lee Sedol in 2016. An interactive example of an RNN for generating handwriting samples can be found here.
Contents
Problems with Modeling Sequences
Consider an application that needs to predict an output sequence \(y = \left(y_1, y_2, \dots, y_n\right)\) for a given input sequence \(x = \left(x_1, x_2, \dots, x_m\right)\). For example, in an application for translating English to Spanish, the input \(x\) might be the English sentence \(\text{"i like pizza"}\) and the associated output sequence \(y\) would be the Spanish sentence \(\text{"me gusta comer pizza"}\). Thus, if the sequence was broken up by character, then \(x_1=\text{"i"}\), \(x_2=\text{" "}\), \(x_3=\text{"l"}\), \(x_4=\text{"i"}\), \(x_5=\text{"k"}\), all the way up to \(x_{12}=\text{"a"}\). Similarly, \(y_1=\text{"m"}\), \(y_2=\text{"e"}\), \(y_3=\text{" "}\), \(y_4=\text{"g"}\), all the way up to \(y_{20}=\text{"a"}\). Obviously, other input-output pair sentences are possible, such as \((\text{"it is hot today"}, \text{"hoy hace calor"})\) and \((\text{"my dog is hungry"}, \text{"mi perro tiene hambre"})\).
It might be tempting to try to solve this problem using feedforward neural networks, but two problems become apparent upon investigation. The first issue is that the sizes of an input \(x\) and an output \(y\) are different for different input-output pairs. In the example above, the input-output pair \((\text{"it is hot today"}, \text{"hoy hace calor"})\) has an input of length \(15\) and an output of length \(14\) while the input-output pair \((\text{"my dog is hungry"}, \text{"mi perro tiene hambre"})\) has an input of length \(16\) and an output of length \(21\). Feedforward neural networks have fixed-size inputs and outputs, and thus cannot be automatically applied to temporal sequences of arbitrary length.
The second issue is a bit more subtle. One can imagine trying to circumvent the above issue by specifying a max input-output size, and then padding inputs and outputs that are shorter than this maximum size with some special null character. Then, a feedforward neural network could be trained that learns to produce \(y_i\) on input \(x_i\). Thus, in the example \((\text{"it is hot today"}, \text{"hoy hace calor"})\), the training pairs would be
\[\big\{(x_1=\text{"i"}, y_1=\text{"h"}), (x_2=\text{"t"}, y_2=\text{"o"}), \dots, (x_{14}=\text{"a"}, y_{14}=\text{"r"}), (x_{15}=\text{"y"}, x_{15}=\text{"*"})\big\},\]
where the maximum size is \(15\) and the padding character is \(\text{"*"}\), used to pad the output, which at length \(14\) is one short of the maximum length \(15\).
The problem with this is that there is no reason to believe that \(x_1\) has anything to do with \(y_1\). In many Spanish sentences, the order of the words (and thus characters) in the English translation is different. Thus, if the first word in an English sentence is the last word in the Spanish translation, it stands to reason that any network that hopes to perform the translation will need to remember that first word (or some representation of it) until it outputs the end of the Spanish sentence. Any neural network that computes sequences needs a way to remember past inputs and computations, since they might be needed for computing later parts of the sequence output. One might say that the neural network needs a way to remember its context, i.e. the relation between its past and its present.
Recurrent Neural Networks
Both of the issues outlined in the above section can be solved by using recurrent neural networks. Recurrent neural networks, like feedforward layers, have hidden layers. However, unlike feedforward neural networks, hidden layers have connections back to themselves, allowing the states of the hidden layers at one time instant to be used as input to the hidden layers at the next time instant. This provides the aforementioned memory, which, if properly trained, allows hidden states to capture information about the temporal relation between input sequences and output sequences.
RNNs are called recurrent because they perform the same computation (determined by the weights, biases, and activation functions) for every element in the input sequence. The difference between the outputs for different elements of the input sequence comes from the different hidden states, which are dependent on the current element in the input sequence and the value of the hidden states at the last time step.
In simplest terms, the following equations define how an RNN evolves over time:
\[\begin{align} o^t &= f\big(h^t; \theta\big)\\ h^t &= g\big(h^{t-1}, x^t; \theta\big), \end{align}\]
where \(o^t\) is the output of the RNN at time \(t,\) \(x^t\) is the input to the RNN at time \(t,\) and \(h^t\) is the state of the hidden layer(s) at time \(t.\) The image below outlines a simple graphical model to illustrate the relation between these three variables in an RNN's computation graph.
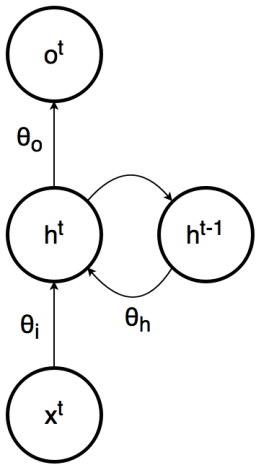 A graphical model for an RNN. The values \(\theta_i\), \(\theta_h\), and \(\theta_o\) represent the parameters associated with the inputs, previous hidden layer states, and outputs, respectively.
A graphical model for an RNN. The values \(\theta_i\), \(\theta_h\), and \(\theta_o\) represent the parameters associated with the inputs, previous hidden layer states, and outputs, respectively.
The first equation says that, given parameters \(\theta\) (which encapsulates the weights and biases for the network), the output at time \(t\) depends only on the state of the hidden layer at time \(t\), much like a feedforward neural network. The second equation says that, given the same parameters \(\theta\), the hidden layer at time \(t\) depends on the hidden layer at time \(t-1\) and the input at time \(t\). This second equation demonstrates that the RNN can remember its past by allowing past computations \(h^{t-1}\) to influence the present computations \(h^{t}\).
Thus, the goal of training the RNN is to get the sequence \(o^{t+\tau}\) to match the sequence \(y_t\), where \(\tau\) represents the time lag \((\)it's possible that \(\tau=0)\) between the first meaningful RNN output \(o^{\tau + 1}\) and the first target output \(y_t\). A time lag is sometimes introduced to allow the RNN to reach an informative hidden state \(h^{\tau + 1}\) before it starts producing elements of the output sequence. This is analogous to how humans translate English to Spanish, which often starts by reading the first few words in order to provide context for translating the rest of the sentence. A simple case when this is actually required is when the last word in the input sequence corresponds to the first word in the output sequence. Then, it would be necessary to delay the output sequence until the entire input sequence is read.
Unrolling RNNs
RNNs can be difficult to understand because of the cyclic connections between layers. A common visualization method for RNNs is known as unrolling or unfolding. An RNN is unrolled by expanding its computation graph over time, effectively "removing" the cyclic connections. This is done by capturing the state of the entire RNN (called a slice) at each time instant \(t\) and treating it similar to how layers are treated in feedforward neural networks. This turns the computation graph into a directed acyclic graph, with information flowing in one direction only. The catch is that, unlike a feedforward neural network, which has a fixed number of layers, an unfolded RNN has a size that is dependent on the size of its input sequence and output sequence. This means that RNNs designed for very long sequences produce very long unrollings. The image below illustrates unrolling for the RNN model outlined in the image above at times \(t-1\), \(t\), and \(t+1\).
 An unfolded RNN at time steps \(t-1\), \(t\), and \(t+1\).
An unfolded RNN at time steps \(t-1\), \(t\), and \(t+1\).
One thing to keep in mind is that, unlike a feedforward neural network's layers, each of which has its own unique parameters (weights and biases), the slices in an unrolled RNN all have the same parameters \(\theta_i\), \(\theta_h\), and \(\theta_o\). This is because RNNs are recurrent, and thus the computation is the same for different elements of the input sequence. As mentioned earlier, the differences in the output sequence arise from the context preserved by the previous, hidden layer state \(h^{t-1}\).
Furthermore, while each slice in the unrolling may appear to be similar to a layer in the computation graph of a feedforward graph, in practice the variable \(h^t\) in an RNN can have many internal hidden layers. This allows the RNN to learn more hierarchal features since a hidden layer's feature outputs can be another hidden layer's inputs. Thus, each variable \(h^t\) in the unrolling is more akin to the entirety of hidden layers in a feedforward neural network. This allows RNNs to learn complex "static" relationships between the input and output sequences in addition to the temporal relationship captured by cyclic connections.
Backpropagation through Time (BPTT)
Training recurrent neural networks is very similar to training feedforward neural networks. In fact, there is a variant of the backpropagation algorithm for feedforward neural networks that works for RNNs, called backpropagation through time (often denoted BPTT). As the name suggests, this is simply the backpropagation algorithm applied to the RNN backwards through time.
Backpropagation through time works by applying the backpropagation algorithm to the unrolled RNN. Since the unrolled RNN is akin to a feedforward neural network with all elements \(o_t\) as the output layer and all elements \(x_t\) from the input sequence \(x\) as the input layer, the entire input sequence \(x\) and output sequence \(o\) are needed at the time of training.
BPTT starts similarly to backpropagation, calculating the forward phase first to determine the values of \(o_t\) and then backpropagating (backwards in time) from \(o_t\) to \(o_1\) to determine the gradients of some error function with respect to the parameters \(\theta\). Since the parameters are replicated across slices in the unrolling, gradients are calculated for each parameter at each time slice \(t\). The final gradients output by BPTT are calculated by taking the average of the individual, slice-dependent gradients. This ensures that the effects of the gradient update on the outputs for each time slice are roughly balanced.
Vanishing/Exploding Gradients Problem
One issue with RNNs in general is known as the vanishing/exploding gradients problem. This problem states that, for long input-output sequences, RNNs have trouble modeling long-term dependencies, that is, the relationship between elements in the sequence that are separated by large periods of time.
For example, in the sentence \(\text{"The quick brown fox jumped over the lazy dog"}\), the words \(\text{"fox"}\) and \(\text{"dog"}\) are separated by a large amount of space in the sequence. In the unrolling of an RNN for this sequence, this would be modeled by a large difference \(\Delta t\) in the time \(x_a\) for the start of the word \(\text{"fox"}\) and \(x_a + \Delta t\) for the end of the word \(\text{"dog"}\). Thus, if an RNN was attempting to learn how to identify subjects and objects in sentences, it would need to remember the word \(\text{"fox"}\) (or some hidden state representing it), the subject, up until it reads the word \(\text{"dog"}\), the object. Only then would the RNN be able to output the pair \((\text{"fox"}, \text{"dog"})\), having finally identified both a subject and an object.
This problem arises due to the use of the chain rule in the backpropagation algorithm. The actual proof is a bit messy, but the idea is that, because the unrolled RNN for long sequences is so deep and the chain rule for backpropagation involves the products of partial derivatives, the gradient at early time slices is the product of many partial derivatives. In fact, the number of factors in the product for early slices is proportional to the length of the input-output sequence. This is a problem because, unless the partial derivatives are all close in value to \(1\), their product will either become very small, i.e. vanishing, when the partial derivatives are \(\lt 1\), or very large, i.e. exploding, when the partial derivatives are \(\gt 1\). This causes learning to become either very slow (in the vanishing case) or wildly unstable (in the exploding case).
Long Short-term Memory
Luckily, recent RNN variants such as LSTM (Long Short-Term Memory) have been able to overcome the vanishing/exploding gradient problem, so RNNs can safely be applied to extremely long sequences, even ones that contain millions of elements. In fact, LSTMs addressing the gradient problem have been largely responsible for the recent successes in very deep NLP applications such as speech recognition, language modeling, and machine translation.
LSTM RNNs work by allowing the input \(x_t\) at time \(t\) to influence the storing or overwriting of "memories" stored in something called the cell. This decision is determined by two different functions, called the input gate for storing new memories, and the forget gate for forgetting old memories. A final output gate determines when to output the value stored in the memory cell to the hidden layer. These gates are all controlled by the current values of the input \(x_t\) and cell \(c_t\) at time \(t\), plus some gate-specific parameters. The image below illustrates the computation graph for the memory portion of an LSTM RNN (i.e. it does not include the hidden layer or output layer).
 Computation graph for an LSTM RNN, with the cell denoted by \(c_t\). Note that, in this illustration, \(o_t\) is not the output of the RNN, but the output of the cell to the hidden layer \(h_t\).[1]
Computation graph for an LSTM RNN, with the cell denoted by \(c_t\). Note that, in this illustration, \(o_t\) is not the output of the RNN, but the output of the cell to the hidden layer \(h_t\).[1]
While the general RNN formulation can theoretically learn the same functions as an LSTM RNN, by constraining the form that memories can take and how they are modified, LSTM RNNs can learn long-term dependencies quickly and stably, and thus are much more useful in practice.
References
- , B. Long_Short_Term_Memory. Retrieved October 4, 2015, from https://commons.wikimedia.org/wiki/File:Long_Short_Term_Memory.png