Reflection
As light reflects from mirrors, we reflect lines and graphs from mirrors in mathematics. Reflections are of great interest in mathematics as they can be used in different areas of geometry to prove many results. In calculus and analysis, there are terms which make use of reflection like even and odd functions, inverse of a function, etc.

Definition
The reflection of a point, line, or a figure is the mirrored image of it along some line, plane, etc.
For example, in two dimensions, reflecting a line over another line results in a second line. In the figure below, the line \(y=3x\) is reflected over the line \(y=x\), resulting in the line \(y=\frac{x}{3}.\)
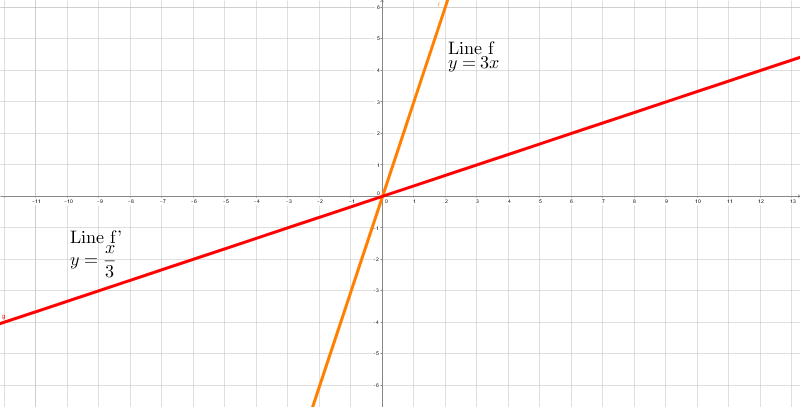
Construction
In practical applications, it is sometimes necessary to construct the reflections of points, lines, and even polygons about a line.
One method of doing it is via a compass. The details of this construction are given below.
Reflection of a given point \(A\) about a given line \(l:\)
- Choose any two points on \(l\) \((\)say \(O_1\) and \(O_2).\)
- Draw two circles centered at \(O_1\) and \(O_2\) such that each circle passes through the common point \(A.\)
- Now, call the other intersection point of the two circles \(B.\)
- Then, \(B\) is the reflection of \(A\) about \(l\).
Construction of Image
A proof of this is given below.
If we show that the line joining \(A\) and \(B\) is perpendicular to \(l\) and that these points are equidistant from \(l,\) then we're done!
So, let's join \(A\) and \(B\). Let \(AB\) intersect \(l\) at \(O\).
Note that as \(A\) and \(B\) both lie on the circles with centers \(O_1\) and \(O_2\), we have
\[ O_1A=O_1B, \quad O_2A=O_2B.\]
As \(O_1O_2=O_1O_2,\) we see that
\[\Delta O_1O_2A \cong \Delta O_1O_2B.\]
Hence \(\angle O_1O_2A=\angle O_1O_2B\). Also, as \(O_2A=O_2B\) and \(OO_2=OO_2,\) we have
\[\begin{align} \Delta OO_2A &\cong \Delta OO_2B \\ \Rightarrow OA&=OB \\ \Rightarrow \angle AOO_2 &= \angle BOO_2. \end{align}\]
As \(\angle AOO_2\) and \(\angle BOO_2\) are angles on a straight line, \(\angle AOO_2+\angle BOO_2 = 180^\circ. \)
Hence we conclude that \(\angle AOO_2=\angle BOO_2=90^\circ\). This means that the distance of \(A\) from \(l\) is \(OA\). Similarly the distance of \(B\) from \(l\) is \(OB\). As \(OA=OB\), both \(A\) and \(B\) are equidistant from the line \(l\).
So, we're done! \(_\square\)
Some miscellaneous constructions are as follows:
- To reflect a line \((\)say \(l')\) about another line \(l\), choose any two points on the line and reflect it about \(l\). Join the reflections to get the reflected line.
- To reflect a line segment about a line, reflect the endpoints of the segment and join them.
- To reflect a polygon about a line, reflect the line segments.
Reflection Across a Line
While reflecting a point about the \(x\)-axis, the magnitude of its \(y\)-coordinate remains the same but its sign changes. But the \(x\)-coordinate remains the same. This is because we are taking it to the quadrant below it. So, we can say that \({\text{R}}_{x}(x,y) = (x,-y)\).
What will be the reflection of the point \((3,-5)\) in the \(x\)-axis?
We have
\[\begin{align}
{\text{R}}_x (x,y) & = (x,-y)\\ {\text{R}}_x (3,-5) & = \big(3,-(-5)\big)\\ & =(3,5).\ _\square \end{align}\]
While reflecting a point about the \(y\)-axis, the magnitude of its \(x\)-coordinate remains the same but its sign changes. But the \(y\)-coordinate remains the same. This is because we are taking it to the quadrant beside it. So, we can say that \({\text{R}}_{y}(x,y) = (-x,y)\).
What will be the reflection of the point \((2,4)\) in the \(y\)-axis?
We have
\[\begin{align}
{\text{R}}_y (x,y) & = (-x,y)\\ {\text{R}}_y (2,4) & = (-2,4).\ _\square \end{align}\]
While reflecting a point in the origin, the magnitude of its coordinates remains the same but their signs change. This is because we are taking it to the diagonally opposite quadrant. So, we can say \({\text{R}}_o (x,y) = (-x,-y)\).
What will be the reflection of the point \((-13,6)\) in the origin?
We have
\[\begin{align}
{\text{R}}_o (x,y) & = (-x,-y)\\ {\text{R}}_o (-13,6) & = \big(-(-13),-6\big)\\ & =(13,-6).\ _\square \end{align}\]
In two dimensions, it is also possible to reflect across any line of the form \(y=mx\) \((\)note that the special case \(x=0\) is the same as reflecting over the \(y\)-axis\(),\) and once this is done we can easily extend to \(mx+b\) by shifting the \(y\)-coordinates by \(b\). It is possible to obtain a general formula for the reflected point \((x',y'):\)
\[(x',y') = \left(2\dfrac{x+(y-b)m}{1+m^2}-x,\ 2\dfrac{x+(y-b)m}{1+m^2}x-y+2b\right).\]
The expression above can be obtained using vectors. Again, let \(y=mx\) or \(\lambda \langle 1, m \rangle\), and let \(\mathbf{p}=\langle x,y \rangle\). If the projection of \(\mathbf{p}\) onto the line is the vector \(\mathbf{l}\), we can easily find \(\mathbf{p'} = 2 \mathbf{l}-\mathbf{p}\). Fortunately, there is a simple formula for the projection of a vector onto another, which gives \((\)here, we can treat the line as a vector by choosing \(\lambda>x\) and taking that point as \(\mathbf{r})\)
\[\displaystyle \mathbf{l}= \frac{ \mathbf{p} \cdot \mathbf{r} }{ \left|\mathbf{r} \right|^2 } \mathbf{r}.\]
This leaves you with a way to calculate \((x',y') = \mathbf{p'} = 2 \frac{ \mathbf{p} \cdot \mathbf{r} }{ \left|\mathbf{r} \right|^2 } \mathbf{r}-\mathbf{p}\) without any trig functions (if you use rotation matrices).
Specifically, you can simplify what we have above to \((x',y') = \left(2\frac{x+ym}{1+m^2}-x,\ 2\frac{x+ym}{1+m^2}x-y\right)\), which is a nice formula that can be applied in many situations. If we want \(mx+b\), we apply \(y \to y-b\) and add \(b\) to \(y'\) \((\)these are the coordinate shifts talked about before the proof: we move everything down by \(b\), apply our formula, then move everything up by \(b)\) to get
\[\displaystyle (x',y') = \left(2\frac{x+(y-b)m}{1+m^2}-x,\ 2\frac{x+(y-b)m}{1+m^2}x-y+2b\right).\ _\square\]
Reflection Symmetry
An interesting application of the reflection across a line is that the graph of a function and its inverse function are symmetric about \( x = y \).
As we know, \(y=f(x) \implies x=f^{-1}(y)\) and this can be interpreted as a change of coordinates \(x\) and \(y\), so we can define the graph of \(f^{-1}(x)\) as the reflection of the graph of \(f(x)\) across the line \(y=x\).
 For the function \(f(x)={x}^5+1\), find the number of real values of \(x\) such that \(f(x)={f}^{-1}(x)\).
For the function \(f(x)={x}^5+1\), find the number of real values of \(x\) such that \(f(x)={f}^{-1}(x)\).
Problem Solving
You are given two fixed points \(A\) and \(B\) on the same side of an arbitrary straight line. Find the minimum perimeter of the triangle formed by the two fixed points and a third point \(C\) which could be anywhere on the line.
Idea to work on: the third point lies on the intersection of the straight line joining the image of one point and the second point with the given line.
About the \(y\)-axis, for which of the following reflection of \(f(x)\) is \(f(x)?\)
Let \(ABC\) be an equilateral triangle with perimeter \(24 \text{ cm}\). Let \(M\) be the midpoint of \(AC\). Let \(L\) and \(N\) be points on \(AB\) and \(BC,\) respectively, such that the perimeter of triangle \(LMN\) is at a minimum.
Find this minimum perimeter.
For some constant \( a> 1 \), the two functions \(f(x) = a^x\) and \(g(x) = \log_a x\) intersect exactly once.
What is \(a?\)