Rocket Physics
Rocket physics plays a crucial role in the modern world. From launching satellites into orbit to testing Intercontinental Ballistic Missiles (ICBMs), principles of rocket mechanics have innumerable applications. The history of rockets goes back to the first century Chinese who used rockets as fireworks to ward off bad spirits, and since then rockets have evolved tremendously. The principles behind rocket propulsion describe a fundamental kind of motion, and to understand it, we need to be familiar with Newton's laws of motion.

Contents
What are rockets?
A rocket is a cylindrical projectile that can be propelled to a great height or distance by the combustion of its contents, used typically as a firework or signal, and used for scientific purposes as an engine to carry payloads including satellites.
The propulsion of a rocket is achieved by ejecting fuel at very high velocities opposite to the desired direction of motion. This propulsion is governed by Newton's third law, which states as follows:
Newton's Third Law
Every action has an equal and opposite reaction. That is, if a particular amount of force is applied on an object in a given direction, the object in return will exert the same amount of force in the opposite direction.
This clip from the cop drama "Brooklyn 99" shows the operation of a fire extinguisher-propelled roller chair cart, which operates by the same principles that govern rocket motion. Extinguisher fluid is ejected out the back at high velocity, which gives the roller chair cart significant momentum in the opposite direction.

Velocity of a Rocket as a Function of Mass
Up to this point, we have come to understand how rockets fly in concept. Let us now derive the central equation for the motion of a thrust-propelled rocket. The calculations that govern rocket motion are somewhat complicated, so let us proceed from the basics.
The motion of a rocket is essentially an effect of the conservation of momentum. That is, for a given isolated system, the total momentum will remain constant. Thus, if the main part of the rocket gains any speed in a given direction, it can only come from ejecting fuel with some velocity in the opposite direction. This movement occurs such that the gain in momentum by the rocket is balanced perfectly by the momentum imparted to the fuel that is ejected.
The simplest way to analyze the motion is to consider a rocket in the moment before, and after, the release of a packet of fuel of mass \(\Delta m\). For simplicity, we consider the frame of an observer who travels with the initial velocity of the rocket.
Prior to combusting the fuel and ejecting it, the whole rocket is cruising along with constant momentum \(M\vec{V}_\text{ship}\).
To boost the rocket velocity, a packet of fuel of mass \(\Delta m\) (boxed in black in the diagram below) is combusted and ejected backward with velocity \(\vec{u}\) relative to the rocket, which reduces the rocket mass by \(\Delta m\), and increases the rocket velocity by an amount \(\Delta \vec{v}_\text{ship}\).
This is the situation illustrated in the diagram below:

Because there is no outside force acting on the system (with the system taken to be the rocket and its fuel), the change in total momentum must be zero. If we subtract the total momentum before the combustion from the total momentum after combustion, we have
\[\begin{align} 0 &= \Delta p \\ &= p_t - p_0 \\ &= \Delta m \left(\vec{V}_\text{ship} - \vec{u}\right) + \left(\vec{V}_\text{ship} + \Delta \vec{v}_\text{ship} \right) \left(M - \Delta m\right) - \vec{V}_\text{ship} M \\ &= \vec{V}_\text{ship} \left(\Delta m - \Delta m\right) - \vec{u}\Delta m + M \Delta \vec{v}_\text{ship} + \vec{V}_\text{ship}\left(M - M\right) \\ &= -\vec{u} \Delta m + M \Delta \vec{v}_\text{ship}, \end{align} \]
which yields the following relationship between the changes in mass and velocity:
\[\vec{u}\Delta m = M \Delta \vec{v}_\text{ship}.\]
Why could we neglect the \(\Delta \vec{v}_\text{ship} \Delta m\) term in the calculation above?
If we rearrange this equation, and take the limit where the \(\Delta\)s become infinitesimal quantities \((\Delta m \rightarrow dm \), and \(\Delta \vec{v}_\text{ship} \rightarrow dv), \) we have
\[\frac{dm}{M} = u^{-1}dv.\]
Finally, we have \(dm = -dM\) (the change in mass of the rocket is equal to minus the mass of the infinitesimal fuel packet), so our relation becomes
\[-\frac{dM}{M} = u^{-1}dv.\]
This says that as our rocket gets lighter and lighter, it needs to eject less and less fuel to get a velocity boost of the same magnitude. Unfortunately, this only works up to a point, when our rocket runs out of fuel entirely and reaches \(v_\text{max}\).
We can integrate this relation from the beginning of fuel combustion to the end, to get the velocity as a function of the current mass of the rocket:
\[ \begin{align} u^{-1}\int_{v_0}^{v_f}dv &= -\int_{M_0}^{M_t} \frac{dM}{M} \\ v_f &= v_0 + u\ln \frac{M_0}{M_t} . \end{align} \]
This shows that the velocity of the rocket ship is a pure function of the mass of fuel that's been ejected up until the current time. It doesn't matter how quickly or slowly the mass was lost, simply the total amount that's been combusted by the current time.
 Velocity of a rocket in space as a function of fuel combusted
Velocity of a rocket in space as a function of fuel combusted
Carry out the calculation for \(v_t\) as a function of \(M_t\) in the case that the rocket is not in free-space, but is fighting a vertical gravitational field of strength \(g\). Is \(v_t\) still a state function of \(M_t,\) or is \(v_t\) now dependent on the history of fuel usage encoded in \(M_t?\)
 Two long barges are moving in the same direction in still water, one with a speed of 10 km/h and the other with a speed of 20 km/h. While they are passing each other, coal is
shoveled from the slower to the faster one at a rate of 1000 kg/min.
Two long barges are moving in the same direction in still water, one with a speed of 10 km/h and the other with a speed of 20 km/h. While they are passing each other, coal is
shoveled from the slower to the faster one at a rate of 1000 kg/min.
How much additional force must be provided by the driving engines of (a) the faster barge and (b) the slower barge if neither is to change speed?
Assume that the shoveling is always perfectly sideways and that the frictional forces between the barges and the water do not depend on the masses of the barges. Choose the answer that equals the sum of answers to (a) and (b).
Problem credit: Fundamentals of Physics Extended, 9th Edition
Escape velocity of a rocket:
This is the minimum velocity required by the rocket to escape the gravitational attraction of the Earth and escape into the space. The kinetic energy of the rocket at a certain height \(h\) is given by the following equation which can help us derive an expression for the escape velocity:
\[\dfrac12mv^2=\dfrac{GMm}R-\dfrac{GMm}{R+h}.\]
From the physics point of view, a rocket on a launchpad is a stored form of energy. It needs to use this energy to attain a velocity greater than the escape velocity of the earth, where the escape velocity can be calculated as follows:
\[\dfrac12mV_e^2=\dfrac{GM_em}{R_e}\implies V_e^2=\dfrac{2GM_e}{R_e}\implies V_e=\sqrt{\dfrac{2GM_e}{R_e}} \approx 11.2km/s.\]
Impulse of a Rocket
Impulse is defined as a force acting on an object over time, which in the absence of opposing forces, changes the momentum of the object. As such, it is the best performance class indicator of a rocket, rather than takeoff thrust, mass, or "power". The total impulse of a rocket burning its propellant is given by:
\[ I = \int F dt.\]
When the thrust is fixed, it is simply: \(I= F t\). The total impulse of a multi-stage rocket is the sum of the impulses of the individual stages.
Parts of a Rocket
Let's now get to know the basic outer features of a rocket. According to NASA, there are four major systems in a rocket:
- structural system
- payload system
- guidance system
- propulsion system.
These four most basic components make up a very complex rocket.

Structural and Payload System of a Rocket
The structural system of a rocket is like an outer skeleton which includes all of the parts which make up the frame of the rocket, i.e. the cylindrical body, the control fins, and the fairings.

The function of the structural system is to minimize the amount of aerodynamic drag created during the flight. The shape of the rocket, hence, plays an important role and so does the structure. But the most important thing to be noted is that the system is to made up of light weight materials which are strong enough to withstand the flight. To solve this problem, alloys of light weight but strong materials such as titanium or aluminium are used.
Recently, the metals have been replaced by the carbon fiber materials, but except for the outer spacecraft bulkhead itself. Bulkheads are still made from titanium, aluminum or other conventional metals and alloys because of the tremendous thermal and pressure demands.
The performance of the rocket depends directly on the weight of the structure. The distribution of the structural weight also affects the center of gravity of the rocket which, in turn, affects the stability and control of the rocket.
Payload system is the most important part of the rocket, which carries the subjected satellite, telescopes, missiles or humans etc. to the required destination safely. Safety is the most important aspect of this system, so it must carry the object without any damages.
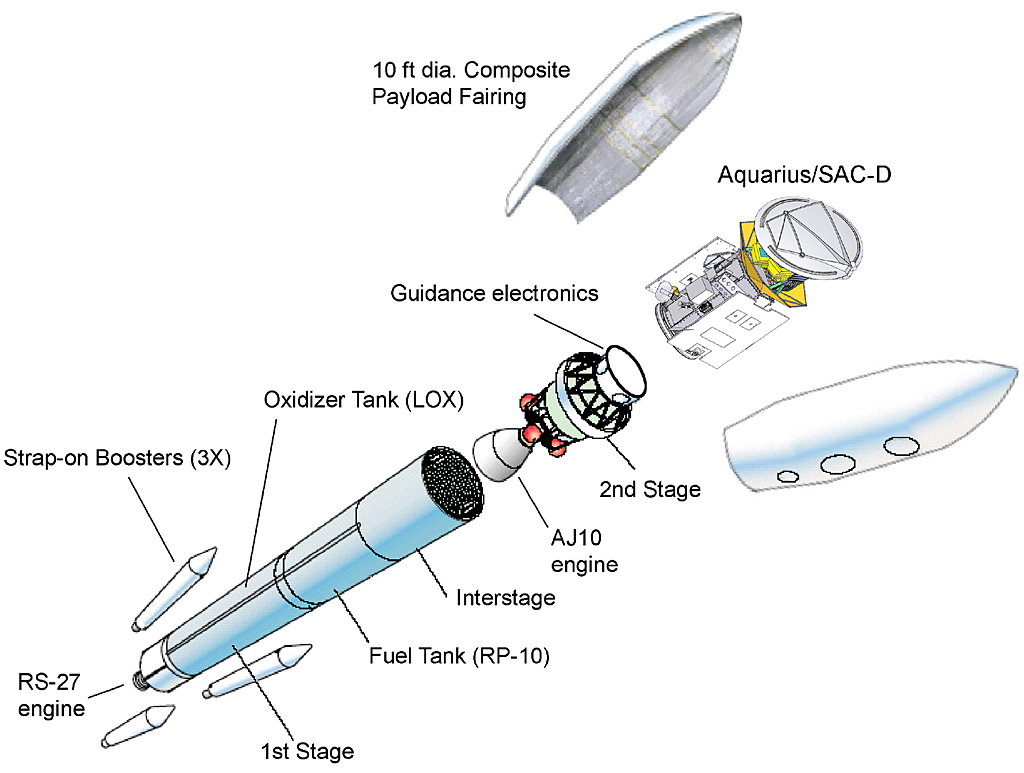
You can see the payload Aquarius/SAC-D, safely kept at the top most part of the rocket.
Payloads of the early period were usually fireworks or crackers for fun making. In the World War II era, most of the payloads in the rockets were missiles equipped with self monitoring systems to destroy cities. Nowadays the payloads are mostly satellites, for various scientific purposes.
Guidance and Propulsion System of a Rocket
The guidance system of a rocket includes very sophisticated sensors, on-board computers, radars, and communication equipment. The guidance system has two main roles during the launch of a rocket: to provide stability for the rocket, and to control the rocket during maneuvers.

One component of the guidance system of a simple rocket is the fins, which act as the steering of the rocket. For complex rockets, the guidance system is computer-based or remote control system. Without the guidance system, a rocket during its flight can be subjected to small gusts of wind or thrust instabilities, which can cause it to "wobble" or change its attitude in flight.
A rocket is said to have a stable guidance system if it naturally returns to its flight configuration when it is disturbed from that configuration. A stable guidance system can correct its mistake on its own without human influence.
The propulsion of a rocket includes all of the parts which make up the rocket engine: the tanks pumps, propellants, power head, boosters, and rocket nozzles, etc. The whole purpose of the propulsion system is to produce thrust.

A rocket engine has a combustion chamber where the oxygen and fuel get mixed up and are exploded. This explosion causes a downward thrust, and as discussed earlier, every action has an equal and opposite reaction. The air around the chamber pushes the rocket upward.
Rocket propulsion in space:

We know that rockets propel on Earth as they exert the thrust on the air. Because of Newton's third law, the air pushes the rocket forward.
Then how does a rocket propel in outer space where there is no air?
Think of an explosion inside a sealed box. The explosion, which is basically no more than a very rapid expansion of a compressed gas, pushes the box apart evenly in all directions. Now imagine that the same explosion takes place in a box that is open at the bottom.
The explosion pushes against the sides of the box evenly, but the force against the top of the box is not balanced by any force against the bottom because the bottom isn't there to push against.
Result: the box flies into the air because of the force of the expanding gas on the top. A rocket engine is essentially that box with a continuous series of explosions going off inside it.
Air actually makes rockets less efficient because of the drag it imparts, especially at the speeds a rocket can travel. \(_\square\)