Semiconductors
Semiconductors are materials whose energy band structure has a small energy gap, allowing for limited conductivity at low temperatures and increased conductivity at higher temperatures. Doped semiconductors, whose properties have been altered with small amounts of impurities, can be used to construct semiconductor junctions with desired electrical properties. Semiconductor devices form the basis of many modern electronic devices, such as integrated circuits and light-emitting diodes.

Band Structure
Fundamentally, the electrical conductivity of materials must be explained quantum mechanically. But this ought not to be too surprising: how else could one account for the fact that elemental materials whose atomic numbers differ only by one or two can have hugely differing properties? Clearly, the answer must lie at the atomic level.
As a simple model, consider a one-dimensional periodic potential \( V \) consisting of delta functions centered at the origin and spaced at a regular interval of \( a \). Each delta function represents a stationary nucleus in a lattice:
\[ V(x) = \alpha \sum_j \delta(x - j a). \]
Furthermore, for simplicity, suppose that after some large number of periods \( N \), the \(x\)-axis "wraps around" so that \( x + Na \) becomes the same thing as \( x \)
One can show that the periodicity of the potential requires that the solution \( \psi \) to the Schrödinger equation must satisfy
\[ \psi(x) = e^{iKa} \psi(x) \]
for some \( K \). Meanwhile, the free particle wavefunction looks like
\[ \psi(x) = A\sin{kx} + B\cos{kx} \]
for \( k = \sqrt{2mE/\hbar} \), where \( E \) is the energy of the system. Solving for \( A \) and \( B \) yields
\[ \cos{Ka} = \cos{ka} + \frac{m\alpha}{\hbar^2 k} \sin{ka}. \]
It turns out that \( Ka = 2\pi n/ N \), where \( n \) is an integer. Since one generally takes \( N \gg n \), \( \cos{Ka} \) can essentially take on any value between \( -1 \) and \( 1 \). Due to the periodicity of both sides of the equation, the corresponding allowed \( k \) and, equivalently, allowed energies \( E \) come in a number of clusters called bands. The bands are separated by gaps.
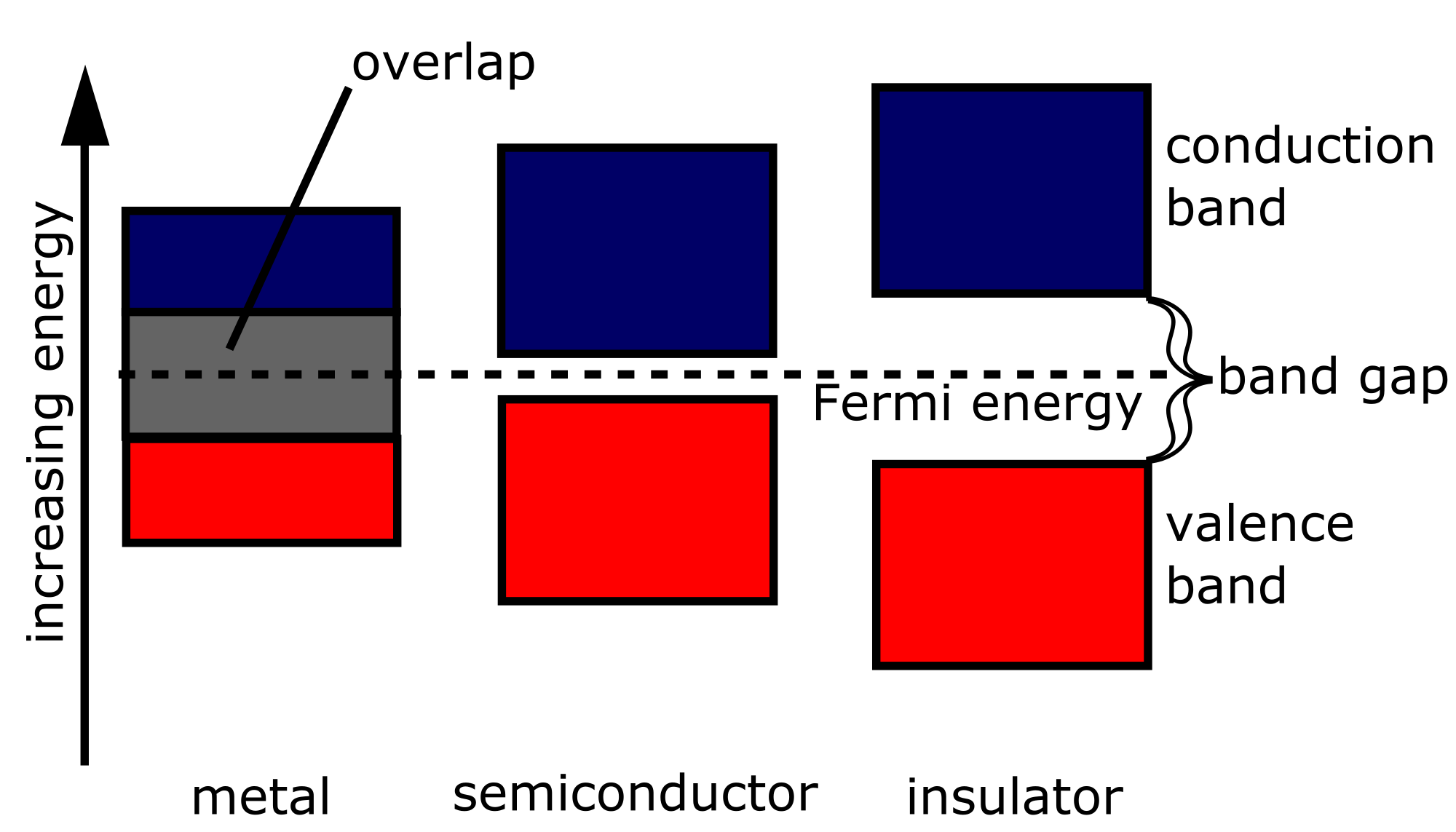
In any given material, any number of bands may be fully or partly occupied by electrons or otherwise empty. Consider the highest-energy fully occupied band, the so-called valence band and the next higher band, the conduction band.
If the conduction band is partly filled, then electrons are relatively easy to excite since there are many closely spaced energy levels within the conduction band that are accessible. Materials with such a band structure tend to be conductors, whose electrons are rather mobile.
If the conduction band is empty, then electrons are difficult to excite. No more electrons can be placed within the valence band, so exciting an electron requires sufficient energy to jump the gap to the conduction band. In an insulator, the energy gap is in excess of available thermal energy, and the electrons remain relatively immobile.
In a semiconductor, the conduction band is empty, but the energy gap is relatively small, on the order of \( 1 \, \text{eV} \) or less. While the thermal energy available at very low temperatures is still not sufficient to jump the gap, at somewhat higher temperatures, it is possible to excite electrons into the conduction band. While the electrons in semiconductors are not typically as mobile as those conductors, semiconductors do display some degree of conductivity.
Suppose that an intrinsic semiconductor has a band gap energy of \( 0.5 \, \text{eV} \) and that the Fermi level (the hypothetical "natural" energy level for an electron in this material) lies at the top of the conduction band. What is the probability that the lowest-energy state of the conduction band is occupied at room temperature (\( 300 \, \text{K} \))?
Use the fact that that electrons are distributed according to the Fermi-Dirac distribution
\[ f(E) = \frac{1}{e^{(E-E_F)/(kT)} + 1}, \]
where \( E_F \) is the energy of the Fermi level, \( T \) is the temperature, and \( k \) is the Boltzmann constant.
Suppose that an intrinsic semiconductor has a band gap energy of \( 0.1 \, \text{eV} \) and that the Fermi level (the hypothetical "natural" energy level for an electron in this material) lies at the top of the conduction band. What is the probability that the lowest-energy state of the conduction band is occupied at room temperature (\( 300 \, \text{K} \))?
Use the fact that that electrons are distributed according to the Fermi-Dirac distribution
\[ f(E) = \frac{1}{e^{(E-E_F)/(kT)} + 1}, \]
where \( E_F \) is the energy of the Fermi level, \( T \) is the temperature, and \( k \) is the Boltzmann constant.
Impurities and Semiconductor Devices
When an electron is excited from the valance band to the conduction band, a hole is left in the valence band. Many elements, such as germanium and silicon, are intrinsic semiconductors and have as many electrons in the conduction band as they do holes in the valence band. Once holes are formed, additional electrons can become mobile by occupying the holes.
However, one can also create semiconductors by the process of doping, or adding specified impurities to other elements. \( n \)-type semiconductors contain impurities with extra valence electrons that lie right below the bottom of the conduction band, making it easy for the impurity atoms (here known as the donor) to donate an electron into the conduction band. \( p \)-type semiconductors contain impurities with a deficit of valence electrons, which lie right above the valence band. The impurity atoms (here known as the acceptor) take an electron from the valence band, thereby creating a hole in the valence band and allowing for further excitation.
Differently-doped semiconductors can be assembled into various types of junctions, which control the flow of electrons in different ways or perform various functions in electronic circuits. For instance, the typical \( p \)-\( n \) junction consists of a layer of \( n \)-type semiconductor on a sample of \( p \)-type material. Under normal operating conditions, current readily flows in the forward bias from \( p \) to \( n \) but not the other way around.
Transistors, which can act as amplifiers and switches, are formed from several \( p \)-\( n \) junctions. A bipolar junction transistor consists of a \( p \)-\( n \)-\( p \) or \( n \)-\( p \)-\( n \) configuration. Another common type is a field-effect transistor, which often consists of \( p \)-type silicon with two \( n \)-type regions etched above, a drain and a source.
Integrated circuits can be made by etching millions of transistors and other components onto small chips the order of a square centimeter or smaller. The modern semiconductor industry is what allows for the production of computing devices on the scale needed to support modern technology.
References
[1] Griffiths, D.J. Introduction to Quantum Mechanics. Second edition. Pearson, 2004.
[2] Young, H.D. University Physics. Thirteenth edition. Pearson, 2012.