Union and Intersection
The union of 2 sets \(A\) and \(B\) is denoted by \( A \cup B \). This is the set of all distinct elements that are in \(A\) or \(B \). A useful way to remember the symbol is \(\cup\)nion. We can define the union of a collection of sets, as the set of all distinct elements that are in any of these sets.
The intersection of 2 sets \(A\) and \(B\) is denoted by \(A \cap B \). This is the set of all distinct elements that are in both \(A\) and \(B\). A useful way to remember the symbol is i\(\cap\)tersection. We define the intersection of a collection of sets, as the set of all distinct elements that are in all of these sets.
If \( A = \{ 1, 3, 5, 7, 9 \} \) and \( B = \{ 2, 3, 5, 7, \} \), what are \( A \cup B \) and \( A \cap B \)?
We have
\[\begin{align} A \cup B &= \{ 1, 2, 3, 5, 7, 9 \} \\ A \cap B &= \{ 3, 5, 7 \}. \ _\square \end{align}\]
A great way of thinking about union and intersection is by using Venn diagrams. These are explained as follows:
We will represent sets with circles.
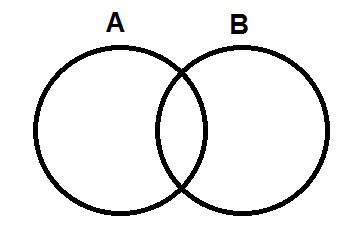
Then we can put the values in appropriate areas.
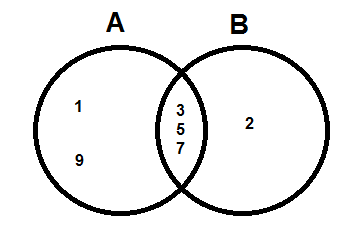
The Union is any region including either A or B.
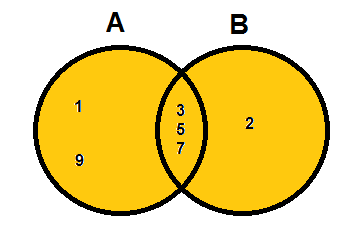
The Intersection is any region including both A and B.

The diagrams we have drawn are called the Venn diagrams.