Sine Rule (Law of Sines)
The law of sines is a relationship linking the sides of a triangle with the sine of their corresponding angles.
Sine Rule
Given the following triangle \( ABC \) with corresponding side lengths \( a, b\) and \( c\):
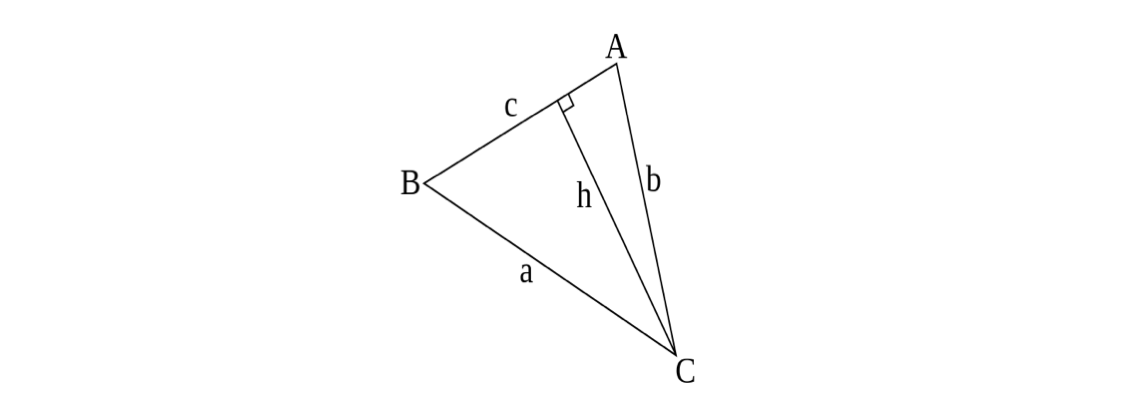
the sine rule or law of sines is the following identity:
\[ \frac { a}{ \sin (A)} = \frac {b}{\sin (B)} = \frac {c} {\sin (C)}. \]
We will prove the first identity
\[ \frac { a}{ \sin (A)} = \frac {b}{\sin (B)}. \]
The second equality can be proved similarly.
By drawing the height \(h\) of the triangle from vertex \(C\) to the opposite side, we can express the height \(h\) in two different ways:
- First, we have \(\sin A = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{b}\), which implies \(h = b\sin(A).\)
- Also, \(\sin B = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{a}\), which implies \(h = a\sin(B).\)
By equating these values of \(h\), we have
\[\begin{align} b \sin(A) &= a \sin(B) \\ \frac{a}{\sin(A)} &= \frac{b}{\sin(B)}. \end{align}\]
By drawing the height \(h\) from the other two vertices, we can similarly show the second equality. \(_\square\)
See the extended sine rule for another proof.
Examples
One real-life application of the sine rule is the sine bar, which is used to measure the angle of a tilt in engineering. Other common examples include measurement of distances in navigation and measurement of the distance between two stars in astronomy.
In the following triangle, suppose that \(a= 1, \angle A = 30^\circ,\) and \(\angle B = 45^\circ\). \[\]
What is the side length \(b?\)
From the sine rule, we have
\[ \begin{align} \frac{a}{\sin(A)} &= \frac{b}{\sin(B)} \\ \frac{1}{\sin(30^\circ)} &= \frac{b}{\sin(45^\circ)} \\ \frac{1}{\ \frac{1}{2}\ } &= \frac{b}{\ \frac{\sqrt{2}}{2}\ } \\ \frac{2 \cdot \sqrt{2}}{2}&= b. \end{align}\]
Therefore, \(b= \sqrt{2}\). \(_\square\)
Ambiguous Case
A common application of the sine rule is to determine the triangle \( ABC\) given some of its sides and angles. The ambiguous case refers to scenarios where there are 2 distinct triangles that satisfy such a configuration. This occurs when we are given the angle-side-side, as shown in the diagram below:

If the side lengths of \(\triangle ABC\) are \(a = 9\) and \(b=10\) with \(\angle A\) opposite to \(a\) measuring \(26\) degrees, what is the measure of \(\angle B\) opposite to \(b?\)
By the sine rule, we have \(\frac a{\sin A} = \frac b{\sin B}\) or \(\frac{9}{\sin 26^\circ} = \frac{10}{\sin B} \). Solving for \(B\) yields \(\sin B = \frac{10}9 \sin 26^\circ\) or \(B \approx 29.149^\circ\).
However, note that \(\sin x = \sin(180^\circ - x) \). Since \(A + B < 180^\circ \) and \(A + (180^\circ - B) < 180^\circ ,\) another possible measure of \(B\) is approximately \(180^\circ - 29.149^\circ =150.851^\circ\). \(_\square\)
Using the same example given above, find the measure of \(\angle B\) if the side lengths were swapped: \(a=10\) and \(b=9\).
By the sine rule, we have \( \frac a{\sin A} = \frac b{\sin B} \) or \( \frac {10}{\sin 26^\circ} = \frac9{\sin B} \). Solving for \(B\) yields \(\sin B = \frac9{10} \sin 26^\circ \) or \(B \approx 23.237^\circ\).
However, note that \(\sin x = \sin(180^\circ - x) \). Since \(A + B < 180^\circ \) but it is not true that \(A + (180^\circ - B) < 180^\circ, \) there is only one possible measure of \(B\), which is approximately \(23.237\) degrees. \(_\square\)
Using the very first example given above, if you are further given the angle of \(B\) to be 13 degrees, what is the total possible number of distinct measures of \(\angle C?\)
By the sine rule we have \( \frac a{\sin A} = \frac b{\sin B} \) or \( \frac {10}{\sin 46^\circ} = \frac9{\sin 13^\circ} \), which is clearly false, implying there is no such triangle. Hence there is no possible triangle that fits these criteria. \(_\square\)
Extended Sine Rule
The extended sine rule is a relationship linking the sides of a triangle with the sine of their corresponding angles and the radius of the circumscribed circle. The statement is as follows:
Given triangle \( ABC \), with corresponding side lengths \( a, b\) and \( c\) and \( R\) as the radius of the circumcircle of triangle \( ABC\), we have the following:
\[ \frac { a}{ \sin A} = \frac {b}{\sin B} = \frac {c} {\sin C} = 2R. \]
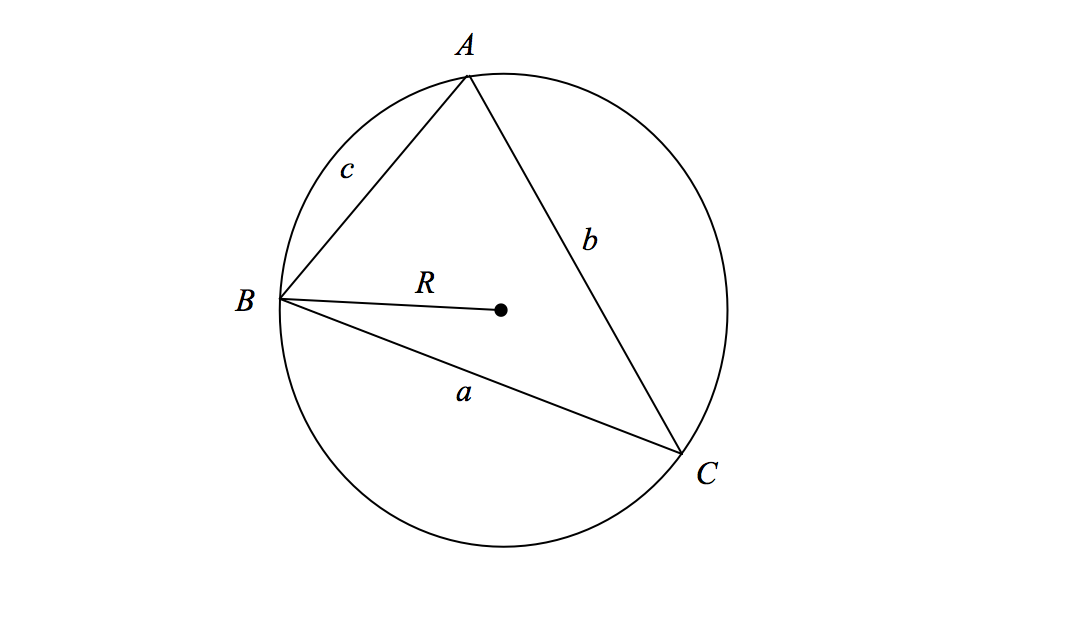
Note: The statement without the third equality is often referred to as the sine rule. The relationship between the sine rule and the radius of the circumcircle of triangle \(ABC\) is what extends this to the extended sine rule.
Extended Sine Rule
Let \( O\) be the center of the circumcircle, and \( D\) the midpoint of \( \overline{BC}.\) Then \(\overline{OD}\) is perpendicular to \(\overline{BC}\). Now, observe that \( \angle BOC\) is equal to \( 2\alpha\) or \( 360^\circ - 2\alpha,\) where \(\angle A=\alpha,\) depending on whether \( O\) is in the triangle or not. Then \( \angle BOD = \alpha\) or \( 180^\circ - \alpha\), and thus \( \sin BOD = \sin \alpha\). As such,
\[ \frac {\ \lvert\overline{BD}\rvert\ }{\lvert\overline{OB}\rvert} = \sin \alpha \implies \frac {a} {\sin \alpha } = 2R.\, _\square \]
Show that the area of triangle \( ABC\) is equal to \( \frac {abc} {4R}. \)
Let \( D\) be the foot of the perpendicular from \( A\) to \( \overline{BC}\). Using \( \overline{BC}\) as the base and \( \overline{AD}\) as the height, the area of the triangle is \( \frac {1}{2} a \cdot \lvert\overline{AD}\rvert\). From right triangle \( CAD\), \( \sin \gamma = \frac {\lvert\overline{AD}\rvert} {b}\). Thus, the area of the triangle is \( \frac {1}{2} a \cdot \lvert\overline{AD}\rvert = \frac {1}{2} a b \sin \gamma\), which is often quoted. Now, using the extended sine rule, we have, \( \frac {c}{\sin \gamma} = 2R\), and thus the area of the triangle is
\[ \frac {1}{2} a b \sin \gamma = \frac {1}{2} a b \frac {c}{2R} = \frac {abc} {4R}. \ _\square \]
