Solving Triangles

To solve problems on this page, you should be familiar with the following:

• Sine Rule
  \[ \frac a{\sin(A) } = \frac b{\sin(B)} = \frac c{\sin(C) } \]
• Cosine Rule
  \[ a^2=b^2+c^2-2bc\cos(A) \\ b^2 = a^2+c^2-2ac\cos(B) \\ c^2= a^2+b^2-2ab\cos(C) \]
• Area of Triangle

\[\text{Area} = \frac12 bc \sin(A)= \frac12 ac \sin(B) = \frac12 ab \sin(C) \]

When we want to solve a triangle, this means that we want to find all/some of the unknown lengths and angles of the triangle.

A triangle \(ABC\) has side lengths \(a = 4\) and \(b= 9,\) and \(C = \cos^{-1} \left(\frac47\right) \). What is the length of the third side, \(c?\)

---

By the cosine rule, we have \(c^2 = a^2 + b^2 - 2ab \cos(C) \). Substituting all the relevant information, we have \(c^2 = \frac{391}7 \). Since \(c\) represents a side length of a triangle, \(c> 0 \) only, so \(c = \sqrt{ \frac{391}7} \approx 7.474\). \(_\square\)

If the area of a triangle is given to be 20 unit squared with two of its side lengths being 7 and 8, what is the sine of the angle in between these two side lengths?

---

Using the area formula, \(\text{Area} = \frac12 bc \sin(A)\implies 20 = \frac12 \cdot 7 \cdot 8 \sin(A). \) Solving for the sine of the angle gives \( \frac57.\ _\square \)

Submit your answer

The diagram to the right shows a triangle \(ABC\) inscribed in a \(6\times 8\) rectangle.

What is the area of this triangle?

---

See Part 2 and Part 3.

The area of an acute triangle is 10, and two side lengths of the triangle are 6 and 7. What is the cosine of the angle in between these two sides?

---

Let the angle between the two sides be \(A.\) Then the area of the triangle is \(10 =\frac12\times 6 \times 7 \times \sin(A), \) which gives \(\sin(A) = \frac{10}{21}.\)

By applying the Pythagorean identity, \( \sin^2(A) + \cos^2(A) = 1,\) so \(\cos(A) = \sqrt{1- \left(\frac{10}{21}\right)^2} = \frac{\sqrt{341}}{21}.\) \(_\square\)

Note that we are only taking the positive root because the cosine of an acute angle is strictly positive.

The numerical value of the area of a triangle is given to be \( \frac{\sqrt[3]{1234}}2 \). What is the relationship between the product of the sides of the triangle to the product of sines of the angles of the triangle?

---

Let \(D\) denote the area of the triangle, then \(\frac{\sqrt[3]{1234}}2 = D = \frac12 ab \sin(C) = \frac12 ac \sin(B) = \frac12 bc \sin(A) \). Then,

\[ D^3 = \frac{1234}8 = \frac18 (abc)^2 \sin(A) \sin(B) \sin(C). \]

So the relationship in question is simply \( \frac{1234}{(abc)^2} = \sin(A) \sin(B) \sin(C).\ _\square\)

Submit your answer

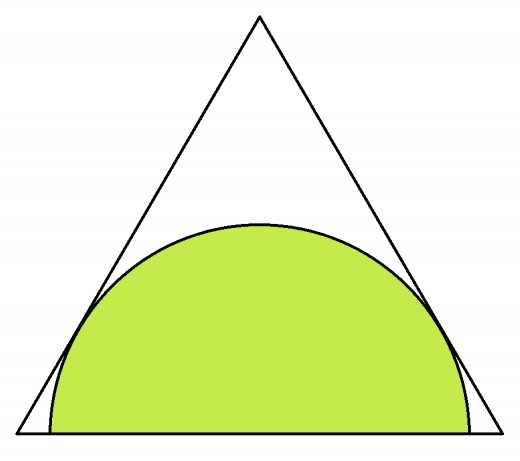
A semi-circle is inscribed within an equilateral triangle such that the diameter of the semi-circle is centered on one side of the triangle and the arc is tangent to the other two sides.

If each side of the triangle is of length 4 cm, then what is the diameter of the semi-circle (in cm)?

Give your answer to 3 decimal places.

Submit your answer

Triangle \(ABC\) has sides of length 24, 35, and 53.

Triangle \(DEF\) has side lengths equal to the lengths of the three medians of triangle \( ABC\).

Find the area of triangle \( DEF.\)

Submit your answer

If \( AP = AC + 2\cdot CB \), what is the measure \(\angle ABP \) in degrees?