Symmetry
Symmetry describes when several parts of an object are identical, such that it's possible to flip, spin, and/or move the object without ultimately changing what it looks like. Symmetry is extremely powerful and beautiful problem-solving tool and it appears all over the place: in art, architecture, nature, and all fields of mathematics! The three basic kinds of 2-dimensional symmetry are reflection, rotation, and translation. After having fun reading through this page, you will be able to recognize all forms of 2-dimensional symmetry.
In fact, soon you won't be able to stop seeing symmetry! It's everywhere, even in the letters on this page for example.
The above are a few letters in the English alphabet that have different styles of symmetry (a rotation and two different reflections).
We will explore all of the beautiful kinds of symmetry in detail below.
Rotations
Rotational symmetry can be seen in some of the most beautiful aspects of nature, art, mathematics, and practical, man-made objects. Here, we will define rotational symmetry, describe the "orders" that rotational symmetry can have, and discuss several interesting examples of rotational symmetry.
Rotational symmetry: An object has rotational symmetry if it looks unchanged after being turned (rotated) by some specific amount less than a full 360-degree spin. The center-point of the spin is called the point of symmetry of the rotation.
Let's look at some of the letters in the alphabet which have rotational symmetry.
Turn any book that you're reading upside-down (a 180-degree rotation)--many letters like S and Z will be 'unaffected.'
Our next step will be to examine the order of rotational symmetry of an object. Let's start with a formal definition of the order of rotational symmetry.
Order of Rotational Symmetry
When an object has rotational symmetry, the order of that symmetry is the number of different positions in which, after some precise amount of rotation, the object looks exactly the same as it did originally.
For example, look at the following diagram:
So the rotational symmetry of an object can have order 2, 3, 4, 5, 6, ..., or any other whole number \(n.\) Except... did we forget to mention the example of rotational symmetry of order 1? No, we did not, and this is intentional. The rotational symmetry of order 1 does not exist since if a shape only matches itself once as we go around (i.e. it matches itself after one full rotation), then there is really no symmetry at all.
What is the order of rotational symmetry of the world's tallest Ferris wheel, also known as the London Eye?
The world's tallest Ferris wheel London Eye has a rotational symmetry of order 32. \(_\square\)
What is the order of rotational symmetry possessed by the parallelogram shown below?
In a parallelogram, the opposite sides are parallel and its diagonals bisect each other.
We will rotate the parallelogram by \(90^\circ\) in each successive turn till one complete revolution and then see how many times it has attained the same look as the original one.
The parallelogram attained the same look two times in one complete rotation, i.e. one after \(180^\circ\) rotation and another after \(360^\circ\) rotation. So the order of rotational symmetry of the parallelogram is also 2. \(_\square\)
Can you find the order of rotational symmetry of the beautiful flower shown below?
It looks the same five times when rotated through a complete cycle. Hence, the order of rotational symmetry of the flower is 5. \(_\square\)
Does the Brilliant logo possess rotational symmetry? If yes, then what is its order?
Let's take the curved triangle as our focal point. Since the triangle is curved unevenly, things will look different from each side. Therefore, the Brilliant logo does not possess rotational symmetry. \(_\square\)
As we have gone through several examples of rotational symmetry, here are some problems based on the same concept:
Reflections
We have gone through several interesting scenarios involving rotational symmetry. To continue our journey, now we will move on to discuss reflection symmetry and the many places where it appears. We will start by defining reflection symmetry.
Reflection symmetry: An object has reflection symmetry if there exists a line that the object can be flipped (reflected) over such that it looks exactly the same before and after the flip. The line that the object flips across is called the axis of symmetry (plural: axes of symmetry).
An object may have 0, 1 or more than one axes of symmetry. An axis of symmetry is also sometimes called a line of symmetry.
For example, the letters A and M, each have a vertical axis of symmetry,
the letters E and K both have horizontal axes of symmetry,
and the letters H and X have both horizontal and vertical axes of symmetry.
How do we know whether any line is an axis of symmetry for an object or not? It is very simple: an axis of symmetry essentially behaves like a mirror. In place of the axis, if we place a mirror, then we should get the same shape. Let's look at an example.
Discuss the symmetry of an Isosceles triangle.
Isosceles Triangles
We see that if we draw a vertical line in the center, then the triangle will be divided into two parts, which are reflections of each other. Therefore an isosceles triangle has reflection symmetry. \(_\square\)
Note: How do we recognize an axis of symmetry in a given object? Well, it's a skill, and it only gets better with practice!
Many geometrical figures have one or more axes of symmetry: squares, rectangles, parabolas, hyperbolas, circles, ellipses, etc. (The list is endless!) But it's easy to be tempted to see extra axes of symmetry. For example, here is a question that most people get wrong if they don't consider it carefully!
Is the diagonal of a rectangle an axis of symmetry?
A common misconception is that all lines that divide a figure into two congruent parts are lines of symmetry. This is not always the case! For example, the diagonal of a (non-square) rectangle is not a line of symmetry. \(_\square\)
Note: If you actually reflect the lower-left half of a rectangle over the diagonal, the figure you form is called a kite.
\(\quad \quad\)
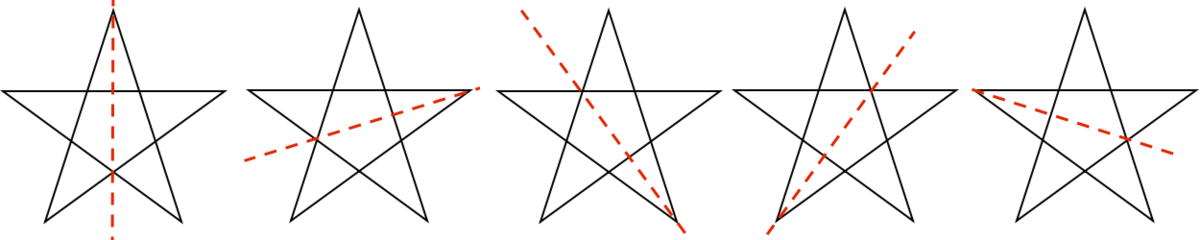
How many lines of symmetry does this regular 5-pointed star have?
The 5-pointed regular star has 5 lines of symmetry. We can see them clearly in the following figure. There is a line of symmetry passing through each of the 5 points of the star. \(_\square\)
The amazing fact that reflection symmetry is abundant in nature as well compels us to love symmetry and we can have fun with it. Here is an interesting fact: More than 99% of the world's animals have reflection symmetry, including the familiar homo sapien species!
Show that the human body possesses reflection symmetry.
From the outside, at first sight the human body at a frontward facing angle appears to be symmetrical. We can draw a vertical axis of symmetry in the center. \(_\square\)
The image of an orchid flower you see above also has reflection symmetry.
Many man-made structures also exhibit reflection symmetry. Symmetry looks beautiful and appeals the eye. It's no wonder so many famous structures are symmetrical. Let's take a tour around the world here through the following examples:
One of the seven wonders of the world: Taj Mahal
The beautiful Adelaide Studios
Here are a few problems for you to try yourself, which will check your understanding of the axes of symmetry.
We can now easily figure out the symmetries present in an object or figure. Let's work out an example and a problem to grab our understanding about the number of lines of symmetry.
How many lines of symmetry does the Mercedes-Benz logo have?
Try counting the number of lines of symmetry without looking at the circle. If the circle wasn't there, and we just had three lines extending from one point, we can easily figure out that there are \(3\) lines of symmetry. \(_\square\)
Consider a regular \(n\)-gon, where \(n\) is an even integer. How many lines of symmetry will this shape have?
There will be several different lines to count:
There are already \(\frac{n}{2}\) lines of symmetry, each one passing through one side and leaving from the opposite. So as not to double count, we divide the number of sides by \(2\).
We will also have another \(\frac{n}{2}\) lines, each one going through one of the \(n\)-gon's corners and leaving from the opposite.
Thus, an \(n\)-gon with an even \(n\) has \(n\) lines of reflective symmetry. \(_\square\)
The amazing fact is that the snowflakes too possess symmetries. Let's get more familiar with the snowflakes through examples and problems.
Discuss the symmetry of the snowflakes.
All snowflakes have rotational symmetry of order 6. Snowflakes are symmetrical because they reflect the internal order of the water molecules as they arrange themselves in the solid state (the process of crystallization). Water molecules in the solid state, such as in ice and snow, form weak bonds (called hydrogen bonds) to one another. These ordered arrangements result in the basic symmetrical, hexagonal shape of the snowflake. \(_\square\)
When he was 20, Wilson Alwyn “Snowflake” Bentley photographed his first snowflake by perfecting the process of catching the flakes on black velvet before they melted or sublimated. He pioneered the art of snowflake photography, and captured over 5000 beautiful images for us.
In the above image, how many lines of symmetry does the snowflake have?
Translations
Wow! Through the sections above, we found that we are surrounded by symmetrical objects, even many living ones! We still have one further kind of symmetry to discuss: translational symmetry. Let's start with the definition of translational symmetry and then we will move on to visualizing the symmetry and playing around with it.
Translational symmetry: Translational symmetry is when a pattern looks the same before and after it has been moved ("translated") a particular distance in a specified direction. Patterns with translational symmetries look like they were created by someone with a stamp, moving in a straight line across a surface and stamping at regular intervals as they move. An example is as follows:
\(\large \color{green}{\text{This wiki page is really awesome!}}\)
\(\large \quad \quad \quad \color{green}{\text{This wiki page is really awesome!}}\)
\(\large \quad \quad \quad \quad \quad \quad \color{green}{\text{This wiki page is really awesome!}}\)
An object or pattern has translational symmetry if it can be slid in some direction and be ultimately unchanged at the end of the motion. For example, an infinitely ongoing series of ellipses (.........) has translational symmetry.
Let's work out some interesting examples with translational symmetry and have fun exploring them.
The graph of \(\text{CO}_2\) in ppm (parts per million) has translational symmetry as you can see in the above graph. The reason behind it is as follows:
Carbon dioxide \((\text{CO}_2)\) is an important heat-trapping (greenhouse) gas, which is released through human activities such as deforestation and burning fossil fuels, as well as natural processes such as respiration and volcanic eruptions.
The seasonal cycle is due to the vast land mass of the Northern Hemisphere, which contains the majority of land-based vegetation. The result is a decrease in atmospheric carbon dioxide during northern spring and summer when plants are absorbing \(\text{CO}_2\) as part of photosynthesis. The pattern reverses, with an increase in atmospheric carbon dioxide during northern fall and winter. The yearly spikes during the cold months occur as annual vegetation dies and leaves fall and decompose, which releases their carbon back into the air.
There are several man-made objects which possess translational symmetry. Here we are listing a few of them, but you are free to explore the objects possessing translational symmetry and have fun with them.
Street Lamps
Train Tracks
Designing Wallpaper
Here's one special case of transnational symmetry: a combination of sorts between a translation and a reflection called a glide reflection.
Glide reflection: A glide reflection is a combination of two transformations: a reflection over a line followed by a translation in the same direction as the line.
Only an infinite strip can have translation symmetry or glide reflection symmetry. For translation symmetry, you can slide the whole strip some distance, and the pattern will land back on itself. For glide reflection symmetry, you can reflect the pattern over some line, then slide in the direction of that line, and it looks unchanged. And the patterns must go on forever in both directions.
For an example, see the following:
Main article: Frieze Patterns
Combining Symmetries
We have gone through all the symmetry types one by one, and now let's apply different types of symmetry in the same problem!
Let's start by working through some interesting examples which use both reflectional and rotational symmetries, but no translational symmetry.
M. C. Escher
We will end this page by mentioning one amazing artist who spent much of his life exploring symmetries and creating stunning designs that combine an advanced understanding of the mathematics involved with awe-inspiring creativity!
M. C. Escher was a Dutch mathematician who dedicated most of his life to studying the mathematics of tessellations. He created drawings which demonstrate the beauty of mathematics through geometry and patterns.
Aperiodic Penrose Tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles, named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose tiling implies no translational symmetry, i.e. a shifted copy of one will never match the original. A Penrose tiling may be made with both reflection symmetry and rotational symmetry of order 5, as in the example below.
Discuss the different symmetries in a circle.
Reflection symmetry: There is an infinite number of lines of reflection symmetry in a circle.
Rotational symmetry: There are also an infinite number of orders of rotational symmetry since you can turn a circle any amount and it will remain unchanged. \(_\square\)
Just one more problem and we will be accomplishing all our objectives of going through this page. Here we go:
A person paints 3 small triangles in the top half of the figure \(\color{blue}{\text{blue}}\). He then paints 5 triangles in each half \(\color{green}{\text{green}}\), leaving 8 in each half remain \(\color{darkorange}{\text{orange}}\). When the upper half is folded down over the center line, 2 pairs of \(\color{blue}{\text{blue}}\) triangles coincide as do 3 pairs of \(\color{green}{\text{green}}\) triangles. There are also 2 \(\color{blue}{\text{blue}}\)-\(\color{darkorange}{\text{orange}}\) pairs.
How many \(\color{darkorange}{\text{orange}}\) pairs coincide?
There are total 16 small triangles in each half and each half has 3 \(\color{blue}{\text{blue}}\) triangles, 5 \(\color{green}{\text{green}}\) triangles, and 8 \(\color{darkorange}{\text{orange}}\) triangles. There are also 2 pairs of \(\color{blue}{\text{blue}}\) triangles, so 2 \(\color{blue}{\text{blue}}\) triangles on each side are used, leaving 1 \(\color{blue}{\text{blue}}\) triangle, 5 \(\color{green}{\text{green}}\) triangles, and 8 \(\color{darkorange}{\text{orange}}\) triangles remaining on each half. Also, there are 3 pairs of \(\color{green}{\text{green}}\) triangles, using 3 \(\color{green}{\text{green}}\) triangles on each side, so there is 1 \(\color{blue}{\text{blue}}\) triangle, 2 \(\color{green}{\text{green}}\) triangles, and 8 \(\color{darkorange}{\text{orange}}\) triangles remaining on each half. Also, we have 2 \(\color{blue}{\text{blue}}\)-\(\color{darkorange}{\text{orange}}\) pairs. This obviously can't use 2 \(\color{blue}{\text{blue}}\) triangles on one side, since there is only 1 on each side, so we must use 1 \(\color{blue}{\text{blue}}\) triangle and 1 \(\color{darkorange}{\text{orange}}\) triangle per side, leaving 2 \(\color{green}{\text{green}}\) triangles and 7 \(\color{darkorange}{\text{orange}}\) triangles apiece. The remaining \(\color{green}{\text{green}}\) triangles cannot be matched with other \(\color{green}{\text{green}}\) triangles since that would mean there were more than 3 \(\color{green}{\text{green}}\) pairs, so the remaining \(\color{green}{\text{green}}\) triangles must be paired with \(\color{darkorange}{\text{orange}}\) triangles, yielding 4 \(\color{green}{\text{green}}\)-\(\color{darkorange}{\text{orange}}\) pairs, one for each of the remaining \(\color{green}{\text{green}}\) triangles. This uses 2 \(\color{green}{\text{green}}\) triangles and 2 \(\color{darkorange}{\text{orange}}\) triangles on each side, leaving 5 \(\color{darkorange}{\text{orange}}\) triangles apiece, which must be paired with each other, so there are 5 \(\color{darkorange}{\text{orange}}\)-\(\color{darkorange}{\text{orange}}\) pairs. \(_\square\)
Let's accomplish the objectives of this page by solving the following problem:
