Tangent and Cotangent Graphs
Contents
Tangent and Cotangent Graphs
From the definition of the tangent and cotangent functions, we have
\[ \tan( \theta)= \frac{\sin(\theta)}{\cos(\theta)},\quad \cot( \theta)= \frac{\cos(\theta)}{\sin(\theta)}.\]
Thus, \(\tan(\theta)\) is not defined for values of \(\theta\) such that \(\cos(\theta) = 0\). Now, consider the graph of \(\cos (\theta)\):
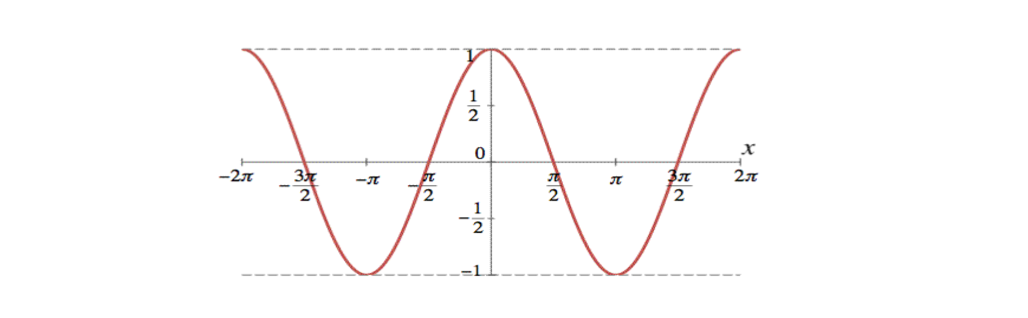
From this graph, we see that \(\cos(\theta) = 0\) when \(\theta = \frac{\pi}{2} + k\pi\) for any integer \(k\). This implies that the tangent function has vertical asymptotes at these values of \(\theta\).
Does the tangent function approach positive or negative infinity at these asymptotes? As \(\theta\) approaches \(\frac{\pi}{2}\) from below \(\big(\theta\) takes values less than \(\frac{\pi}{2}\) while getting closer and closer to \(\frac{\pi}{2}\big),\) \(\sin (\theta) \) takes positive values that are closer and closer to \(1\), while \(\cos (\theta)\) takes positive values that are closer and closer to \(0\). This shows \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\) is positive and approaches infinity, so \(\tan(\theta)\) has a positive vertical asymptote as \(\theta \rightarrow \frac{\pi}{2} \) from below. By a similar analysis, as \(\theta\) approaches \(\frac{\pi}{2}\) from above \(\big(\theta\) takes values larger than \(\frac{\pi}{2}\) while getting closer and closer to \(\frac{\pi}{2}\big),\) \(\sin (\theta) \) takes positive values that are closer and closer to \(1\), while \(\cos (\theta)\) takes negative values that are closer and closer to \(0\). This shows \(\tan(\theta)\) has a negative vertical asymptote as \(\theta \rightarrow \frac{\pi}{2} \) from above. The following shows the graph of tangent for the domain \(0 \leq \theta \leq 2\pi\):
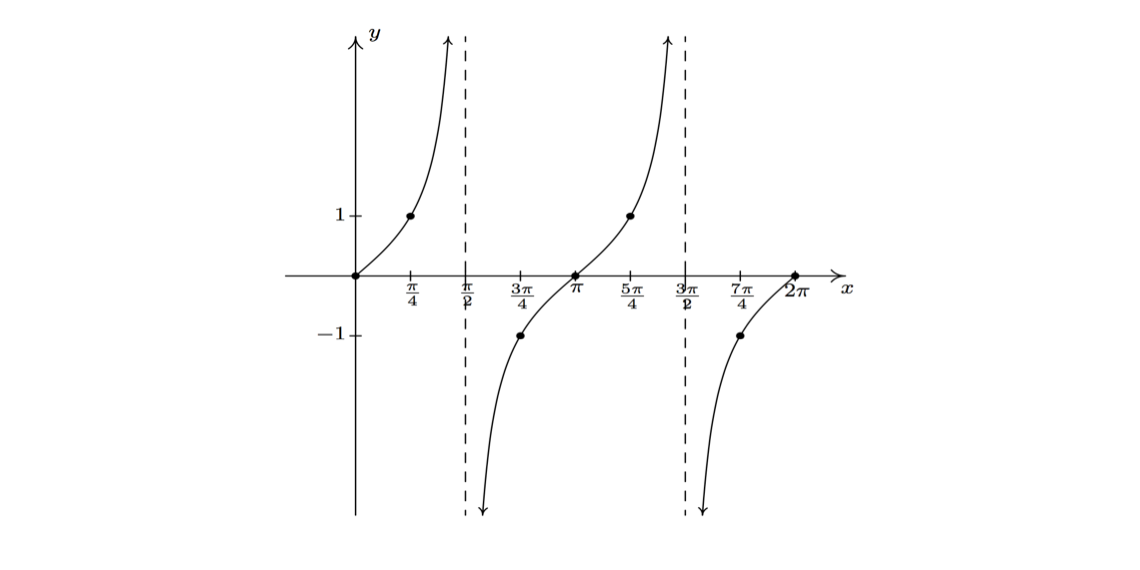
The graph of tangent over its entire domain is as follows:

Similarly, \(\cot(\theta)\) is not defined for values of \(\theta\) such that \(\sin(\theta) = 0\). From the graph of \(\sin (\theta),\) we see that \(\sin(\theta) = 0\) when \(\theta = 0 + k\pi\) for any integer \(k\), which implies that the cotangent function has vertical asymptotes at these values of \(\theta:\)

Relationship between Tangent and Cotangent
Observe that from the definition of tangent and cotangent, we obtain the following relationship between the tangent and cotangent functions:
\[ \tan(\theta) = \frac{\sin (\theta)}{\cos (\theta)} = \frac{1} {\ \ \frac{\cos (\theta)}{\sin (\theta)}\ \ } = \frac{1}{\cot(\theta)}.\]
Indeed, we can see that in the graphs of tangent and cotangent, the tangent function has vertical asymptotes where the cotangent function has value 0 and the cotangent function has vertical asymptotes where the tangent function has value 0.
Properties
The tangent and cotangent graphs satisfy the following properties:
- range: \((-\infty, \infty)\)
- period: \(\pi\)
- both are odd functions.
From the graphs of the tangent and cotangent functions, we see that the period of tangent and cotangent are both \(\pi\). In trigonometric identities, we will see how to prove the periodicity of these functions using trigonometric identities.
Examples
What values of \(\theta\) in the interval \([0, \pi]\) satisfy \(\tan(\theta) = \cot(\theta)?\) Can we see this from the graphs of the tangent and cotangent functions?
We would like to find values of \(\theta\) such that \(\tan(\theta) = \cot(\theta) = \frac{1}{\tan(\theta)}\), i.e. \( \big( \tan (\theta) \big)^2 = 1\). This is satisfied for \(\tan \theta = \pm 1\), or \(\theta = \frac{\pi}{4}, \frac{3\pi}{4}\).
We can also see from the graphs of tangent and cotangent that the points of intersection of the two graphs in the domain \([0,\pi]\) are \( \big( \frac{\pi}{4}, 1 \big)\) and \( \big( \frac{3\pi}{4}, -1 \big).\ _\square \)
