Taylor Series Manipulation

Main article: Taylor Series

A Taylor series is a polynomial of infinite degrees that can be used to represent all sorts of functions, particularly functions that aren't polynomials. It can be assembled in many creative ways to help us solve problems through the normal operations of function addition, multiplication, and composition. We can also use rules of differentiation and integration to develop new and interesting series.

Adding and subtracting power series are as easy as adding the functions they represent! While adding two power series won't always demonstrate a discernible pattern in their coefficients, writing out the first several terms of a sum or difference of power series takes little work.

\[\begin{align} \text{Sum of series: } \sum_{n=0}^{\infty}a_nx^n + \sum_{n=0}^{\infty}b_nx^n &= \sum_{n=0}^{\infty}(a_n + b_n)x^n \\ \text{Product of series: }\left(\sum_{n=0}^{\infty}a_nx^n\right)\left(\sum_{k=0}^{\infty}b_kx^k\right) &= \sum_{n=0}^{\infty}\sum_{k=0}^{n}(a_kb_{n - k})x^n. \end{align} \]

What does the power series for \(f(x) = e^x + \cos x\) look like?

---

We know that \(e^x = \displaystyle\sum_{n = 0}^{\infty} \frac{x^n}{n!}\) and \(\cos x = \displaystyle\sum_{n = 0}^{\infty} (-1)^n \frac{x^{2n}}{(2n)!}\), so their sum would simply be

\[e^x + \cos x = \displaystyle\sum_{n = 0}^{\infty} \left(\frac{x^n}{n!} + \frac{(-1)^nx^{2n}}{(2n)!}\right) \hspace{.1cm} \text{ or } \hspace{.2cm} \displaystyle\sum_{n = 0}^{\infty} x^n \left(\frac{1}{n!} + \frac{(-1)^nx^{n}}{(2n)!}\right).\]

This expression isn't exactly practical to work with, so we'll just find the first few terms of the summation instead.

\[ \begin{align*} e^x + \cos x &= \left(1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \frac{x^6}{6!} + \cdots \right) + \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \right) \\ &= 2 + x + \frac{x^3}{3!} + \frac{2x^4}{4!} + \frac{x^5}{5!} + \cdots. \ _\square \end{align*}\]

We see that adding the power series of two functions is as easy as adding the coefficients of their corresponding powers to create a new power series.

However, we shall see in the next example that multiplication of two power series will take a little more effort...

What does the power series for \(f(x) = e^x\cos x\) look like?

---

The product of the two power series will require some close inspection into term by term multiplication. It's not as simple as just multiplying the coefficients of each \(x^n\)!

\[e^x\cos x = \left(\displaystyle\sum_{n = 0}^{\infty} \frac{x^n}{n!}\right)\left(\displaystyle\sum_{n = 0}^{\infty}\frac{(-1)^nx^{2n}}{(2n)!}\right).\]

It will be easier to list out the first several terms of each series and collect terms based in their power.

\[ \large\begin{align*} e^x\cos x &= \left(1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \right)\left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \right). \end{align*}\]

We'll perform the multiplication in ascending order on the power of \(x\), starting by distributing and collecting the constant, then proceeding on to the coefficient of \(x\), then \(x^2\), and so on.

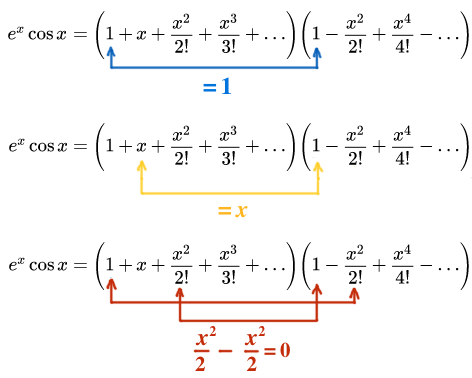
Based on the multiplication done above, we can see that power series expansion begins as follows:

\[\large e^x\cos x = \color{blue}{1} + \color{orange}{x} + \color{red}{0x^2}.\]

What would the next term be if we wanted to collect all terms containing \(x^3?\)

How could we construct the Taylor series for a composition of functions, such as \(e^{x^3}\)? We could attempt to use the method prescribed by the definition of the Taylor series, but we'd soon find that the derivatives required to produce its coefficients become unwieldy, laced with excessive uses of the product and chain rules.

Instead, we can put the Taylor series already known for \(e^x\) to good use. Simply replacing every instance of \(x\) with \(x^3\) in the \(e^x\) Taylor series will create the Taylor series for \(e^{x^3}\).

We have

\[e^x = \sum_{n = 0}^{\infty}\frac{x^n}{n!} \hspace{.2cm} \Longrightarrow \hspace{.2cm} e^{x^3} = \sum_{n = 0}^{\infty}\frac{(x^3)^n}{n!} = \sum_{n = 0}^{\infty}\frac{x^{3n}}{n!}. \]

Moreover, constants and additional powers of \(x\) can be multiplied or divided through a given power series without breaking the summation. For instance, if we wished to create the power series for \(4x^2e^{x^3}\), we need only multiply through the series we constructed by a factor of \(4x^2\).

\[4x^2e^{x^3} = 4x^2\sum_{n = 0}^{\infty}\frac{x^{3n}}{n!} = \sum_{n = 0}^{\infty}\frac{4x^{3n + 2}}{n!}.\]

One of the fascinating results of Taylor series is that the processes of differentiation and integrations hold up rather well.

\[\frac{d}{dx} \sin x = \frac{d}{dx} \sum_{n = 0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!} = \sum_{n = 0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n)!} = \cos x. \]

In the derivative of sine above, we apply the power rule to the term \(x^{2n + 1}\) in sine's power series. Doing so produces a profound result: The resulting summation is the Taylor series for cosine! When it comes to handling derivatives, we find Taylor series are very well-behaved and we use this fact to tackle some interesting problems.

Let's see how the manipulation of the series \(\displaystyle \frac{1}{1 - x} = \sum_{n = 0}^{\infty}x^n\) can help us determine the series for \(\dfrac{x}{(1 - x)^2}\).

\[\begin{align} \frac{d}{dx}\left(\frac{1}{1 - x}\right) &= \frac{d}{dx}\sum_{n = 0}^{\infty}x^n\\ \frac{1}{(1 - x)^2} &= \sum_{n = 0}^{\infty} nx^{n-1}. \end{align}\]

With one swift use of the power rule, we were able to generate a Taylor series for \(\dfrac{1}{(1 - x)^2}\). Pretty amazing! However, we want the power series for \(\dfrac{x}{(1 - x)^2}\), so we can multiply the power series above by an additional factor of \(x\) to achieve the desired result.

\[\frac{x}{(1 - x)^2} = x \cdot \frac{1}{(1 - x)^2} = x \cdot \left(\sum_{n = 0}^{\infty} nx^{n-1}\right) = \sum_{n = 0}^{\infty} nx^{n} .\]

It is worth noting that first term of the summation resulting from the derivative is 0. This should groove with our understanding of the infinite geometric sum \(1 + x + x^2 + \cdots\) as we see that the derivative of the first term is 0. Because the first term in the derivative of the summation is 0, we have no need for it in the summation.

\[\frac{x}{(1 - x)^2} = \sum_{n = 0}^{\infty} nx^{n} = \sum_{n = 1}^{\infty} nx^{n}. \]

This result is the formula for the famous Arithmetic-Geometric Progression.

With slight variations on the theme of differentiating Taylor series, we'll find that integrating Taylor series are just as useful and can help us uncover the series expansions for many other functions. The Taylor series we know and love for \(\displaystyle \tan^{-1} x = \sum_{n=0}^{\infty}(-1)^n \frac{x^{2n + 1}}{2n + 1} \) can be generated by integrating the power series representation of \(\dfrac{1}{1 + x^2}\).

We know that the derivative of \(\tan^{-1} x\) is \(\dfrac{1}{1 + x^2}\). By the geometric power series, we know that

\[\frac{1}{1 + x^2} = \sum_{n = 0}^{\infty} (-1)^nx^{2n}.\]

We need only integrate this series to recover the \(\tan^{-1} x\) we started with.

\[\begin{align} \int\frac{dx}{1 + x^2} &= \int\sum_{n = 0}^{\infty} (-1)^nx^{2n}dx \\ \tan^{-1} x &= \sum_{n = 0}^{\infty} (-1)^n \frac{x^{2n+1}}{2n + 1} + C. \end{align}\]

The constant of integration, \(C\), is necessary as it always is when taking an antiderivative. The initial condition of \(\tan^{-1} 0 = 0\) will be appropriate for helping us determine the value of \(C\).

\[\tan^{-1} 0 = \sum_{n = 0}^{\infty} (-1)^n \frac{0^{2n+1}}{2n + 1} + C = C.\]

Prove that

\[\displaystyle \dfrac1{2! - 1!} - \dfrac1{4! - 3!} + \dfrac1{6!- 5!} - \dfrac1{8! - 7!} + \cdots = \int_0^1 \dfrac{\sin x}x \, dx. \]

---

Since \((n+1)!- n! = n \cdot n! \), the left hand side of the equation can be rewritten as \( \sin x = \displaystyle \sum_{k=1}^\infty \dfrac{ (-1)^{k+1} }{(2k-1) \cdot (2k-1)!} \). Because this series somewhat resembles the Taylor series of \(\sin x\) centered at \(x=0 \), i.e. \( \displaystyle \sum_{k=1}^\infty \dfrac{ (-1)^{k+1} }{ (2k-1)! } \), it is instinctive to think that this series resembles the function \(\sin x\).

But how are they related exactly? Well, the well-known series of \( \sin x\) is \( \displaystyle \sum_{k=1}^\infty \dfrac{ (-1)^{k+1} }{ (2k-1)! } \), whereas our series is \( \displaystyle \sum_{k=1}^\infty \dfrac{ (-1)^{k+1} }{ {\color{red}{(2k-1)}} \cdot (2k-1)! } \). So maybe there's an integration step involved here?

It is actually much easier to see how they are related if we rewrite \(\sin x\) as

\[ \sin x = x -\dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \cdots . \]

Dividing by \(x\) gives

\[ \dfrac {\sin x} x = 1 - \dfrac{x^2}{3!} + \dfrac{x^4}{5!} - \dfrac{x^6}{7!} + \cdots . \]

If we integrate this expression from 0 to 1, the result will follow:

\[\begin{align} \int_0^1 \dfrac{\sin x}x \, dx &= \left [1 - \dfrac{x^2}{3!} + \dfrac{x^4}{5!} - \dfrac{x^6}{7!} + \cdots \right ] _0^1 \\ &= 1 - \dfrac1{3\cdot3!} + \dfrac1{5\cdot5!} - \dfrac1{7\cdot 7!} + \cdots \\ &= \dfrac1{2! - 1!} - \dfrac1{4! - 3!} + \dfrac1{6!- 5!} - \dfrac1{8! - 7!} + \cdots.\ _\square \end{align} \]