Transformation of Resistances (Star to Delta and Delta to Star)

Transformation of resistances is a key tool in solving many problems related to equivalent resistance around a given circuit, etc. It reduces the math work and acts as a bonus while problem solving in competitive exams.

In this section we will understand what are star and delta formations of resistances and also try to identify them in simple circuits.

Star and delta formations of resistances is a standard 3-phase circuit or network of resistances connected in the same way as their name suggests.

Star formation of resistances looks like this:

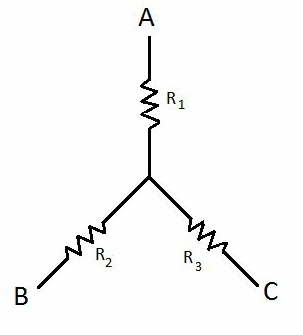
Delta formation of resistances looks like this:

The key to solving problems is to identify them in a simple circuit.

In this section we will convert Delta formation of resistances to Star formation resistances.

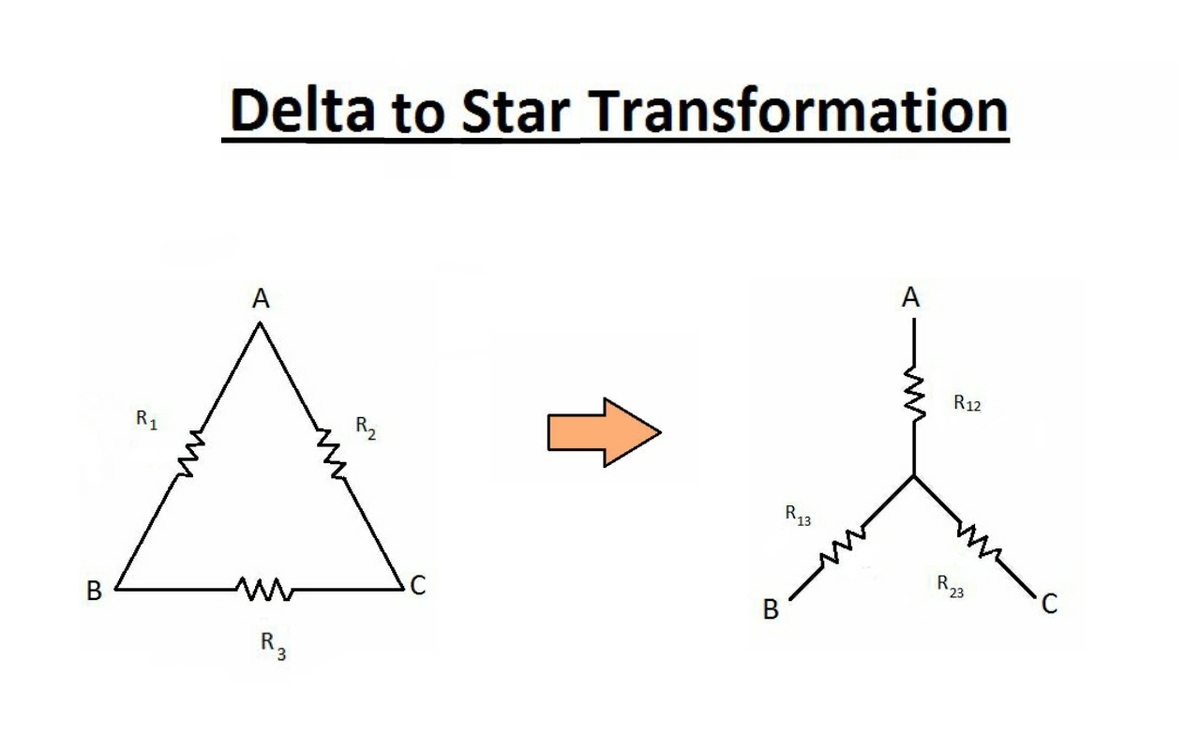
Here is the formula for transformation-

$R_{12} = \frac{R_1.R_2}{R_1+R_2+R_3}$

Note that the above formula is cyclic in nature hence it works the same for $R_{23}$ and $R_{31}$.

Show that $R_{12} = \frac{R_1.R_2}{R_1+R_2+R_3}$

---

Lets consider the resistance from $A$ to $C$:

• $R_{AC,left} = R_2$ in parallel with $R_1 + R_3$
• $R_{AC,left} = \frac{R_2 (R_1+R_3)}{R_2+R_1+R_3}$
• $R_{AC,right} = R_{12} + R_{23}$

Equating the two:

• $\frac{R_2 (R_1+R_3)}{R_2+R_1+R_3} = R_{12} + R_{23}$

Similarly:

• $\frac{R_3 (R_2+R_1)}{R_3+R_2+R_1} = R_{23} + R_{31}$
• $\frac{R_1 (R_3+R_2)}{R_1+R_3+R_2} = R_{31} + R_{12}$

Adding the first two equations, and subtracting the middle equation gives:

$(R_{31} + R_{12}) + (R_{12} + R_{23}) - (R_{23} + R_{31}) = \frac{R_1 (R_3+R_2)}{R_1+R_3+R_2} + \frac{R_2 (R_1+R_3)}{R_2+R_1+R_3} - \frac{R_3 (R_2+R_1)}{R_3+R_2+R_1}$

$2R_{12} = \frac{2R_1R_2}{R_1+R_2+R_3}$

$R_{12} = \frac{R_1R_2}{R_1+R_2+R_3}$

QED

In this section we will convert Star formation of resistances to Delta formation resistances.

We will do this by finding equivalent resitances in place of resistances given in the problem.

For example,

In order to replace $R_1$ and $R_2$ (See Star formation) in the given diagram we will be there equivalent, that is $R_{12}$ (See Delta formation).

Here is the formula for transformation-

$R_{12}=R_1 + R_2 + \frac{R_1.R_2}{R_3}$

Note that the above formula is cyclic in nature hence it works the same for $R_{23}$ and $R_{31}$.

Prove that $R_{12}=R_1 + R_2 + \frac{R_1.R_2}{R_3}$

---

This is the same setup as in the previous setup, with the resistors renamed as follows:

• $R_1 \rightarrow R_{23}$
• $R_2 \rightarrow R_{13}$
• $R_3 \rightarrow R_{12}$
• $R_{23} \rightarrow R_1$
• $R_{13} \rightarrow R_2$
• $R_{12} \rightarrow R_3$

So, the general results of the above proof become:

$R_{3} = \frac{R_{23}R_{13}}{R_1+R_{13}+R_{12}}$

And similarly:

$R_{1} = \frac{R_{13}R_{12}}{R_1+R_{12}+R_{23}}$ $R_{2} = \frac{R_{12}R_{23}}{R_1+R_{23}+R_{13}}$

So,

$R_1 + R_2 + \frac{R_1R_2}{R_{12}} = \frac{R_{12}(R_{23}+R_{13})}{R_{23}+R_{13}+R_{12}} + \frac{R_{13}R_{12}R_{23}R_{12}}{R_{23}R_{13}}$

$R_1 + R_2 + \frac{R_1R_2}{R_{12}} = \frac{R_{12}(R_{23}+R_{13}+R_{12})}{R_{23}+R_{13}+R_{12}}$

$R_1 + R_2 + \frac{R_1R_2}{R_{12}} = R_{12}$

QED

Find the equivalent resistance in the given circuit diagram (in terms of $R$)-

---

In order to solve this question, we will transform the circuit and apply the formula side by side-

Notice the highlighted area in the circuit, and then observe the change. Can you identify this transformation (Is it Star-to-Delta or Delta-to-Star)?

Next we will do the same to the other side of the circuit. It will look like this-

Now observe-

Congratulations! We have transformed a complex looking circuit into a simple circuit we can easily solve.

Wasn't that easy? Note that the method shown in this example is not the only way to solve the question. Try transforming other points, make your own way.

Overall answer to the question is $\boxed{\frac{2R}{3}}$.

Now we are capable of solving questions related to transformation of resistances.