Area of a Triangle

There are many different formulas that one can use to calculate the area of a triangle.

This is the most common formula used and is likely the first one that you have seen.

For a triangle with base $b$ and height $h$, the area $A$ is given by

$$A = \frac{1}{2} b \times h.\ _\square$$

Observe that this is exactly half the area of a rectangle which has the same base and height. The proof for this is quite trivial, so there isn't much explanation needed. A logical reasoning for this is that you can make two triangles by dropping an altitude for which both halves are each rotated 180 degrees about their hypotenuse's mid-point to form two rectangles. Thus it is clear that the triangles are one half the area of their respective rectangles which have a total area of $bh.$

What is the area of the triangle pictured below?

Since the triangle has a base of 5 and a height of 8, the area is $\frac{1}{2} \cdot 5 \cdot 8 = 20$. $_\square$

Always keep in mind that the base and height are perpendicular. Here are some more examples.

What is the area of the triangle in the figure below?

---

The figure shows that the base is $b=5$ and height is $h=3.$ Therefore, the area is

$$\frac{1}{2}\cdot5\cdot3=\frac{15}{2}. \ _\square$$

In the figure below, the two lines $l_1$ and $l_2$ are parallel. If the area of $\triangle ABC$ is 6, what is the distance between $l_1$ and $l_2?$

---

The figure shows that the base $\big($which is $\overline{AB}\big)$ is $b=4.$ Since lines $l_1$ and $l_2$ are parallel, the distance between them is the triangle's height $h.$ Hence we have $\frac{1}{2}\cdot4\cdot h=6 \implies h=3.$ Observe that even if we choose a different point upon $l_1$ for $C,$ the area will still remain the same. $_\square$

So you thought that the area of a triangle was simply $\frac{bh}{2}$. Well, it turns out that there are many more ways to derive the area of a triangle than that.

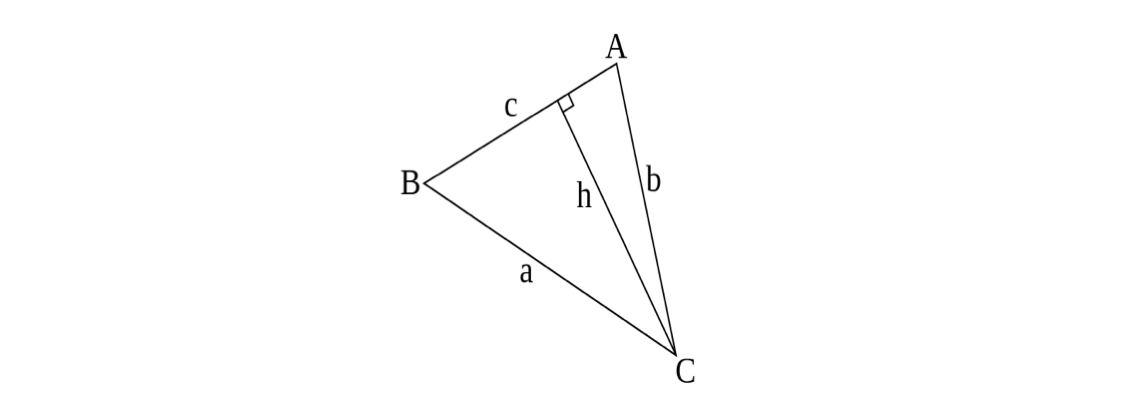
Consider the following triangle with angles $A, B$, and $C$ and corresponding opposite sides $a,b$, and $c$: Then the area of triangle $ABC$ is

$$(\text{Area}) =\frac{1}{2} ab\sin C = \frac{1}{2} bc\sin A = \frac{1}{2} ac\sin B = \frac{abc}{4R},$$

where $R$ is the radius of the circumcircle of triangle $ABC.$ $_\square$

We will prove the area is equal to $\frac{1}{2} bc \sin A$. The other equalities can be proved similarly.

By drawing the height $h$ of the triangle from vertex $C$ to the opposite side, we know that the area of the triangle is

$$(\text{Area}) = \frac{1}{2} ch.$$

Now, $\sin A = \frac{(\text{opposite})}{(\text{hypotenuse})} = \frac{h}{b}$, which implies $h = b\sin A.$ Therefore,

$$(\text{Area}) = \frac{1}{2} ch = \frac{1}{2} c b \sin A.$$

By drawing the height $h$ from the other two vertices, we can similarly show

$$(\text{Area}) =\frac{1}{2} ab\sin C = \frac{1}{2} ac\sin B.$$

To get the last equality, recall that the extended sine rule gives us $\dfrac{a}{\sin A } = 2R$, and hence we get

$$(\text{Area}) = \frac{1}{2} cb \sin A = \frac{ abc } { 4R }.\ _\square$$

For triangle $ABC$, suppose we are given two side lengths $a= 6, b= 5:$

If the area of $\triangle ABC$ is $10,$ what is the value of $\sin C?$

---

By the above formula, the area of the triangle is given by

$$\begin{aligned} (\text{Area}) &= \frac{1}{2} ab\sin C \\ 10 &= \frac{1}{2} \cdot 6 \cdot 5 \sin C\\ \frac{20}{30} &= \sin C\\ \sin C&=\frac{2}{3}. \ _\square \end{aligned}$$

Triangle $ABC$ has side length $a=6$ and angles $\angle A=30^{\circ}$ and $\angle B=45^{\circ}$. Find the area of $\triangle ABC$.

---

Using the law of sines, we have

$$\begin{aligned} \dfrac{a}{\sin{A}}&=\dfrac{b}{\sin{B}}\\\\ \dfrac{6}{\sin{30^{\circ}}}&=\dfrac{b}{\sin{45^{\circ}}}\\\\ \dfrac{6}{\hspace{3mm} \frac{1}{2}\hspace{3mm} }&=\dfrac{b}{\hspace{3mm} \frac{1}{\sqrt{2}}\hspace{3mm} }\\\\ b&=6\sqrt2. \end{aligned}$$

Since the interior angles sum to $180^{\circ}$, $\angle{C}=105^\circ$. Now, using the formula $\frac{1}{2}ab \sin{C}$, we get

$$\begin{aligned} \frac{1}{2} \times 6 \times 6\sqrt2 \times \sin 105^\circ &=18\sqrt{2}\left(\dfrac{\sqrt6+\sqrt2}{4}\right) \\ &=9\sqrt{3}+9. \ _\square \end{aligned}$$

Heron's formula states that the area is $\sqrt{s(s-a)(s-b)(s-c)},$ where $s$ is the triangle's semi-perimeter $\frac{a+b+c}{2}$. A little rearrangement of this yields

$$16A^2=(a+b+c)(-a+b+c)(a-b+c)(a+b-c),$$

where $A$ is the area. $_\square$

Triangle $XYZ$ has all integer side lengths, is inscribed in a circle of radius $25,$ and has side lengths $x=14$ and $y=30$. What is the area of the triangle?

---

We know that the circumradius of the triangle is equivalent to $R=\frac{xyz}{4T}$, where $T$ is the area. We actually proved this above since it's a rearrangement of $\frac{abc}{4R}$.

Plugging in our given values, we have

$$25=\dfrac{(14)(30)z}{4T}\implies 100T=420z.$$

The semi perimeter is $\frac{14+30+z}{2}$, so by Heron's formula $T$ becomes

$$\begin{aligned} T&=\sqrt{\left(22+\frac{z}{2}\right)\left(8+\frac{z}{2}\right)\left(-8+\frac{z}{2}\right)\left(22-\frac{z}{2}\right)}\\ &=\sqrt{\left(484-\frac{z^2}{4}\right)\left(\frac{z^2}{4}-64\right)}\\ &=\frac{1}{4} \sqrt{-z^4+2192z^2-495616}. \end{aligned}$$

Plugging in this value of $T$ yields

$$25\sqrt{-z^4+2192z^2-495616}=420z.$$

Some bashing yields $z=40,$ and plugging in our values into the equation, we have

$$(\text{Area})=\dfrac{abc}{4R}=\dfrac{(14)(30)(40)}{4(25)}=168. \ _\square$$

The proof of this is a little bit tricky, so I'll try to make it as simple as possible.

Begin with an arbitrary triangle $ABC$ with base $c$. Drop the altitude from angle $C$ to side $c$ and call it $h$. Let the two segments of side $c$ be $m$ and $n$ such that there are two right triangles $ANH$ and $BHM$ with sides $a$ and $b$ being their respective hypotenuses. Thus, the area of this triangle is $\frac{1}{2}ch$.

Since $m=c-n$, it follows that $m^2=c^2-2cn+n^2$. Now, keeping that in mind, let's shift gears a bit.

By the Pythagorean theorem, $b^2=h^2+m^2$ and $a^2=h^2+n^2$. Getting back to our original equation, we add $h^2$ to both sides to get

$$m^2+h^2=c^2-2cn+n^2+h^2.$$

Substituting in our Pythagorean equations above for $h^2+n^2$ and $h^2+m^2$, we get $b^2=c^2-2cn+a^2.$ Isolating $n$ gives $n=\frac{a^2+c^2-b^2}{2c}.$

Now, since $h^2=a^2-n^2$, we can substitute our value of $n$ to obtain

$$\begin{aligned} h^2 &= a^2-\left(\dfrac{a^2+c^2-b^2}{2c}\right)^2\\\\ &= \left(a-\dfrac{a^2+c^2-b^2}{2c}\right)\left(a+\dfrac{a^2+c^2-b^2}{2c}\right)\\\\ &=\left(\dfrac{2ac-a^2-c^2+b^2}{2c}\right)\left(\dfrac{2ac+a^2+c^2-b^2}{2c}\right)\\\\ &=\dfrac{\left(b^2-(a-c)^2\right)\left((a+c)^2-b^2\right)}{4c^2}\\\\ &=\dfrac{(b-a+c)(b+a-c)(a+c-b)(a+c+b)}{4c^2}\\\\ \Rightarrow h&=\dfrac{\sqrt{(b-a+c)(b+a-c)(a+c-b)(a+c+b)}}{2c}. \end{aligned}$$

Plugging this into our first equation $(\text{Area})=\frac{1}{2}ch$, we get

$$\begin{aligned} &\frac{1}{2}c\left( \dfrac{\sqrt{(b-a+c)(b+a-c)(a+c-b)(a+c+b)}}{2c}\right)\\\\ &=\dfrac{\sqrt{(b-a+c)(b+a-c)(a+c-b)(a+c+b)}}{4}. \end{aligned}$$

Substituting $s=\frac{a+b+c}{2}$, we get

$$\begin{aligned} \dfrac{\sqrt{2(s)\cdot 2(s-a)\cdot 2(s-b)\cdot 2(s-c)}}{4} &=\dfrac{4\sqrt{(s)\cdot (s-a)\cdot (s-b)\cdot (s-c)}}{4}\\ &=\sqrt{s(s-a) (s-b) (s-c)}. \ _\square \end{aligned}$$

The area of a triangle, given the coordinates of its vertices, is equal to the absolute value of

$$\frac 12 \det \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} .$$

(The sign is positive if the points are given in clockwise order, and negative if they are in counterclockwise order.)

Upon expansion, we get $\frac{1}{2}|x_1y_2-x_3y_2+x_3y_1-x_1y_3+x_2y_3-x_2y_1|.$

If the triangle is in three dimensions, then the area becomes

$$\dfrac{1}{2} \sqrt{\left( \det\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix}\right)^2 + \left( \det \begin{vmatrix} x_1 & z_1 & 1 \\ x_2 & z_2 & 1 \\ x_3 & z_3 & 1 \end{vmatrix}\right)^2 + \left( \det \begin{vmatrix} z_1 & y_1 & 1 \\ z_2 & y_2 & 1 \\ z_3 & y_3 & 1 \end{vmatrix}\right)^2}.$$

Or, it is simply the absolute value of

$$\frac 12 \det \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix} .\ _\square$$

The coordinates of the vertices of a triangle are given to be $A=(1,7), B=(4,5), C=(10,12)$. Find the area of triangle $ABC$.

---

We have

$$\begin{aligned} (\text{Area}) &=& \frac12 \begin{vmatrix}1 & 7 & 1 \\ 4 & 5 & 1 \\ 10 & 12 & 1 \end{vmatrix} \\ &=& \frac12 \big[ (1\cdot5 + 4\cdot12 + 10\cdot7) -(4\cdot7+5\cdot10+12\cdot1) \big] \\ &=& 16\tfrac12.\ _\square \end{aligned}$$

Triangle $ABC$ exists in the 2D Cartesian plane and has two vertices at points $A=(2,3)$ and $B=(-3,9)$. Point $C$ exists on the parabola $y=x^2-1$ such that the $x$-coordinate of point $C$ satisfies $-3<x<3$. Find the maximum possible area of triangle $ABC$.

---

We begin by plugging in our givens: $\frac{1}{2}\big|(2-x_c)(9-3)-(2+3)(y_c-3)\big|.$

Substituting $y=x^2-1$ and expanding, we get $\frac{1}{2}\big|(x-2)(5x+13)\big|.$

Using $\frac{-b}{2a}$, the maximum occurs at $x=-\frac{3}{10}$.

However, since this is an absolute value equation and both roots occur between $-3$ and $3$, we must check to see which value of $x={-3,3,-\frac{3}{10}}$ maximizes the function. Thus, after a little plugging and chugging, we find that $x=\frac{3}{10}$ yields the greatest value for the area of triangle $ABC,$ which is $\frac{529}{40}.$ $_\square$

There are several elegant proofs for this that use vector cross products, determinants, and calculus. However, since this is a wiki on geometry, I will post the simplest geometric proof. Unfortunately, even though this is the simplest, it's also the ugliest.

For simplicity's sake, denote $x_1=a, ~ x_2=b,~ x_3=c,~ y_1=d, ~ y_2=e, ~ y_3=f$.

By this we have coordinates $(a,d), (b,e), (c,f)$. (I know this isn't proper, but trust me, it gets ugly.) Our formula is now $\frac{1}{2}\big|(a-c)(e-f)-(a-b)(d-f)\big|.$

Next, by the distance formula, we have the following:

From $(a,d)$ to $(b,e)$, we get $\sqrt{(a-b)^2-(d-e)^2}$, and set this equal to $p.$
From $(a,d)$ to $(c,f)$, we get $\sqrt{(a-c)^2-(d-f)^2}$, and set this equal to $q.$
From $(b,e)$ to $(c,f)$, we get $\sqrt{(b-c)^2-(e-f)^2}$, and set this equal to $r.$

By Heron's formula, we get $16T^2=(p+q+r)(-p+q+r)(p-q+r)(p+q-r).$

After massive expansion by plugging in our givens $p, q,$ and $r$, we get

$$16T^2=4(b d-c d-a e+c e+a f-b f)^2,$$

which can be factored to

$$(a-c)(e-d)-(a-b)(f-d).$$

Note that $\sqrt{x^2}=|x|.$ Thus, after square rooting both sides, we get

$$|T|=\frac{1}{2}\big|(a-c)(e-d)-(a-b)(f-d)\big|. \ _\square$$

Now that you have learned all of the different possible formulas, let's look at some examples.

If the two side lengths of a triangle are given to be 10 and 11, what is the maximum possible area of this triangle?

---

Since the formula of the area of the triangle is $\frac12 ab \sin C$ with $0 < \sin C \leq 1$, the maximum area occurs at $\sin C = 1$. So the area is $\frac 12 \cdot 10 \cdot 11 \cdot 1 = 55. \ _\square$

Note that the area is maximized when the triangle is a right triangle.

Determine the area of a triangle with side lengths $6,7,8$.

---

Let the side lengths be denoted as $a=6,b=7,c=8$ with the angle opposite to side length $a$ being $A$. By the cosine rule, we have $a^2 = b^2 + c^2 - 2bc \cos A$. Solving for $A$ yields $\cos A\approx \frac{11}{16}$ or $\sin A = \sqrt{1 - \cos^2 A} = \frac{\sqrt{135}}{16}$. Note that we are only taking the positive square root because the sine of any angle of a triangle is non-negative.

Hence, the area is

$$(\text{Area}) = \frac12 bc \sin A = \frac12 \cdot 7 \cdot 8 \cdot \frac{\sqrt{135}}{16} =\frac74 \sqrt{135} \approx 20.333. \ _\square$$

Note that we can also get the area of this triangle using Heron's formula: $(\text{Area}) = \sqrt{s(s-a)(s-b)(s-c)}.$

In geometry, Heron's formula states that the area of a triangle whose sides have lengths $a$, $b$, and $c$ is

$$A = \sqrt{s(s-a)(s-b)(s-c),}$$

where $s$ is the semiperimeter of the triangle, that is,

$$s = \frac{a+b+c}{2}.$$

Heron's formula can also be written as

$$\begin{aligned} A &=& \frac{1}{4}\sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)} \\ &=&\frac{1}{4}\sqrt{2\left(a^2 b^2+b^2c^2+c^2a^2\right)-\left(a^4+b^4+c^4\right)} \\ &=& \frac{1}{4}\sqrt{\left(a^2+b^2+c^2\right)^2-2\left(a^4+b^4+c^4\right)} \\ &=& \frac{1}{4}\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^2}. \end{aligned}$$

Two other area formulas have the same structure as Heron's formula but are expressed in terms of different variables.

First, denoting the medians from sides $a$, $b$, and $c$ respectively as $u, v$ and $w$ and their semi-sum as

$$\sigma = \frac{u+v+w}{2},$$

we have

$$A = \frac{4}{3}\sqrt{\sigma(\sigma-u)(\sigma-v)(\sigma-w)}.$$

Next, denoting the altitudes from sides $a$, $b$ and $c$ respectively as $p$, $q$, and $r$, and denoting the semi-sum of the reciprocals of the altitudes as

$$H = \frac{p^{-1}+q^{-1}+r^{-1}}{2},$$

we have

$$A^{-1} = 4 \sqrt{H\left(H-p^{-1}\right)\left(H-q^{-1}\right)\left(H-r^{-1}\right)}.$$

Other formulae include

• $\frac {1}{2} b h,$ where $b$ is the base and $h$ is the height;
• $\frac {1}{2} a b \sin C,$ where $C$ is the angle, with arms $b$ and $c;$
• $\frac {abc}{4R},$ where $R$ is the circumradius;
• $rs,$ where $r$ is the inradius and $s$ is the semi-perimeter;
• Pick's theorem for the area of a lattice polygon.