Unrolled Linked List
An unrolled linked list is a linear data structure that is a variant on the linked list. Instead of just storing 1 element at each node, unrolled linked lists store an entire array at each node.
Unrolled linked lists combine the advantages of the array (small memory overhead) with the benefits of linked lists (fast insertion and deletion) to produce vastly better performance. By storing multiple elements at each node, unrolled linked lists effectively spread out the overhead of linked lists across multiple elements. So, if an unrolled linked list stores an array of 4 elements at each node, its spreading the linked list overhead (pointers) across those 4 elements.
They have faster performance when you consider the cache management of modern CPUs. Unrolled linked lists have a fairly high overhead per node when compared to the regular, singly linked list. Typically, though, this drawback is small compared to its benefits in modern computing.
Properties
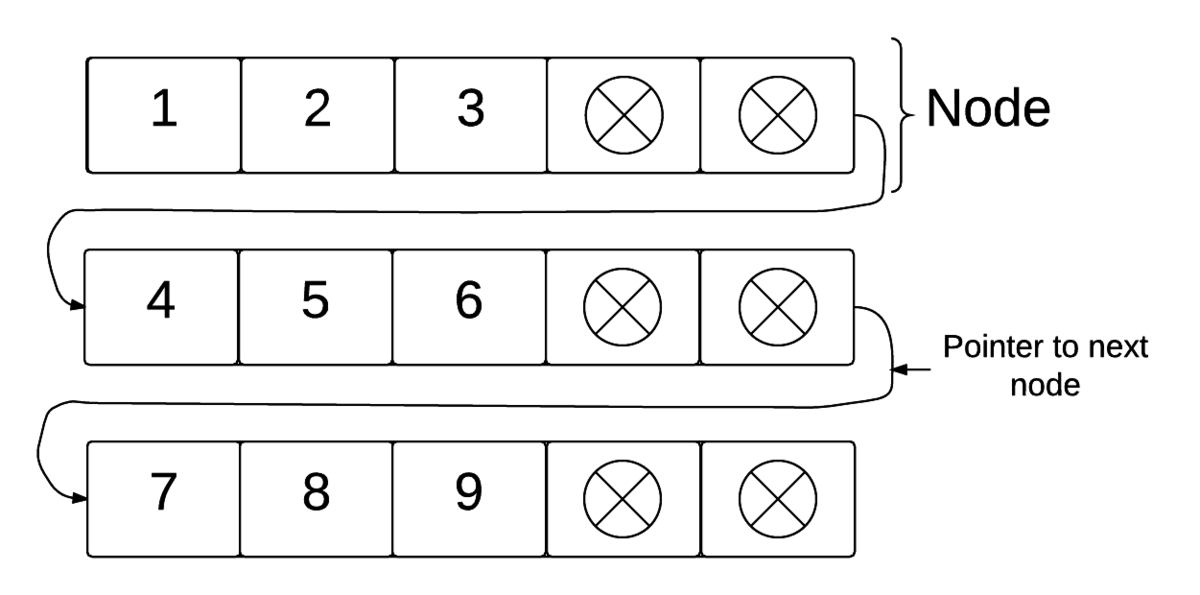 Unrolled Linked List
Unrolled Linked List
The unrolled linked list is essentially a linked list where the node holds an array of values instead of just a single value. The array at each node can hold anything that a typicaly array can such as primitive types and other abstract data types. Each node has a maximum number of values it can hold, and typical implementations keep each node at around an average of \(3/4\) capacity. It does this by moving values between arrays when certain arrays get too full.
The overhead for the unrolled linked list is bit larger per node - now each node has to also store the maximum number of values its array can hold. However, when analyzed on a per value basis, it is much lower than the regular linked list. As the maximum size of the array in each node increases, the average storage space needed per value drops. When the type of value is very small (say, a bit), the space advantages are even greater.
In essence, the unrolled linked list combines the array and the linked list. It takes advantage of the ultra fast indexing and locality of storage of the array. Both of these benefits stem from the underlying properties of static arrays. Plus, it keeps the advantage of insertion and deletion of nodes that the linked list offers.
Insertion and Deletion
The algorithm by which you insert and delete an element in an unrolled linked list can vary from implementation to implemention. Typically, the low-water mark is at 50% - meaning that if an insertion happens in a node that cannot fit the element, a new node is created and half of the original node's elements are inserted into it. Conversely, if we remove an element and the number of values in that node drop below 50%, we move elements from the neighboring array over to fill it back up above 50%. If that array also drops below 50%, we merge the two nodes.
In general, this puts the average node at around 70-75% utilization. Compared with the linked list, the overhead is quite small with a reasonable node size. A linked list requires around 2 or 3 pieces of overhead per node. The unrolled linked list amortizes this overhead across its elements, giving it \(1/size\) which comes close to the overhead of an array.
You can change the low-water mark to change the performance of your unrolled linked list. By increasing it, you would increase the average utilization of each node. However, this will come at the cost of more frequent splitting and merging.
Algorithm Pseudocode
The algorithm for insertion and deletion proceeds as follows. In this example, each Node has an array data, a number of elements currently in that array numElements, and a pointer to the next node next.
1 2 3 4 5 6 7 8 9 10 11 | |
1 2 3 4 5 6 7 8 9 10 11 | |
For both of these functions, many liberties can be taken by the programmer. For instance, in Insert, deciding in which node to try the insertion is up to the programmer. It can be the first node, it can be the last node, or it can be predicated upon some sorting or grouping you wish to maintain. Typically it will be specific to the kind of data you will be working with.
Time and Space Complexity
Unrolled linked lists are difficult to analyze because they are implemented in so many different ways and with some many different variations depending on data. However, they have good time and space analyses due to their amortization across elements.
Time
To insert an element, you must first find the node in which you want to insert. This is \(O(n)\). If that node is not full, you are done. If it is full, you must create a new node and move values over. This process does not depend on total values in the linked list, so it is constant time. Deletion works the same way, in the reverse fashion. We take advantage of these constant time operations due to the fact that linked lists can update their pointers between one another relatively quickly, independent of the size of the linked list.
Indexing is another important quality of the unrolled link list. However, it is highly dependent on caching, which we will cover below.
| Operation | Complexity |
| insertion | \(O(n)\) |
| deletion | \(O(n)\) |
| indexing | \(O(n)\) |
| search | \(O(n)\) |
For unrolled linked lists, it's important to remember that the true benefits come in the form of practical application, not necessarily asymptotic analysis.
Space
The space needed for an unrolled linked list varies from \((v/m)n\) to \(2(v/m)n\) where \(v\) is the overhead per node, \(m\) is the maximum elements per node, and \(n\) is the number of nodes. While this, in the end, equates to the same asymptotic space as other linear data structures like the linked list, it's important to know that it is better because it spreads that overhead over many elements.
| Complexity | |
| space | \(O(n)\) |
Caching
The true benefits of the unrolled linked list come in the form of caching. The unrolled linked list takes advantage of this when it comes to indexing.
When a program access some data form memory, it pulls the entire page. If the program does not find the correct value, we call that a cache miss. This means we can index an unrolled linked list in at most \(m/n + 1\) cache misses. This is up to factor of \(m\) faster than a regular linked list.
We can further analyze this by taking into account the size of cache line, which we will call \(B\). Oftentimes, the size of each node's array, \(m\), will be equal to or be a multiple of the cache line size to optimize the fetching process. In this analysis, each node can be traversed in \((n/B)\) cache misses, so we can traverse the list in \((m/n + 1)(n/B)\). This is very close to the optimial cache miss value of \((m/B)\).