ZFC
ZFC, or Zermelo-Fraenkel set theory, is an axiomatic system used to formally define set theory (and thus mathematics in general).
Specifically, ZFC is a collection of approximately 9 axioms (depending on convention and precise formulation) that, taken together, define the core of mathematics through the usage of set theory. More formally, ZFC is a predicate logic equipped with a binary relation \(\in\), which refers to set membership and is read as "in". To be clear, it is said that \(a \in b\) when \(a\) is an element of \(b\).
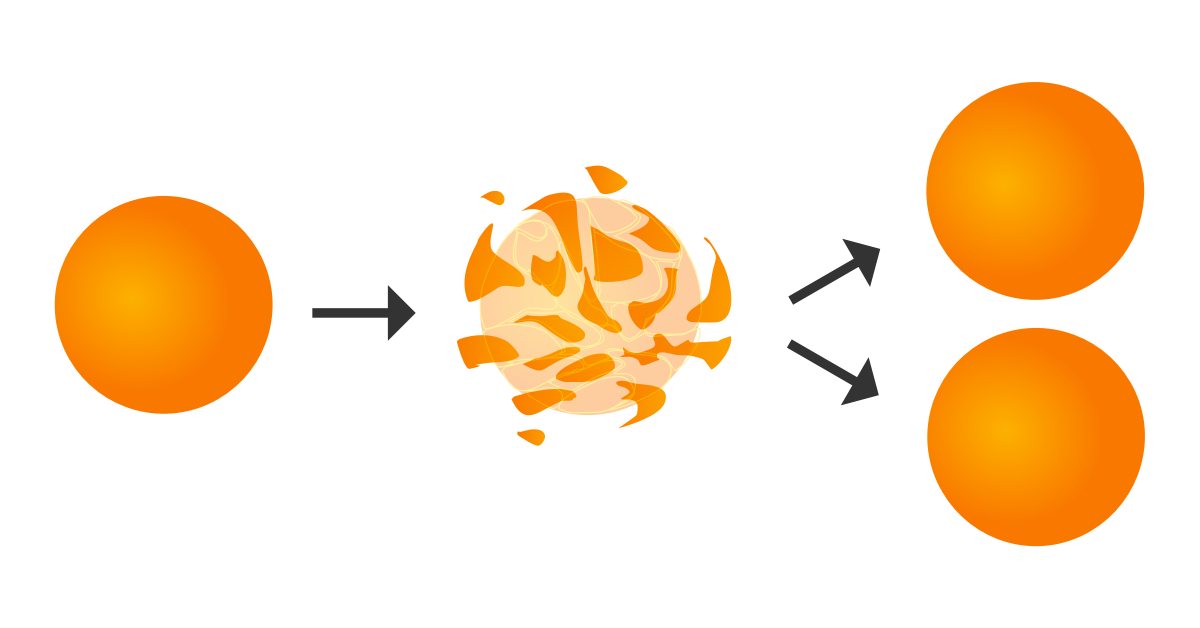 The Banach-Tarski paradox, in which a ball can be rearranged into two balls of the same size as the original, is a counterintuitive consequence of the axiom of choice.
The Banach-Tarski paradox, in which a ball can be rearranged into two balls of the same size as the original, is a counterintuitive consequence of the axiom of choice.
Historically, ZFC was formulated as a means of defining set theory in such a way that paradoxes such as Russell's paradox are avoided, though there remain some unsatisfactory aspects of the theory: in particular, it can be shown that the axiom of choice is independent of the remaining axioms, and thus ZFC with the axiom of choice omitted is still a consistent theory. This is denoted ZF and, while consistent, it has fallen out of use in favor of the more natural ZFC.
Notation
In general, statements in set theory are expressed using first-order logic, which uses a number of quantifiers (or logical symbols):
- \(\in\) means "is in", as in the introduction.
- \(\forall\) means "for all"; e.g. \(\forall n \in \mathbb{R}: n^2 \geq 0\) \(\big(\)translated: for all real \(n\), \(n^2 \geq 0\big)\) is a way of expressing the trivial inequality.
- \(\exists\) means "there exists"; e.g. \(\forall x \in \mathbb{R}\ (\exists y \in \mathbb{R}: y^3 = x)\) \(\big(\)translated: for all real \(x\), there exists a real \(y\) such that \(y^3 = x\big)\) is a way of stating that every real number has a real cube root.
- \(\equiv\) means "is equivalent to". For example, \(x^3>0 \equiv x>0\) is a way of expressing the fact that \(x^3\) is positive if and only if \(x\) is positive.
- \(\implies\) means "implies". For example, \(x>0 \implies x^2>0\) is a way of expressing the fact that the square of a positive number is positive. Note that \(x>0 \not\equiv x^2>0\), since \(x^2>0 \implies x>0\) is a false statement \((\)e.g. for \(x = -1).\)
- \(\land\) means "logical and"; e.g. \(n^2 > 0 \land n^3 < 0\) is a way of expressing the fact that \(n^2\) is positive and \(n^3\) is negative; i.e. \(n\) is negative.
- \(\lor\) means "logical or"; e.g. \(n > 0 \lor n^3 \leq 0\) is a way of saying that either \(n\) is positive or \(n^3\) is nonpositive.
This allows for the axioms in ZFC to be stated succinctly using symbols, as in the following section.
Formal Definition (Axioms)
The axioms of ZFC can be stated in several equivalent ways, and have slightly different names and logical formulations depending on the source. Of course, each individual source will have a rigorous correct treatment of the axioms, one of which follows:
Axiom of extensionality: \[\forall u(u \in X \equiv u \in Y) \implies X = Y\]
In other words, if \(u \in X \iff u \in Y\) for all \(u\), then \(X = Y\). In plain language, this statement is equivalent to "If two sets have the same elements, they are the same set."
Axiom of pairing: \[\forall a \forall b \exists z \forall x\big(x \in z \equiv (x = a \lor x = b)\big),\] where \(\lor\) denotes the logical or quantifier.
In other words, for all \(a\) and \(b\), there exists a \(z\) such that for all \(x\), \(x \in Z\) is equivalent to the statement "\(x = a\) or \(x = b\)". In plain language, this statement is equivalent to "Given two elements, there exists a set containing exactly those two elements."
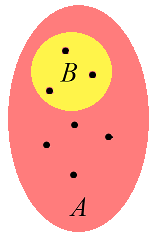 Axiom of comprehension: the elements of \(A\) satisfying \(\phi\) form a new set \(B\)
Axiom of comprehension: the elements of \(A\) satisfying \(\phi\) form a new set \(B\)
Axiom of comprehension: \[\forall X \forall p \exists Y \forall u \left(u \in Y \equiv \big(u \in X \land \phi(u, p)\big)\right),\] where \(\land\) is the logical and quantifier, and \(\phi\) is an arbitrary property.
In plain language, this statement is equivalent to "Given any property \(\phi\) and set \(X\), there exists a set containing all elements of \(X\) that satisfy \(\phi.\)" In informal terms, a subset of a set can be constructed by a succinct rule; e.g. the rule "\(x\) even" applied to the set of integers results in a new set.
Axiom of union: \[\forall X \exists Y \forall u\big(u \in Y \equiv \exists z(z \in X \land u \in z)\big),\] where \(\land\) is the logical and qualifier.
In other words, for all \(X\) there exists a \(Y\) such that for all \(u\), \(u \in Y\) is equivalent to the statement "There exists \(z\) such that \(z \in X\) and \(u \in z.\)" In plain language, there exists a set \(Y\) consisting of the union of all elements of \(X\).
Axiom of power set: \[\forall X \exists Y \forall u\big(u \in Y \equiv u\subseteq X\big)\]
In other words, for any set \(X\), there exists a set \(Y\) whose elements are subsets of \(X\). In plain language, this axiom states that the power set of \(X\) exists.
Axiom of infinity: \[\exists S\left(\emptyset \in S \land \big(\forall x \in S(x \cup \{x\} \in S)\big)\right)\]
In simpler terms, an infinite set exists.
Axiom of replacement: If \(F\) is any function, then for any set \(X\) there exists a set \(Y = F(X) = \{F(x), x \in X\}\). The statement in logical quantifiers is more complex.
 A function takes any set \(A\) to a new set \(B=F(A)\)
A function takes any set \(A\) to a new set \(B=F(A)\)
Axiom of regularity: \[ \forall S\big(S \neq \emptyset \implies (\exists x \in S: S \cap x = \emptyset)\big)\]
In other words, for all non-empty sets \(S\), there exists an element of \(S\) that is disjoint with \(S\) (shares no elements with \(S\)). This has two major consequences:
- No set can be an element of itself. This resolves Russell's paradox.
- Every set has a smallest element with respect to \(\in\).
These 8 axioms define a consistent theory, ZF (though, of course, it is very difficult to prove that this system is consistent). When the axiom of choice is added to the eight axioms above, the theory becomes ZFC (the "C" for choice), and it is this system that is commonly used as the foundation of mathematics.
Advantages and Disadvantages
ZFC is only one of many axiomatic systems that can be used as the formulation of mathematics, and as such has certain advantages and disadvantages over other similar systems.
The main advantage of ZFC is to facilitate the study of set theory itself, though from certain perspectives this is a disadvantage as well. In particular, most of modern mathematics can be proven in weaker axiomatic systems like the Peano axioms, and all of it can be carried out in ZC: Zermelo set theory with the axiom of choice (Zermelo theory is obtained from dropping the axiom of replacement). Thus, in some sense, ZFC is "too strong" for the sake of making set theory easier.
On the other hand, another common criticism is that ZFC is too weak when compared to other axiomatic systems. For instance, the continuum hypothesis (along with a handful of other problems) can be shown to be independent of ZFC, meaning that it can be neither proved nor disproved with the given axioms. Thus some choose to adopt various extensions of ZFC, or closely related systems such as ZF+AD--where the axiom of choice is replaced by the axiom of determinacy.
Additionally, there are a number of objections to set theory in general (see the set theory page for details).