Activation Energy
Consider a situation as in the image below. You have to roll a heavy metallic ball up the hill with a truck. To roll the ball to the other side, you first have to roll it over the top of the hill. We can do this by converting the kinetic energy of the truck into potential energy.

When you start with less kinetic energy than what it is required to overcome friction and potential energy, you will be unable to roll the ball over the hilltop and the kinetic energy will either be lost due to friction (e.g. if you apply the brakes from the truck) or as kinetic energy due to the ball rolling down the hill.
The exact same thing occurs during a chemical reaction. For a reaction to occur, the reactant must collide with each other with some minimum amount of energy to break old bonds and to form new bonds. This energy requirement is fulfilled by the kinetic energy of reacting molecules as they are always travelling in a continuous and random direction. If the reactant has less kinetic energy than is required to cross this energy barrier, nothing will happen and they will lose it by Brownian motion and friction. This minimum energy requirement is known as the activation energy of a reaction.
Given below is the energy profile for a hypothetical reaction \(A+B\to AB.\)

Activation energy is the difference in the energy of the reactants and an activation complex also known as the transition complex. Any energy in this intermediate or transition complex represents the energy barrier. If the reacting molecules have higher energy than the energy barrier, then they will react to form product AB.
Arrhenius Equation and Activation Energy
The Arrhenius equation gives a quantitative relationship between the rate of reaction, temperature, and activation energy with the following formula:
\[k=Ae^{-E_a/RT},\]
where
- \(k\) is the rate constant;
- \(A\) is the pre-exponential factor, a constant for every chemical reaction;
- \(E_a\) is the activation energy of the reaction;
- \(R\) is the universal gas constant;
- \(T\) is the absolute temperature in Kelvin.
To evaluate activation energy, one needs to have a rate versus temperature profile. The final formula to be used can be derived as
\[\begin{align} k&=Ae^{-E_a/RT}\\ \ln(k)&=\frac{E_a}{RT}-\ln(A). \end{align}\]
This equation has a linear form of \(y=mx+c\). Plotting a graph between \(\ln(k)\) and \(\frac{1}{T}\), the value of the slope will be
\[m=-\frac{E_a}{R}.\]
For a first-order reaction \(A \to B\), the temperature\((T)\)-dependent rate constant \((k)\) was found to follow the equation
\[\log k=-(2000)\frac{1}{T}+6.\]
Which of the following correctly states the respective values of the pre-exponential factor in \(\text{s}^{-1}\) and the activation energy \(E_a\) in kJ/mol?
To solve this problem, you need to know activation energy.
\[\large k = A e^{-\frac{E_a}{RT}}\]
The Arrhenius equation above tell us how the rate constant \(k\) for a particular reaction depends on its activation energy \(E_a\) and temperature \(T:\)
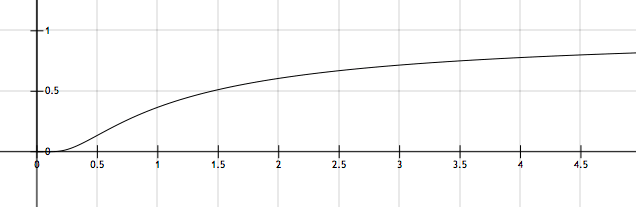
The figure above shows a typical plot of \(k\) versus \(T\). If the corresponding value of \(k\) for the point of inflection for the curve above is given by \(k' = A e^X\) for some constant \(X,\) then find \(|X|.\)
Assumptions and Clarifications:
- The pre-exponential factor or \(A\) for the given reaction is essentially a constant.
- \(R=8.314 \text{ J/(K mol)}\) is the gas constant.
How does a Catalyst Work?
A catalyst increases the rate of reaction. How a catalyst does this can be explained by the concept of activation energy. We have seen that activation energy represents the energy barrier. More activation energy means that the reaction from the reactants to the product is more difficult. A catalyst provides an alternative pathway for a reaction to occur, consisting of one or several intermediate or transition complexes.

In the case of a reversible reaction, a catalyst does not disturb the equilibrium. Instead, it increases the rate constant of both forward and backward reactions to the same extent so that their ratio, which is the equilibrium constant \(K_c\), remains unchanged. Hence, equilibrium is attained faster than an uncatalyzed reaction.
It is worth recalling what activation energy is. Activation energy is the difference between the energy of a transition state and the energy of a reactant or reactants. With this in mind, the activation energy for a backward reaction will be the difference between the energy of a product and the transition state. This is because, in a backward reaction, the product becomes the reactant.
Let
- \(E_{af}\) be the activation energy for a forward reaction in an uncatalyzed reaction;
- \(E_{ab}\) be the activation energy for a backward reaction in a catalyzed reaction;
- \(E_{afc}\) be the activation energy for a forward reaction in an uncatalyzed reaction;
- \(E_{abc}\) be the activation energy for a backward reaction in a catalyzed reaction.
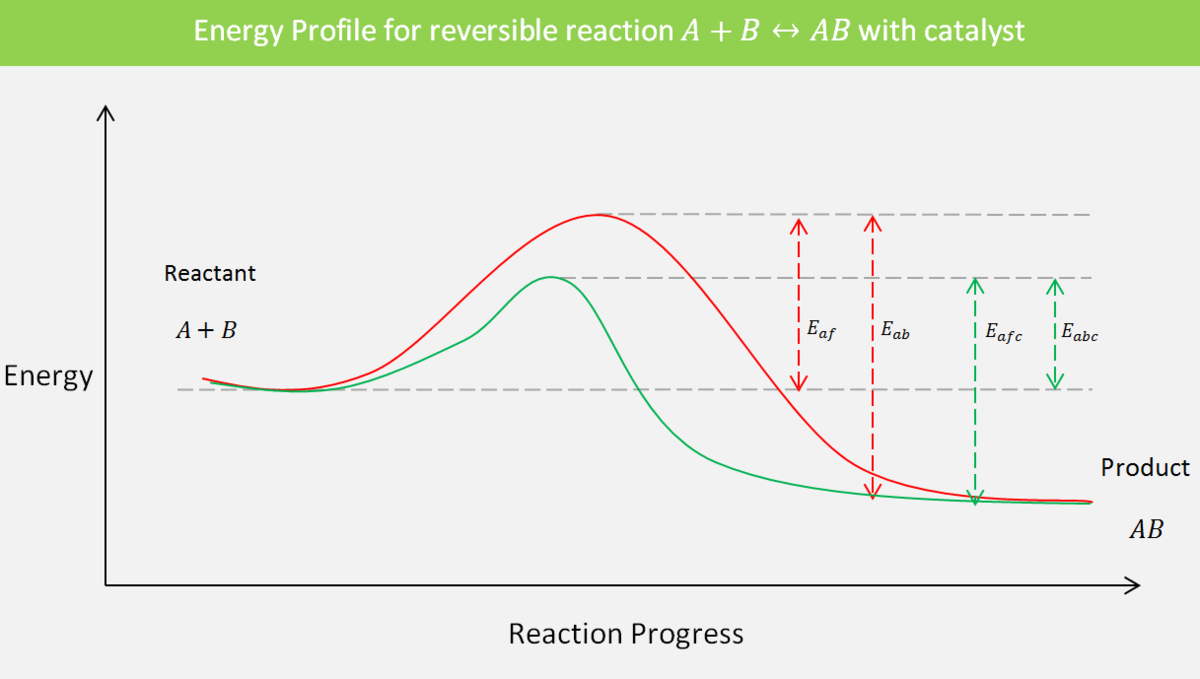
Let's calculate the equilibrium constant for a catalyzed and an uncatalyzed reaction. We have the Arrhenius equation which relates the rate constant and activation energy:
\[k_f=Ae^{-E_{af}/RT},\]
where \(A\) is the pre-exponential factor.
Similarly, for backward reactions,
\[k_b=Ae^{-E_{ab}/RT}.\]
So, the equilibrium constant is given by
\[K=\frac{k_f}{k_b}=\frac{Ae^{-E_{af}/RT}}{Ae^{-E_{ab}/RT}}=e^{-(E_{af}-E_{ab})/RT}.\]
Similarly, in calculating the equilibrium constant for a catalyzed reaction, we have
\[K_c=e^{-(E_{afc}-E_{abc})/RT}.\]
Since \(E_{af}-E_{ab}=E_{afc}-E_{abc}\),
\[K=K_c.\]
Inhibitors
Inhibitors are chemical compounds which reduce the rate of reaction. They do not do it by providing a high activation energy pathway because if they do so, the reaction will tend to occur via a non-inhibitor or a normal route as it is more favourable. They do it either by destroying a catalyst or free radicals that are formed during an intermediate step.