Alternate Segment Theorem
The alternate segment theorem (also known as the tangent-chord theorem) states that in any circle, the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.

In the above diagram, the angles of the same color are equal to each other. For easily spotting this property of a circle, look out for a triangle with one of its vertices resting on the point of contact of the tangent to the circle. In this wiki we will be learning this theorem in detail along with proofs and its applications in several arenas with the help of examples.
Contents
Alternate Segment Theorem Statement and Explanation
Let's first get familiar with the definition of alternate segment theorem and then we will understand it by a detailed explanation.
Alternate Segment Theorem
In any circle, the angle between a chord and a tangent through one of the endpoints of the chord is equal to the angle in the alternate segment, i.e. the angle subtended by the chord in the opposite side of the previous angle.
Now let's go through the following explanation to have a clear understanding of the theorem:

To be more explicit, consider the above circle \(\Gamma\) with center \(O\), with a chord \(PT\). A tangent \(T_1T_2\) passes through the point \(T\). Consider any point \(X\) on \(\Gamma\) on the side of \(PT\) opposite to where \(T_1\) is situated. Then we have \(\angle PTT_1=\angle PXT\). For example, if \(\angle PTT_1=37^\circ\) then we have \(\angle PXT=37^\circ\).
What if we arbitrarily move \(X\) on that side of \(PT\)? The statement still remains true because the angle \(\angle PXT\) subtended by minor arc \(PT\) is constant, irrespective of the position of \(X\).
Proofs of Alternate Segment Theorem
In this section we will prove the Alternate Segment Theorem through two different methods.

Consider the above figure. We've taken \(X\) diametrically opposite to \(T\), so \(XT\) passes through \(O\), the center of \(\Gamma\). Let \(\angle PXT=\alpha\) and \(\angle PTT_1=\beta\). We want to prove that \(\alpha=\beta\). Notice that since the angle subtended by a diameter is a right angle, we have \(\angle XPT=90^\circ\). Also since the radius through the touch point is perpendicular to the tangent, we have \(\angle XTT_1=90^\circ\). Now in right angled \(\triangle PTX\), we get \(\alpha = 90^\circ - \angle PTX\). And from the figure we can easily see that \(\beta = \angle XTT_1-\angle PTX=90^\circ - \angle PTX\). Hence \(\alpha=\beta\). \(_\square\)
Note: There is another configuration when the angle at \(X\) is subtended by the major arc \(PT\) (when \(\angle PXT\) is obtuse). This is left to the reader as an exercise.
Here's another proof:
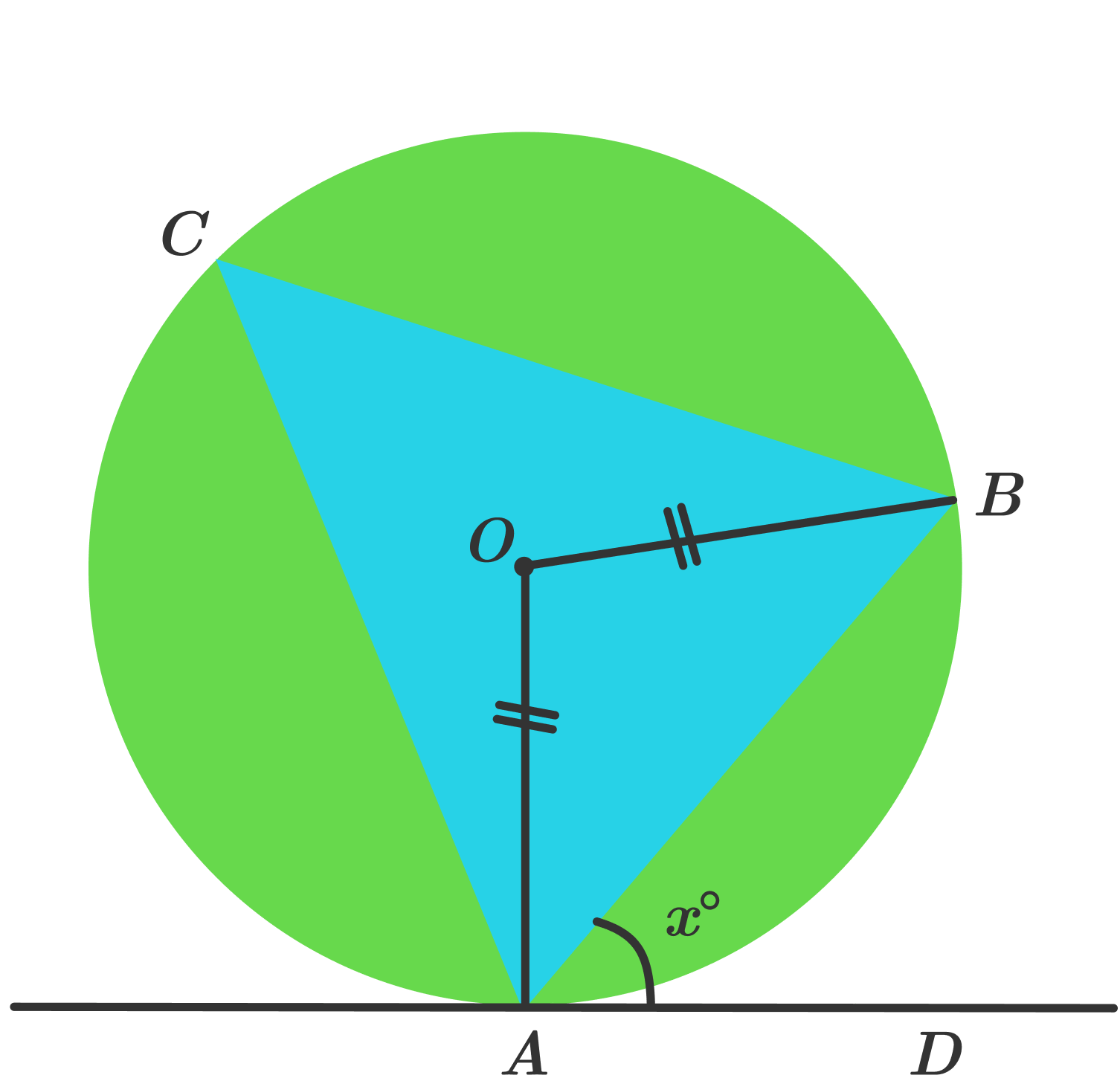
Since \( \overline{OA}\) and \( \overline{OB}\) are both the radii of the circle, \(\lvert \overline{OA}\rvert=\lvert \overline{OB} \rvert .\)
Since \( \triangle AOB\) is isosceles, we have
\[ \begin{align} \angle AOB &= 180^\circ -\angle OAB - \angle OBA\\ &= 180^\circ - 2 \angle OAB. &\qquad (1) \end{align} \]
Since \(\overline{AD}\) is a tangent, we have
\[ \begin{align} \angle OAD &=90^\circ \\ \Rightarrow x^\circ &= 90^\circ - \angle OAB. &\qquad (2) \end{align} \]
Then from \((1)\) and \((2),\) it follows that \[\angle AOB= 2x^\circ.\]
Now, from the properties of an inscribed triangle, we know that \( \angle AOB = 2\angle ACB .\)
Therefore,
\[ \angle ACB = \frac{1}{2} \angle AOB = \frac{1}{2} \cdot 2 x^\circ = x^\circ. \ _\square \]
Example Problems using Alternate Segment Theorem
To ensure that you have mastered this theorem, work through the following examples:

In the above diagram it is given that \( \angle BAD=45^\circ.\) What is \( \angle ACB ?\)
From the tangent-chord theorem, the angle between a tangent and a chord that meet on a circle, is equal to the inscribed angle on the opposite side of the chord. Thus,
\[ \angle ACB = \angle BAD = 45^\circ. \ _\square\]

In the above diagram find the value of \( \angle AOB\), provided that \( \angle BAC \) is \(50^\circ\).
Since \( \angle AOB = 2\times \angle BAC, \) we have
\[ \angle AOB = 2 \times \angle BAC = 2 \times 50^\circ = 100^\circ. \ _\square \]

In the above diagram, \( \angle BAD = 40^\circ\) and \(\angle BAC = 65^\circ .\) What is \( x?\)
According to the tangent-chord theorem, we have
\[ \angle ACB = \angle BAD = 40^\circ. \qquad (1) \]
For \( \triangle ABC,\) the sum of its three internal angles must equal \( 180^\circ.\) Thus, from \( (1),\) it follows that
\[ \begin{align} \angle ACB + \angle BAC + \angle ABC &= 180^\circ \\ \angle ABC & = 180^\circ - \angle ACB - \angle BAC \\ \angle ABC & = 180^\circ - \angle BAD -\angle BAC \\ \angle ABC &= 180^\circ - 40^\circ - 65^\circ \\ \angle ABC &= 75^\circ. \end{align} \]
Therefore, \( x = 75. \) \(_\square \)
Now it's your turn to solve the following problem:
Find \(X^\circ + Y^\circ.\)

For deeper insights into the theorem, let's work through some more examples:

In the above diagram, \(\overline {BC}\) is tangent to circle \(O,\) where the point of contact is \(B.\) If the radius of circle \(O\) is 10 and \(\alpha ^\circ=50 ^\circ,\) what is the length of the arc \(\widehat{APB}?\)

Since \(\overline {BC}\) is a tangent line, \(\angle OBC=90^\circ,\) implying \(\angle OBA=(90-\alpha)^\circ.\) Then since \(\triangle OAB\) is an isosceles triangle, \(\angle OAB=\angle OBA=(90-\alpha)^\circ.\) This implies\[ \begin{align} \angle AOB &= 180^\circ - \angle OBA - \angle OAB \\ &= 180^\circ - (90-\alpha)^\circ - (90-\alpha)^\circ \\ &= 2\alpha^\circ \\ &= 100^\circ. \end{align} \]
Therefore, the length of the arc \(\widehat{APB},\) denoted by \(\lvert\widehat{APB}\rvert,\) is
\[ \begin{align} \lvert\widehat{APB}\rvert &= 2\pi \times 10 \times \frac{100^\circ}{360^\circ} \\ &= \frac{50}{9}\pi. \ _\square \end{align} \]
The tangents at \(A\), \(B\) to the circumcircle of \(\triangle ABC\) meet at \(T\). The line through \(T\) parallel to \(AC\) meets \(BC\) at \(D\). Prove that \(AD=CD\).
Refer to the figure above. Let's figure out what we know from the problem statement. Since \(AC\parallel TD\) with transversals \(AD\) and \(BC\), we have \(\angle ADT=\angle CAD\) and \(\angle BDT=\angle ACD\). Also \(TA\) and \(TB\) are tangents from the same point \(T\), so \(TA=TB\) and consequently, \(\angle TAB=\angle TBA\). Since there are tangents, we should consider the alternate segment theorem, by which we have \(\angle TAB=\angle ACB\). Combining all these results, we find
\[\angle BDT=\angle ACD=\angle ACB=\angle TAB=\angle TBA, ~~~~~\angle ADT=\angle CAD.\]
In particular, \(\angle TAB=\angle TDB\), so \(ATBD\) is cyclic. Hence \(\angle TBA=\angle ADT\). So we finally have this long chain
\[\angle BDT=\angle ACD=\angle ACB=\angle TAB=\angle TBA=\angle ADT=\angle CAD.\]
In particular \(\angle ACD=\angle CAD\) in \(\triangle ACD\), so \(AD=CD\). \(_\square\)

Triangle \(ABC\) has vertices \(B\) and \(C\) on a semicircle centered at \(O,\) as shown, with \(AB\) tangent to the semicircle at \(B\) and \(AC\) intersecting the semicircle at point \(D.\)
If \(\angle BAC = 78 ^\circ\)(in red) and \(\angle ODC = 74 ^\circ\)(in green), what is the measure of \(\angle BCA\) (in blue) in degrees?
Note: The figure is not drawn to scale.
Circles \(\Gamma_1\) and \(\Gamma_2\) intersect at 2 distinct points \(A\) and \(B\). A line \(l\) through \(A\) intersects \(\Gamma_1\) and \(\Gamma_2\) at points \(C\) and \(D,\) respectively, such that \(C\) is not in \(\Gamma_2\) and \(D\) is not in \(\Gamma_1\). Point \(E\) is the intersection of the tangent to \(\Gamma_1\) at \(C\) and the tangent to \(\Gamma_2\) at \(D\).
If \(\angle CBD = 71^\circ,\) what is the measure (in degrees) of \( \angle CED?\)