Arithmetic Puzzles - Fill in the Blanks
A fill in the blanks problem is a type of arithmetic puzzle in which single digit integers fit into empty spaces so that they satisfy given constraints. These puzzles come in many forms, whether it be an equation, a carefully constructed grid of boxes, or even long divisions. Solving these puzzles by hand requires some logical deduction and understanding the behavior of certain choices of digits subject to various arithmetic operators.
Fill in the boxes with distinct integers 1 to 5 such that the following equation holds true:
\[ \square \, + \, \square \, - \, \square \, \times \, \square \, \div \, \square = 6.\]
Fill in the blank (FITB) puzzles are similar to operator search puzzles, wherein operators are used to complete the puzzle, rather than digits. Throughout this page, the following rules will be observed:
A row of squares \(\underbrace{ \square\square\square \cdots \square }_{n \text{ squares}} \) represents an \(n\)-digit integer with each square containing one digit with the first square being non-zero. It does not represent the multiplication \(\square \,\times\, \square\,\times\,\square \,\times\, \cdots \,\times\, \square. \)
The proper order of operations, BODMAS, is followed.
Contents
Satisfying One Equation
Before jumping into solving FITB equations, we must first know how to interpret these boxes/blank spaces. In this section, we will be teaching you two things: how to convert the given equations to something we're all familiar with, and how to directly interpret these boxes mathematically.
1) Rephrase the equation into a more familiar version \[\]
Like solving a cryptogram, because it is uncommon to write out math expressions in boxes, as a beginner we should always try to rephrase the equation into a more familiar version: formal mathematical notations.
For example, if the boxes below represent distinct integers 6 to 9, how do we fill in the boxes properly?
\[ \boxed{\phantom0}\boxed{\phantom0}\boxed{\phantom0} - \boxed{\phantom0} = 788 \]
For starters, because there are 4 squares and 4 numbers to fill them with, (by rule of product) we could try out all \(4! = 24\) possibilities to find out whether the solution exists. But this will be tedious and exhausting. Then how do we solve this puzzle in a systematic manner? Just convert it to something we're familiar with: algebraic notations!
If we denote the 3-digit integer \(\boxed{\phantom0}\boxed{\phantom0}\boxed{\phantom0}\) and the 1-digit integer \(\boxed{\phantom0} \) as \(x\) and \(y,\) respectively, we obtain the equation \(x-y= 788\). Since there are \(3! = 6\) possible values of \(x\) and 4 possible values of \(y\), it's much simpler to work on the value of \(y\) because there's less possibilities.
- If \(y = 6\), then \(x = 788+ y = 788+ 6 = 794\), implying \( \boxed7\boxed9\boxed4-\boxed6= 788.\) But this doesn't satisfy the constraint that the boxes represent all the integers 6 to 9.
- If \(y = 7\), then \(x = 788+ y = 788+ 7 = 795\), implying \( \boxed7\boxed9\boxed5-\boxed7= 788.\) But this doesn't satisfy the constraint that the boxes represent all the integers 6 to 9.
- If \(y = 8\), then \(x = 788+ y = 788+ 8 = 796\), implying \( \boxed7\boxed9\boxed6-\boxed8= 788.\) This does satisfy the constraint that the boxes represent all the integers 6 to 9.
- If \(y = 9\), then \(x = 788+ y = 788+ 9 = 797\), implying \( \boxed7\boxed9\boxed7-\boxed9= 788.\) But this doesn't satisfy the constraint that the boxes represent all the integers 6 to 9.
Therefore, \(y = 8\) is the only possible solution, so we do know how to fill in the boxes properly!
\[ \boxed7\boxed9\boxed6-\boxed8= 788.\]
\[ \left(\color{green}{\square}5\right)^2 = \color{blue}{\square}25 \]
Each square above represents a positive integer. Let \(m\) and \(n\) denote the values that fill in the green and blue squares, respectively, satisfying the equation. Then what is the relationship between \(m \) and \(n?\)
Details and Assumptions:
- This is an arithmetic puzzle, where \( 1 \square \) would represent the 2-digit number 19 if \( \square = 9 \). It does not represent the algebraic expression \( 1 \times \square \).
Now that we know how to convert the boxes to proper notation and vice versa, let's try something new: an immediate reading of the numbers from the boxes provided. Read the following section!
2) Directly read the boxes as the numbers that they truly are \[\]
After knowing what the boxes represent, we can immediately interpret numbers like \( \boxed{\phantom0} \boxed2\boxed{\phantom0} \) as a 3-digit integer with its tens digit 2. So yes, it may be convenient or easier to convert an FITB equation to something more familiar, but sometimes it is not worth the effort. Let's look at the following equation as an example:
\[ \boxed{\phantom0}\boxed8 \div \boxed3 \boxed{\phantom0} = 2. \]
Do we really need to convert it to an equation with proper notations such as \((10p+8) \div (30+q) = 2\) to solve it? Not necessarily. Here's how we're going to do it:
Multiplying both sides by \(\boxed3 \boxed{\phantom0} \), we get \(\boxed{\phantom0}\boxed8 = 2\times \boxed3 \boxed{\phantom0},\) which implies \(\boxed8\) is the last digit of the value of \(2 \times \boxed{\phantom0}. \) Then we have two possibilities: \(2\times \boxed4 =8 \) or \(2\times \boxed9 =18,\) which is equivalent to \(8\div 4=2\) or \(18\div 9=2,\) respectively.
So now we have \( \boxed{\phantom0}\boxed8 \div \boxed3 \boxed{4} = 2 \) or \( \boxed{\phantom0}\boxed8 \div \boxed3 \boxed{9} = 2 \). Finishing it off yields the desired numbers:
\[ \boxed{6}\boxed8 \div \boxed3 \boxed{4} = 2, \quad \boxed{7}\boxed8 \div \boxed3 \boxed{9} = 2 .\]
Let's try the following example which is a little harder:
Fill in the blanks such that the following equation is satisfied: \[\]
\[ \boxed7 \boxed{\phantom0} \times \boxed{\phantom0} \boxed2 = \boxed{\phantom0} \boxed7 \times \boxed2 \boxed{\phantom0} = 888.\]
Factoring the number 888, we get \(888 = 2^3 \times 3 \times 37. \) Because 888 is written in terms of product of two 2-digit integers, we know that
- at least one of the integers \( \boxed7\boxed{\phantom0}\) and \(\boxed{\phantom0} \boxed 2 \) is divisible by 37; \(\qquad (1)\)
- at least one of the integers \( \boxed{\phantom0}\boxed7\) and \(\boxed 2 \boxed{\phantom0}\) is divisible by 37. \(\qquad (2)\)
The only multiples of 37 that are 2-digit integers are \(37\times1=37 \) and \(37\times2=74\), so
- one of the numbers in \((1)\) is \(74\) and thus the other number is \(888\div74= 12 \);
- one of the numbers in \((2)\) is \(37\) and thus the other number is \(888\div37= 24 \).
Hence the answer is
\[ \boxed7 \boxed{4} \times \boxed{1} \boxed2 = \boxed{3} \boxed7 \times \boxed2 \boxed{4} = 888. \]
Now are you comfortable enough to directly interpret all these boxes? Take a jab at the following problem:
\[ \large \square + \square\square+\square\square\square+\square\square\square\square \]
Place each of the digits 0 through 9, without repetition, in the boxes above. Then what is the maximum possible sum?
Details and Assumptions:
- This is an arithmetic puzzle, where \( 1 \square \) would represent the 2-digit number 19 if \( \square = 9 \). It does not represent the algebraic expression \( 1 \times \square \).
Satisfying an Array of Equations
The previous section shows us how to solve an FITB puzzle for a single equation. Now what if we're given more equations? Does it make the puzzle harder? Well, not quite. It is not so different from solving a system of equations. Since we already have all the fundamentals we need in the previous section, let's get started with an example:
Fill in the boxes below with distinct integers from 1 to 5 such that the array of equations holds true. \[\]
\[ \large{\begin{array}{ccccccc} & & \boxed{\phantom0} & & & & \\ & & - & & & & \\ \boxed{\phantom0} &+& \boxed{\phantom0} & \times &\boxed{\phantom0} & = & 11 \\ & & \div & & & & \\ & & \boxed {\phantom0} & & & & \\ & & = & & & & \\ & & 1 & & & & \\ \end{array}} \]
Let's start with the 2 boxes directly above and below the division sign (\(\div\)), and call them \(X\) and \(Y,\) respectively. Because all of the boxes represent numbers that are integers, \(X\) must be divisible by \(Y.\) Also, \(1\leq X,Y \leq 5\) and \(X\ne Y.\) Thus, the possibilities are \((X,Y) = (4,2),(5,1),(4,1),(3,1), (2,1) \) only.
Let \(Z\) be the number in the box at the top, then we can analyze these 5 possibilities as follows:
If \((X,Y) = (4,2) \), then \(Z - (X\div Y) = 1 \Rightarrow Z = 3 \). So the two unused integers are 1 and 5, which must satisfy the equation \( \boxed{\phantom0} + \boxed4 \times \boxed{\phantom0} = 11 \). Trial and error shows that there is no solution, and thus \((X,Y) = (4,2) \) cannot be a solution.
If \((X,Y) = (5,1) \), then \(Z - (X\div Y) = 1 \Rightarrow Z = 6 \). But since \(Z\) must be an integer between 1 and 5 inclusive, \((X,Y) = (5,1) \) cannot be a solution.
If \((X,Y) = (4,1) \), then \(Z - (X\div Y) = 1 \Rightarrow Z = 5 \). So the two unused integers are 2 and 3, which must satisfy the equation \( \boxed{\phantom0} + \boxed4 \times \boxed{\phantom0} = 11 \). Trial and error shows that \( \boxed{3} + \boxed4 \times \boxed{2} = 11 \), and thus \((X,Y) = (4,1) \) can be a solution.
If \((X,Y) = (3,1) \), then \(Z - (X\div Y) = 1 \Rightarrow Z = 4 \). So the two unused integers are 2 and 5, which must satisfy the equation \( \boxed{\phantom0} + \boxed3 \times \boxed{\phantom0} = 11 \). Trial and error shows that \( \boxed{5} + \boxed3 \times \boxed{2} = 11 \), and thus \((X,Y) = (3,1) \) can be a solution.
If \((X,Y) = (2,1) \), then \(Z - (X\div Y) = 1 \Rightarrow Z = 3 \). So the two unused integers are 4 and 5, which must satisfy the equation \( \boxed{\phantom0} + \boxed4 \times \boxed{\phantom0} = 11 \). Trial and error shows that there is no solution, and thus \((X,Y) = (2,1) \) cannot be a solution.
Therefore, there exist two solutions, namely
\[ \large{\begin{array}{ccccccc} & & \boxed4 & & & & \\ & & - & & & & \\ \boxed5 &+& \boxed3 & \times &\boxed2 & = & 11 \quad \quad \text{and} \quad \quad \\ & & \div & & & & \\ & & \boxed 1 & & & & \\ & & = & & & & \\ & & 1 & & & & \\ \end{array}} \large{\begin{array}{ccccccc} & & \boxed5 & & & & \\ & & - & & & & \\ \boxed3 &+& \boxed4 & \times &\boxed2 & = & 11. \\ & & \div & & & & \\ & & \boxed 1 & & & & \\ & & = & & & & \\ & & 1 & & & & \\ \end{array}} \]
Though the example above takes up more caseworks, we are still able to solve it in a reasonable manner! Are you ready to try another example with an array of equations?
 Using the digits 1 through 9 without repetition, fill out the number grid above. What is the product of the numbers in the 4 corners?
Using the digits 1 through 9 without repetition, fill out the number grid above. What is the product of the numbers in the 4 corners?
Note: The order in which this grid calculates is left-to-right/top-to-bottom unlike the usual order of operations. E.g., \(1+2\times 3 = (1+2)\times3=9.\)
Determining Possible Outputs
Questions involving maximizing/minimizing the value of an expression are among the most common and interesting problems in recreational mathematics. Though there is no fixed rule for these type of puzzles, there are generally three types of techniques that are most often used, as shown below.
| Technique | Brief description |
| 1) Trial and error | This technique practically needs no introduction. Basically we list all possible scenarios and check whether each of them satisfies the constraint. |
| 2) Use of the properties of binary operations | There isn't a need to check out all the cases when the commutative property, associative property, and idempotent property can show us those similar cases. |
| 3) Identifying extremal points | Though this technique varies from case to case, it essentially boils down to finding out which numbers fit into which box such that the resultant number is minimized/maximized. |
Let's look at the following examples that apply these techniques:
\[ \large {\square \times \square + \square \times \square}\]
Fill in the boxes with all the integers 1, 2, 3 and 4 such that the value of the expression is as great as possible.
To solve this problem, we can apply (1) Trial and error to find every possible permutation of the numbers in the equation, and then figure out the greatest value among them. However, because there are a total of \(4!=24\) cases, this method can be tedious.
Noting that the expression above is the sum of multiplications between 2 pairs of numbers, we can apply (2) Use of the properties of binary operations: since \(a\times b = b\times a\) has a commutative property, we do not need to list all 24 cases. Now let's get started.
Let \(a,b,c\) and \(d\) denote the numbers that represent the boxes in that order, i.e. \(ab + cd \). Without loss of generality, we can assume that \(a<b, c<d\), and \(a<c\). Combining these three inequalities shows that \(a \) is the smallest value, and thus \(a=1\) only. Then we just need to check the following 3 cases:
- If \(b = 2\), then \(c = 3\) and \(d = 4\), so we have \( \boxed { 1 } \times \boxed { 2 } +\boxed { 3 } \times \boxed { 4 } =14\).
- If \(b = 3\), then \(c = 2\) and \(d = 4\), so we have \( \boxed { 1 } \times \boxed { 3 } +\boxed { 2 } \times \boxed { 4 } =11 \).
- If \(b = 4\), then \(c = 2\) and \(d = 3\), so we have \( \boxed { 1 } \times \boxed { 4 } +\boxed { 2 } \times \boxed { 3 } =10 \).
Since we have used all combinations of the numbers, we can be sure that the largest possible value of the expression is 14:
\[ \boxed { 1 } \times \boxed { 2 } +\boxed { 3 } \times \boxed { 4 } =14.\]
Did you realize in the example above that we have reduced the number of trials from a staggering 24 cases to mere 3 cases? Note that we've used only the first two techniques but not the third one yet.
Now let's try a problem that forces us to use the third technique.
\[ \Large {\square ^ {\square ^ {\square ^ \square}}}\]
Fill in the boxes with all the integers 1, 2, 3 and 4 such that the value of the expression is as small as possible.
As in the previous example, we can apply (1) Trial and error. However, because there are a total of \(4!=24\) cases, this method can again be tedious.
Because the tetration function is neither commutative nor associative and has no identity element, we cannot apply (2) Use of the properties of binary operations.
Could we apply (3) Identifying extremal points? Let's find out.
Let \(x\) denote the value that represents the leftmost box as highlighted below (the base of the entire exponent).
\[ \large {\color{green}{\square} ^ {\square ^ {\square ^ \square}}}\]
If we let \(x=1\), then for any exponent power, the answer will always be 1.
But if we let \(x = 2,3\) or \(4\), then for any exponent power the expression will always be greater than \(1 \).
Thus, since we want to minimize the resultant number, \(x\) must be 1.Now because \(x\) raised to the power of any finite number gives 1, it doesn't matter how we arrange the remaining numbers \((2, 3, 4).\) Thus there are 6 solutions, namely
\[ {\boxed1 }^{{\boxed2}^{{\boxed3}^{\boxed4}}}, \quad {\boxed1 }^{{\boxed2}^{{\boxed4}^{\boxed3}}}, \quad {\boxed1 }^{{\boxed3}^{{\boxed2}^{\boxed4}}}, \quad {\boxed1 }^{{\boxed3}^{{\boxed4}^{\boxed2}}}, \quad {\boxed1 }^{{\boxed4}^{{\boxed2}^{\boxed3}}}, \quad{\boxed1 }^{{\boxed4}^{{\boxed3}^{\boxed2}}}. \]
Though there isn't an exact formula to determine where each extremal point is for each problem, one should always try to familiarize themselves with the properties of real numbers and how they grow larger. Let's try the following example that also requires us to find the extremal point(s):
\[ \LARGE \square^\square \ + \ \square^\square \ + \ \square^\square \]
Six numbers \(1,2,3,4,5,\) and \(6\) are to be filled in the square boxes above (without repetition). Of all \(6!=720\) possible arrangements, find the minimum value of the resultant number.
Details and Assumptions
- As an explicit example, if the six numbers are \(2,2,2,3,3,\) and \(3,\) then the minimum resultant number is \(2^3+2^3+2^3=24.\)
See Part 1 and Part 3.
Long Division
In this section we will be applying some properties of simple long division. If you are not familiar with that concept, please see the main article first, long division.
There are a couple of recurring techniques that pop up in filling in the blanks in long division. Though some of the techniques are more popular than others, it's always best to use the simplest method possible. Here's a list of some of the most notable techniques:
| Method | Brief Description |
| 1) Converting long division to equation | It is more familiar for readers to convert a long division into an equation. |
| 2) Elimination by range | Decide which numbers immediately give an absurd result. |
| 3) Linking | Link the relationship between two or more blanks. |
| 4) Divisibility check | If you are given numbers below the dividend, you know the divisor must divide it, so eliminate the ones that the divisor doesn't divide. |
| 5) Trial and error | Do this only after you think you have reduced as far as possible by the above methods. This will list all the combinations left, and try each of them until you get an answer. It is advised to perform this only as the last step/resort. |
Let's apply these techniques in the following example:

Find every possible sum of all missing digits that satisfy the long division above.
Let us first apply (1) Converting long division to equation:
Denote \(X\) as the quotient of the long division, and denote \(Y\) as the units digit of the dividend.

Then we have \(9X + 2 = 20 + Y \), where \(X\) and \(Y\) are non-negative single digit integers.
Upon simplifying, we get \( 9X = 18 + Y \).Since \(X\) is a single digit integer, \(9X\) is divisible by 9.
So we apply (4) Divisibility checking: \(18+ Y\) must be divisible by 9 as well.
Since \(0\leq Y\leq9 \), it follows that \(Y= 0\) or \(Y = 9\) only.If \(Y = 0 \), then \(9X = 20 + Y = 20 + 0 \Rightarrow X = 2 \).
If \(Y = 9 \), then \(9X = 20 + 7 = 27 \Rightarrow X = 3 \).
So we have two possible long divisions:

Now we can fill in the two boxes at the bottom: \(9\times2 = 18\) and \(9\times 3 = 27 \).

Therefore, the possible sums of all the missing numbers are \(2 + 0 + 1 + 8 = 11\) and \(3 + 9 + 2 + 7 = 21 \). \(_\square\)
Do you think that a larger long division makes the problem harder? Let's look at this slightly harder problem:
Complete the long division below, where each blank represents a single digit positive integer.

Let's start from the bottom because that's the only place where the integers are given.
We apply (1) Converting long division to equation: Between 13 and the two-digit integer above it, the difference is 3. So the two digit integer equals \(13 + 3= 16 ,\) implying the units digit of the 3-digit dividend must be 6.

Next, notice that for the boxes highlighted below in the long division on the left, we apply (3) Linking: we have \(\color{green}{ \square \, \square \times \square = \boxed{1} \, \boxed{3}} \). Since \(13\) is a prime number, the solution must be \(13 \times1 = 13 \) only. Thus we can fill in the respective boxes, as shown in the long division on the right.

Now what's left is to find the remaining 4 missing digits. Converting the relevant missing parts into an equation gives \( 13\times \, \square + 1= 50 + \square \). To avoid confusion, let's rewrite this in simpler terms: \(13X + 1 = 50 + Y, \) where \(X\) and \(Y\) are single digit non-negative integers. Upon simplifying, we get \(13X = 49 + Y \). By (4) Divisibility check, \(49 + Y\) must be divisible by 13, implying \(Y = 2 \) only and thus \(X = 4 \). Hence, we can complete the long division as follows:
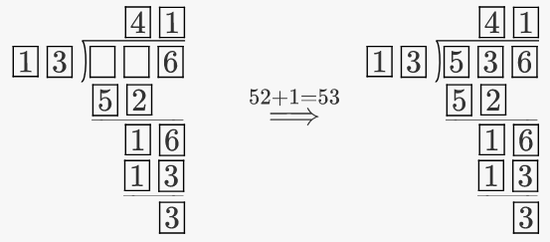
Did you notice that we didn't even use (5) Trial and error at all? That was because there wasn't a need for it. We should only apply it once we have exhausted all our efforts.
Now that you have learned how to solve long division arithmetic puzzles, try some made by our community!
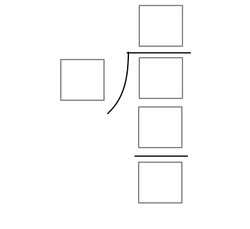 The above shows a long division between 2 integers, with the last box at the bottom representing the non-zero remainder of the quotient. Each box represents a distinct single digit positive integer.
The above shows a long division between 2 integers, with the last box at the bottom representing the non-zero remainder of the quotient. Each box represents a distinct single digit positive integer.
Of all the possible solutions, there is only 1 possible value for the remainder of this long division. What is it?
 The above shows a long division between 2 integers, with the last box at the bottom representing the remainder of the quotient. Each box represents a single digit non-negative integer.
The above shows a long division between 2 integers, with the last box at the bottom representing the remainder of the quotient. Each box represents a single digit non-negative integer.
What is the sum of all the missing numbers?

The above shows a long division, where the divisor is strictly greater than the remainder and the quotient is a single-digit number.
Is it possible to fill each box with a distinct, non-negative single digit?
Inspiration.