Basics of Statistical Mechanics

In most realistic situations, we can only predict the motion and future of a particle if

• we are given the initial conditions;
• we are given the present forces acting upon it and the particles with which it is interacting.

However, when it comes to objects like a box of gas which can be visualized classically as hard spheres going all about, we cannot know the initial conditions since it is too complicated and of course hard to measure. Moreover, if we observe a gas being made (say by vaporizing a solid), we cannot be sure or even get a vague idea of the initial velocity of each and every gas atom/molecule. In such scenarios, we face an uncertainty because of lack of information and hence we lose our ability to predict.

But even such situations can be analyzed if we assume the following reasonable assumption:

For an arbitrary system, the system will assume the state that is most likely to happen given enough time. (For example, toss a thousand coins and you will more or less end up with half heads and half tails.)

So now we have to explain what it means by a state and how to define which state is more likely than others.

We have two forms of state:

1. Microstate: Microstate is defined as the exact arrangement (distribution of velocities, etc.) of each and every individual particle.

   • Example 1: If we have a single particle in free space which has an energy of \(E,\) then it can have two velocities \(+V\) and \(-V.\) These two are the microstates of the system.
   • Example 2: If we have 10 coins in a row, each labeled with a number, then the series of individual states (say, HTTHHHTHHT) is a microstate. Each microstate is equally likely (evidently) assuming that each particle/coin is identical.

2. Macrostate: A macrostate is the set of microstates that correspond to a common quantity in the particle example above. The energy \(E\) can be said to be the macrostate for the microstates \(+V\) and \(-V.\) Similarly, 6 heads and 4 tails is a macrostate. However, each macrostate is not necessarily equally probable and, in fact, its probability is proportional to the number of microstates it possesses.

So, for a system of gas molecules, the energy it has is a macrostate and the number of ways it can distribute that energy amongst its particles is its microstate. Now with the definitions made clear, we need to quantize our ideas.

Consider the two systems joined to each other by a fixed conducting wall (energy can pass, material cannot). Let the total energy of the system be \(E,\) and the energy of each system \( E_1\) and \(E_2.\) Also, let \(\Omega _{ E_1 }\) and \(\Omega _{E_2 }\) be the number of microstates corresponding to each system with respective energies. Then, for each microstate of 1, we can have \(\Omega _{E_2 }\) microstates of 2 and hence the total number of microstates is \(\Omega_{ E_1 }\Omega_{ E_2 }.\)

As per our assumptions, this must be maximized to get the most probable distribution. So, differentiating with respect to \(E_1\) and equating to 0 gives

\[{ \Omega }_{ E_2 }\frac { d{ \Omega }_{ E_1 } }{ d{ E }_{ 1 } } +{ \Omega }_{ E_1 }\frac { d{ \Omega }_{ E_2 } }{ d{ E }_{ 1 } } =0.\]

Now we invoke conversation of energy to claim

\[ d{ E }_{ 1 }+d{ E }_{ 2 }=0\]

and substitute to get

\[\frac { 1 }{ { \Omega }_{ E_1 } } \frac { d { \Omega }_{ E_1 } }{ d{ E }_{ 1 } } =\frac { 1 }{ { \Omega }_{ E_2 } } \frac { d { \Omega }_{ E_2 } }{ d{ E }_{ 2 } },\]

which is equivalent to

\[ \frac { d\, { \ln\big(\Omega }_{ E_1 }\big) }{ d{ E }_{ 1 } } =\frac { d\, {\ln\big(\Omega }_{ E_2 }\big) }{ d{ E }_{ 2 } }. \]

Now, we have a very powerful relation, in general, for \(n\) systems in thermal equilibrium. The quantity that must remain invariant for all of them is

\[\frac { d\, { \ln\big(\Omega }_{ E }\big) }{ d{ E } }. \]

Let's call this quantity \(\frac { 1 }{ kT } \) (the reasons will soon be apparent). So for \(n\) systems in thermal equilibrium, \(T\) must be the same for all. Let's call this the temperature.

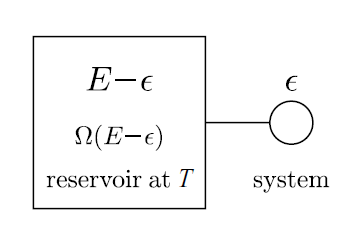
Now, we use the results of the previous section to prove very powerful and general result, using which we can deal with most statistical systems. Imagine a small tank connected to a large reservoir, as shown in the second figure. Once again let the total energy of the system be \(E.\) Since the reservoir is so large, most of the overall energy comes from the reservoir. So, let the energy of the small tank be \(\epsilon, \) and the energy of the reservoir \(E-\epsilon. \)

Now, we make a special assumption. Let the number of microstates for each macrostate of the small tank be fixed and equal to \(n.\) Then

\[P(\epsilon ) \propto n{ \Omega }_{ E-\epsilon },\]

where \(P\) is the probability of having that energy (it is proportional to the number of microstates). Now, as \(n\) is fixed, we can further write

\[P(\epsilon ) \propto { \Omega }_{ E-\epsilon }.\]

Taking \(\ln\) on both sides gives

\[\begin{align} \ln \big(P(\varepsilon )\big) \propto &\ln ({ \Omega }_{ E-\epsilon })\\ &\approx \ln({ \Omega }_{ E })-\epsilon \frac { d \ln({ \Omega }_{ E }) }{ d\epsilon } \\ &=\ln({ \Omega }_{ E })-\frac { \epsilon }{ kT }. \end{align} \]

So,

\[P(\epsilon ) = A{ e }^{ -\frac { \epsilon }{ kT } }.\]

The importance of this result cannot be overstressed despite the delicate assumption we have made about the fixed number of microstates. For example, let us imagine a particle in a 1D universe. For each energy \(E,\) it can have velocities \(+V\) and \(-V,\) so here the \(n\) value is 2.

The small tank need not be a tank. Any single molecule in a gas in steady state is interacting with several other molecules through collisions, thus gaining and losing energy. Here the gas molecule can be called as the small tank and the rest of the vast number of gas molecules as the reservoir. Thus, the probability of the gas molecule having energy \(\epsilon \) is proportional to \({ e }^{ -\frac { \epsilon }{ kT } }.\)

In future edits or in another wiki, we shall derive the Maxwell-Boltzmann distribution using this.