Benford's Law
Benford's law is an observation about the leading digits of the numbers found in real-world data sets. Intuitively, one might expect that the leading digits of these numbers would be uniformly distributed so that each of the digits from 1 to 9 is equally likely to appear. In fact, it is often the case that 1 occurs more frequently than 2, 2 more frequently than 3, and so on. This observation is a simplified version of Benford's law. More precisely, the law gives a prediction of the frequency of leading digits using base-10 logarithms that predicts specific frequencies which decrease as the digits increase from 1 to 9.
This phenomenon occurs generally in many different instances of real-world data. It becomes more pronounced and more likely when more data is combined together from different sources. Not every data set satisfies Benford's law, and it is surprisingly difficult to explain the law's occurrence in the data sets it does describe, but nevertheless it does occur consistently in well-understood circumstances. Scientists have even begun to use versions of the law to detect potential fraud in published data (tax returns, election results) that are expected to satisfy the law.
Here is a histogram of the areas of \( 196 \) countries (data taken from Wikipedia). The units are \( \text{km}^2 \).

Here is a table with percentages. The "BL prediction" column is the percentage that Benford's law predicts for each digit. (These numbers will be explained in the full statement of the law in the next section.)
First digit Number of countries Percentage BL prediction 1 56 29% 30% 2 37 19% 18% 3 23 12% 12% 4 22 11% 10% 5 11 6% 8% 6 16 8% 7% 7 12 6% 6% 8 8 4% 5% 9 11 6% 4%
Here is a histogram of the population of each of the 3,142 counties or county equivalents in the United States (data taken from Wikipedia).

Here is a table with percentages.
First digit Number of counties Percentage BL prediction 1 956 30% 30% 2 593 19% 18% 3 380 12% 12% 4 301 10% 10% 5 225 7% 8% 6 203 6% 7% 7 177 6% 6% 8 159 5% 5% 9 148 5% 4%
So Benford's law appears to predict the data in both examples quite well.
A set of \( 1000 \) numbers between \( 1 \) and \( 10^6-1 \) generated by a random number generator will produce a distribution that does not follow Benford's law. In fact, the first digits of these numbers should be evenly distributed between all nine possibilities. (Computer science exercise: write a program to generate such a set, and verify that the first digits of the results are roughly equally distributed.)
Contents
Statement of the Law
A set of numbers is said to satisfy Benford's law if the leading digit \( d \) \( (d \in {1, \ldots , 9}) \) occurs with probability
\[ P(d) = \log_{10}(d+1) - \log_{10}(d) = \log_{10}\bigg( \frac{d+1}{d} \bigg) = \log_{10}\bigg( 1 + \frac{1}{d} \bigg). \]
The leading digits in such a set thus have the following distribution:
\(d \hspace{10mm}\) \(P(d)\) 1 30.1% 2 17.6% 3 12.5% 4 9.7% 5 7.9% 6 6.7% 7 5.8% 8 5.1% 9 4.6%
Benford's law predicts a probability of \( \log_{10}\left(1+\dfrac1{d}\right) \) that a randomly chosen number in a given data set starts with the digit (or digits) \( d \). If these probabilities are close to the actual probabilities for a given data set, then that data set is sometimes said to be Benford, e.g. "areas of countries are Benford" or "populations of counties are Benford."
Notes:
(1) Note that \[ \begin{align} \sum_{d=1}^9 \log_{10}\left( 1 + \frac1{d}\right) &= \sum_{d=1}^9 \log_{10}\left(\frac{d+1}{d} \right) \\ &= \sum_{d=1}^9 \big(\log_{10}(d+1) - \log_{10}(d)\big) \\ &= \log_{10}(10)-\log_{10}(1) \\ &= 1 \end{align} \] because the series telescopes. So the probabilities in Benford's law do indeed sum to 1. \((\)The same argument works for all two-digit \( d\), or all \(k\)-digit \( d \) for a fixed \( k.) \)
(2) There is nothing special about decimal digits in this context. Benford's law applies in other bases as well; simply replace the \( 10 \) by the base \( b \) in the logarithms.
(3) Frank Benford, the namesake of the law, was a research physicist at General Electric. In a 1938 paper, he collected more than 20,000 numbers from 20 disparate sources and showed that these data sets all satisfied the law. (He was not actually the first to notice the law; the American astronomer Simon Newcomb pointed it out in 1881, after noticing that books of logarithm tables were much more worn and dog-eared at pages corresponding to numbers starting with 1 or 2.)
Invariance under Scaling
One way to understand the law is that it should be independent of units. For instance, the first example was of areas in \( \text{km}^2 \), but the data could equally well have been presented in square miles, or square feet, or acres, or any other measure of area (as the graph below shows, raw data available here). This would scale the data, multiplying it by a constant (the ratio of the two units).
 The distribution of the first digit of 197 countries, scaled to square miles, square feet, and acres
The distribution of the first digit of 197 countries, scaled to square miles, square feet, and acres
The probability distribution described by Benford's law behaves well under scaling.
If a data set is Benford, then the set obtained by multiplying all the numbers in the original set by a fixed constant will also be Benford.
Let \( d \) be a positive integer and \( c \) be the constant. For simplicity, take \( c= 2 \); the generalization to arbitrary \( c \) requires some work, but the general idea is clear from this case.
The probability that \( 2x\) starts with \( d \) is equal to the probability that \( x \) starts with the digits \( 5d, 5d+1, 5d+2, 5d+3,\) or \( 5d+4\). For example, if \( d= 13 \), then numbers that start with \( 65, 66, 67, 68, 69 \) will start with \( 13 \) when multiplied by \( 2 \). This probability is \[ \begin{align} \log_{10}\left(1+\frac1{5d}\right)+\log_{10} \left(1+\frac1{5d+1}\right)+\cdots+\log_{10}\left(1+\frac1{5d+4}\right) &= \log_{10}\left(\frac{5d+5}{5d}\right) \\ &= \log_{10}\left(1+\frac1{d}\right), \end{align} \] as desired. \(_\square\)
Under some assumptions, it can be shown that the Benford distribution is the only distribution that satisfies this scale-invariance requirement. So data sets consisting of widely distributed numbers with somewhat arbitrary units should be expected to be Benford.
Explanation of the Law
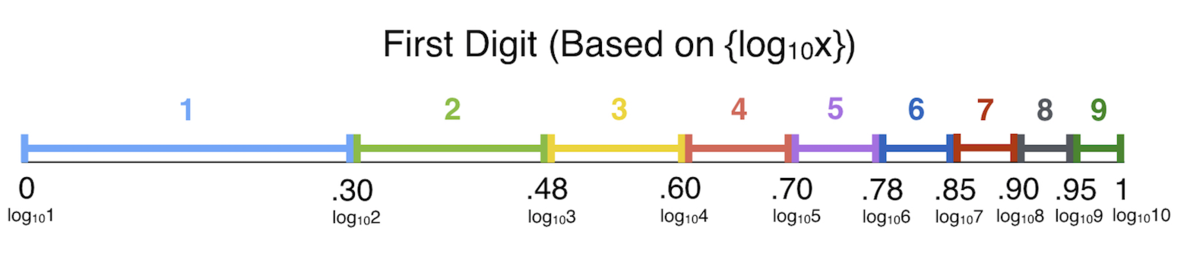
Perhaps the easiest way to explain Benford's law directly is to consider the (base-10) logarithms of the numbers in a given data set. If their fractional parts are uniformly (evenly) distributed inside the interval \( [0,1]\), then the data set will be Benford.
To see this, note that \( x \) starts with a digit \( d \) if and only if
\[ \log_{10}(d) \le \{\log_{10}(x)\} < \log_{10}(d+1),\]
i.e. \( \{\log_{10}(x)\} \) lies in an interval of length \( \log_{10}(d+1)-\log_{10}(d) = \log_{10}\left( 1+\frac1{d}\right)\).
For example, \(74923\) starts with a \(7\) because \(\{\log_{10}\left(74923\right)\} \approx \{4.87\} = 0.87\) lies between \(\log_{10}\left(7\right) \approx 0.85\) and \(\log_{10}\left(8\right) \approx 0.90.\) If the set of values of \( \{\log_{10}(x)\},\) for \( x \) in the data set, is uniformly distributed in \( [0,1]\), then the probability that this happens will just be the width of the interval, or \( \log_{10}\left(1+\frac1{d}\right), \) as Benford's law predicts.
Most sets of "naturally" occurring numbers should not have any bias in the fractional parts of their logarithms, so they will be Benford. Note that the third introductory example does have this bias: evenly-spaced positive integers will not have evenly-spaced logarithms. In fact, the fractional parts of the logarithms of these integers will be more likely to be close to \( 1 \) than to \( 0 \). \((\)For instance, consider the integers between \( 10 \) and \( 99 \), whose logarithms all have integer part equal to \( 1 \). Because \( \log(x)\) is concave down, there will be more integers whose logarithm is greater than \( 1.5 \) than those whose logarithm is less than \( 1.5.) \) This exactly offsets the Benford tendency to skew toward earlier digits.
Applications to Fraud Detection
It is difficult for humans to manually construct distributions that satisfy Benford's law. Fraudulent numerical data can often be identified by simply looking at the frequency of first digits, although often in practice more than one digit is used for a more precise check. In particular, Benford's law has been applied to entries on tax forms, election results, economic numbers, and accounting figures.