Bijection, Injection, And Surjection
Functions can be injections (one-to-one functions), surjections (onto functions) or bijections (both one-to-one and onto). Informally, an injection has each output mapped to by at most one input, a surjection includes the entire possible range in the output, and a bijection has both conditions be true.

This concept allows for comparisons between cardinalities of sets, in proofs comparing the sizes of both finite and infinite sets.
Definition of a Function
A function \(f \colon X\to Y\) is a rule that, for every element \( x\in X,\) associates an element \( f(x) \in Y.\) The element \( f(x)\) is sometimes called the image of \( x,\) and the subset of \( Y \) consisting of images of elements in \( X\) is called the image of \( f.\) That is,
\[\text{image}(f) = \{ y \in Y : y = f(x) \text{ for some } x \in X\}.\]
Injective
Let \(f \colon X \to Y\) be a function. Then \(f\) is injective if distinct elements of \(X\) are mapped to distinct elements of \(Y.\)
That is, if \(x_1\) and \(x_2\) are in \(X\) such that \(x_1 \ne x_2\), then \(f(x_1) \ne f(x_2)\).
This is equivalent to saying if \(f(x_1) = f(x_2)\), then \(x_1 = x_2\).
A synonym for "injective" is "one-to-one."
The function \( f\colon {\mathbb Z} \to {\mathbb Z}\) defined by \( f(n) = 2n\) is injective: if \( 2x_1=2x_2,\) dividing both sides by \( 2 \) yields \( x_1=x_2.\)
The function \( f\colon {\mathbb Z} \to {\mathbb Z}\) defined by \( f(n) = \big\lfloor \frac n2 \big\rfloor\) is not injective; for example, \(f(2) = f(3) = 1\) but \( 2 \ne 3.\)
The function \( f\colon \{ \text{German football players dressed for the 2014 World Cup final}\} \to {\mathbb N} \) defined by \(f(A) = \text{the jersey number of } A\) is injective; no two players were allowed to wear the same number.
The existence of an injective function gives information about the relative sizes of its domain and range:
If \( X \) and \( Y \) are finite sets and \( f\colon X\to Y \) is injective, then \( |X| \le |Y|.\)
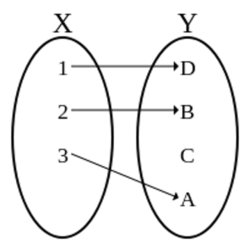
Let \(f\) be a one-to-one (Injective) function with domain \(D_{f} = \{x,y,z\} \) and range \(\{1,2,3\}.\) It is given that only one of the following \(3\) statement is true and the remaining statements are false:
\[ \begin{eqnarray} f(x) &=& 1 \\ f(y) & \neq & 1 \\ f(z)& \neq & 2. \\ \end{eqnarray} \]
Find \( f^{-1} (1). \)
Surjective
Let \(f \colon X\to Y\) be a function. Then \(f\) is surjective if every element of \(Y\) is the image of at least one element of \(X.\) That is, \( \text{image}(f) = Y.\)
Symbolically,
\[\forall y \in Y, \exists x \in X \text{ such that } f(x) = y.\]
A synonym for "surjective" is "onto."
The function \( f\colon {\mathbb Z} \to {\mathbb Z}\) defined by \( f(n) = 2n\) is not surjective: there is no integer \( n\) such that \( f(n)=3,\) because \( 2n=3\) has no solutions in \( \mathbb Z.\) So \( 3\) is not in the image of \( f.\)
The function \( f\colon {\mathbb Z} \to {\mathbb Z}\) defined by \( f(n) = \big\lfloor \frac n2 \big\rfloor\) is surjective. For any integer \( m,\) note that \( f(2m) = \big\lfloor \frac{2m}2 \big\rfloor = m,\) so \( m \) is in the image of \( f.\) So the image of \(f\) equals \(\mathbb Z.\)
The function \(f \colon \{\text{US senators}\} \to \{\text{US states}\}\) defined by \(f(A) = \text{the state that } A \text{ represents}\) is surjective; every state has at least one senator.
The existence of a surjective function gives information about the relative sizes of its domain and range:
If \( X \) and \( Y \) are finite sets and \( f\colon X\to Y \) is surjective, then \( |X| \ge |Y|.\)
Bijective
A function is bijective for two sets if every element of one set is paired with only one element of a second set, and each element of the second set is paired with only one element of the first set. This means that all elements are paired and paired once.
Let \(f \colon X \to Y \) be a function. Then \(f\) is bijective if it is injective and surjective; that is, every element \( y \in Y\) is the image of exactly one element \( x \in X.\)
The function \( f \colon {\mathbb R} \to {\mathbb R} \) defined by \( f(x) = 2x\) is a bijection.
The function \( f \colon {\mathbb Z} \to {\mathbb Z} \) defined by \( f(n) = \begin{cases} n+1 &\text{if } n \text{ is odd} \\ n-1&\text{if } n \text{ is even}\end{cases}\) is a bijection.
The function \( f\colon \{ \text{months of the year}\} \to \{1,2,3,4,5,6,7,8,9,10,11,12\} \) defined by \(f(M) = \text{ the number } n \text{ such that } M \text{ is the } n^\text{th} \text{ month}\) is a bijection.
Note that the above discussions imply the following fact (see the Bijective Functions wiki for examples):
If \( X \) and \( Y \) are finite sets and \( f\colon X\to Y \) is bijective, then \( |X| = |Y|.\)
The following alternate characterization of bijections is often useful in proofs:
Suppose \( X \) is nonempty. Then \( f \colon X \to Y \) is a bijection if and only if there is a function \( g\colon Y \to X \) such that \( g \circ f \) is the identity on \( X \) and \( f\circ g\) is the identity on \( Y;\) that is, \(g\big(f(x)\big)=x\) and \( f\big(g(y)\big)=y \) for all \(x\in X, y \in Y.\) When this happens, the function \( g \) is called the inverse function of \( f \) and is also a bijection.
Show that the function \( f\colon {\mathbb R} \to {\mathbb R} \) defined by \( f(x)=x^3\) is a bijection.
Rather than showing \(f\) is injective and surjective, it is easier to define \( g\colon {\mathbb R} \to {\mathbb R}\) by \(g(x) = x^{1/3} \) and to show that \( g\) is the inverse of \( f.\) This follows from the identities \( \big(x^3\big)^{1/3} = \big(x^{1/3}\big)^3 = x.\) \(\big(\)Followup question: the same proof does not work for \( f(x) = x^2.\) Why not?\(\big)\)