Binary-Coded Decimal Or BCD
Contents
Definition
BCD or binary-coded decimal is a special kind of representation of a decimal number in binary numbers. In binary-coded decimal each individual digit of a number is converted into a binary number, and then by combining them all, the BCD code is generated. But always remember that a binary-coded decimal is not a binary representation of a decimal number.
Examples
The BCD or binary-coded decimal of the number 15 is 00010101. The 0001 is the binary code of 1 and 0101 is the binary code of 5.
Any single decimal numeral [0-9] can be represented by a four bit pattern. The procedure of encoding digits is called "Natural BCD" (NBCD), where each decimal digit is represented by its corresponding four-bit binary value.
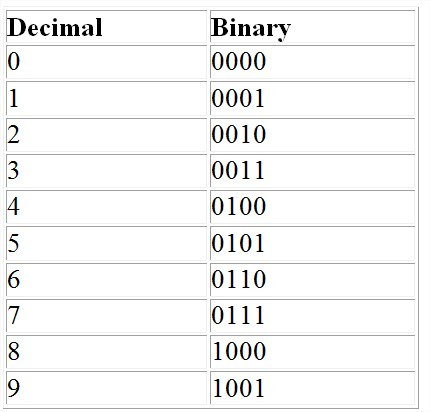
Types
Generally there are 2 types of BCD: unpacked and packed.
Unpacked BCD: In the case of unpacked BCD numbers, each four-bit BCD group corresponding to a decimal digit is stored in a separate register inside the machine. In such a case, if the registers are eight bits or wider, the register space is wasted.
Packed BCD: In the case of packed BCD numbers, two BCD digits are stored in a single eight-bit register. The process of combining two BCD digits so that they are stored in one eight-bit register involves shifting the number in the upper register to the left 4 times and then adding the numbers in the upper and lower registers.
There is the another one which is not really considered as BCD:
Invalid BCD: There are some numbers are not considered as BCD. They are 1010, 1011, 1100, 1101, 1110, 1111.
Differences Between BCD And Simple Binary Representation
In simple binary representation of any number we just convert the whole number into its binary form by repeteadly dividing 2 again and again. But in the case of BCD, we need not to do this. If anyone knows the binary representation of the numbers 0 to 9, he/she can make a BCD code of any number because, in BCD, we just convert each individual digit of any number to binary and then write them together.
In the case of 946, the binary representation of this number is 01110110010. Here we convert the total number into its binary form. But when we form the BCD code of the number 946, that'll be
\[9 = 1001, 4 = 0100, 6 = 0110 \Rightarrow 100101000110. \]
Use Of Binary-Coded Decimal
The use of BCD can be summarized as follows:
- BCD takes more space and more time than standard binary arithmetic.
- It is used extensively in applications that deal with currency because floating point representations are inherently inexact.
- Database management systems offer a variety of numeric storage options; “Decimal” means that numbers are stored internally either as BCD or as fixed-point integers
- BCD offers a relatively easy way to get around size limitations on integer arithmetic.
How many bits would be required to encode decimal numbers 0 to 9999 in straight binary and BCD codes? What would be the BCD equivalent of decimal 27 in 16-bit representation?
- Total number of decimals to be represented=10 000=104 = 213 29.
- Therefore, the number of bits required for straight binary encoding = 14.
- The number of bits required for BCD encoding = 16.
- The BCD equivalent of 27 in 16-bit representation = 0000000000100111.
Find a decimal number which can be represented with 1's only and no 0's in binary, and takes 4 bits in binary. In other words, if you convert that decimal number into binary, it cannot be like 10101 which does contain 0's. It should only contain a certain number of 1's.
Submit your answer as the sum of digits of the binary-coded decimal of that decimal number.
For binary-coded decimal, read the wiki Binary-Coded Decimal.