Do local extrema occur if and only if f'(x) = 0?
This is part of a series on common misconceptions.
True or False?
Local extrema of \(f(x)\) occur if and only if \(f'(x) = 0.\)
Why some people say it's true: That is the first derivative test we were taught in high school.
Why some people say it's false: There are cases that are exceptions to this statement. Also, I was taught that this is just the first step of the first derivative test.
The statement is \( \color{red}{\textbf{false}}\).
Knowing that a function's derivative is 0 at a specific point does not necessarily mean that there's a local minimum or maximum at that point. When \(f'(x) = 0,\) it only implies that there is a horizontal tangent at that point. An example of the case when a function has a horizontal tangent at a point that is not a local extremum is given below.
Additionally, it's possible for a function to have a local minimum or maximum at a point where its derivative is non-zero in a variety of different ways outlined further below. For example, \(f(x) = |x|\) has a local minimum at \(x = 0,\) despite \(f'(0) \neq 0.\)
Counterexample 1:
This is a simple counterexample of the given statement: an example of when the derivative of a function is 0 at a point which is not a local extremum.
Consider the example of \(f(x) =x^3\), which is continuous and differentiable everywhere \((\)for all \(x \in \mathbb{R}).\)
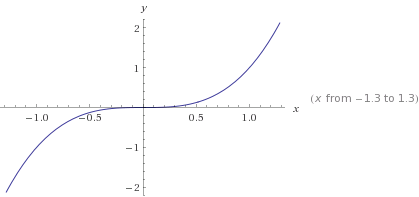
Differentiating \(f(x)\) with respect to \(x,\) we have \(f'(x) = 3x^2 .\) Setting it to zero, we get \(x = 0.\) But graphically we can clearly see that the function does not attain a local extremum at \(x = 0.\) The curve merely goes from being concave downwards for \(x < 0\) to being concave upwards for \(x > 0.\) \(_\square\)
\[\]
Counterexample 2:
\(y = \sin x\) for \( 0 ≤ x ≤ \frac{\pi}{3}\) is an example of a function which has a local extremum at a point where its derivative is not 0. This occurs because the function has a restricted domain.
Shown below is the graph of \(y = \sin x\) for \( 0 ≤ x ≤ \frac{\pi}{3}.\)

The function attains its maximum value at \( x = \frac{\pi}{3} \) and minimum at \(x = 0:\)
\[\begin{array} &f_{\text{max}}(x)=\sin \dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}, &f_{\text{min}}(x) = \sin 0 = 0.\end{array} \]
However, the derivative of the function \(f'(x) = \cos x\) is not equal to zero at any of the points:
\[\begin{array} &f '(0) =\cos 0 = 1, &f'\left(\dfrac{\pi}{3}\right) =\cos \dfrac{\pi}{3} = \dfrac{1}{2},\end{array} \]
implying the given statement is false. \(_\square\)
More information on local and global extrema can be found here: Extrema.
The following are two common objections to the counterexample given above:The local extrema of \(y = \sin x\) for \( 0 ≤ x ≤ \frac{\pi}{3}\) are
\[\begin{array} &f_{\text{max}}(x)=\sin \dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}, &f_{\text{min}}(x) = \sin 0 = 0.\end{array} \]
Rebuttal: The gradient of the function is positive at \(x = \frac{\pi}{3}\), and therefore it is increasing and the value we got isn't the local maximum.
Reply: The function isn't defined for \(x > \frac{\pi}{3} \) , and hence we have indeed reached the local maximum at \( x = \frac{\pi}{3} .\)
Rebuttal: Isn't \(-1\) the minimum value of \(\sin x?\)
Reply: The minimum value of the function \(\sin x\) in the domain \( 0 ≤ x ≤ \frac{\pi}{3} \) is not \(-1.\) The value \(-1\) corresponds to the minimum value on a larger domain.

The graph at right depicts the function \(\color{darkred}{f(x)} = |\cos x + 0.5|\) in the interval \(\color{darkred}0 \leq \color{darkred}x \leq \color{darkred}{10} \).
How many local extrema does the function \(f(x) \) have if its domain is restricted to \({\color{darkred}0 \leq \color{darkred}x \leq \color{darkred}{10}}?\)
See Also