Extrema (Local and Absolute)
An extremum (or extreme value) of a function is a point at which a maximum or minimum value of the function is obtained in some interval. A local extremum (or relative extremum) of a function is the point at which a maximum or minimum value of the function in some open interval containing the point is obtained.
An absolute extremum (or global extremum) of a function in a given interval is the point at which a maximum or minimum value of the function is obtained. Frequently, the interval given is the function's domain, and the absolute extremum is the point corresponding to the maximum or minimum value of the entire function.
 This function has an absolute extrema at \(x = 2\) and a local extrema at \(x = -1\). What other extrema does it have?
This function has an absolute extrema at \(x = 2\) and a local extrema at \(x = -1\). What other extrema does it have?
Extrema (maximum and minimum values) are important because they provide a lot of information about a function and aid in answering questions of optimality. Calculus provides a variety of tools to help quickly determine the location and nature of extrema.
Global Extrema
A point \(x\) is an absolute maximum or minimum of a function \(f\) in the interval \([a, \, b]\) if \(f(x) \ge f(x')\) for all \(x' \in [a, \, b]\) or if \(f(x) \le f(x')\) for all \(x' \in [a, \, b]\). The point \(x\) is the strict (or unique) absolute maximum or minimum if it is the only point satisfying such constraints. Analogous definitions hold for intervals \([a, \, \infty)\), \((-\infty, \, b]\), and \((-\infty, \, \infty)\). The interval is commonly chosen to be the domain of \(f\).
 The absolute maximum and absolute minimum of the function
The absolute maximum and absolute minimum of the function
There may not exist an absolute maximum or minimum if the region is unbounded in either the positive or negative direction or if the function is not continuous. If the function is not continuous (but is bounded), there will still exist a supremum or infimum, but there may not necessarily exist absolute extrema. If the function is continuous and bounded and the interval is closed, then there must exist an absolute maximum and an absolute minimum.
If a function is not continuous, then it may have absolute extrema at any points of discontinuity. Generally, absolute extrema will only be useful for functions with at most a finite number of points of discontinuity. The absolute extrema can be found by considering these points together with the following method for continuous portions of the function.
If a function is continuous, then absolute extrema may be determined according to the following method. Given a function \(f\) and interval \([a, \, b]\),
- Determine all critical points of \(f\) in the interval \([a, \, b]\).
- Determine the value of \(f\) at each of its critical points.
- Determine the value of \(f\) at each of the endpoints.
The point(s) corresponding to the largest values of \(f\) are the absolute maximum (maxima), and the point(s) corresponding to the smallest values of \(f\) are the absolute minimum (minima). The other values may be local extrema.
Determine the absolute maxima and minima of the following function in the interval \(\left[-\tfrac{3}{2}, \tfrac{7}{2}\right]:\)
\[f(x) = \begin{cases} 1 - (x+1)^2 &\ x < 0 \\ 2x &\ 0 \le x \le 1 \\ 3 - (x - 2)^2 &\ 1 < x \le 2 \\ 3 - (x - 2)^3 &\ x > 2. \end{cases}\]

The function has critical points at \(x = -1\), \(x = 0\), \(x = 1\), and \(x = 2\). It has endpoints at \(x = -\tfrac{3}{2}\) and \(x = \tfrac{7}{2}\).
The only possibilities for the maximal value are \(x = -1\), \(x = 1\), and \(x = 2\). Since \(f(-1) = 1\), \(f(1) = 2\), and \(f(2) = 3\), the absolute maxima is located at \(\boxed{(2, \, 3)}\).
The only possibilities for the minimal value are \(x = -\tfrac{3}{2}\), \(x = 0\), \(x = 1\), and \(x = \tfrac{7}{2}\). Since \(f\left(-\tfrac{3}{2}\right) = \tfrac{3}{4}\), \(f(0) = 0\), \(f(1) = 2\), and \(f\left(\tfrac{7}{2}\right) = -\tfrac{3}{8}\), the absolute minima is located at \(\boxed{\left(\tfrac{7}{2}, -\tfrac{3}{8}\right)}\). \(_\square\)
Local Extrema
 The local maxima of the function
The local maxima of the function
 The local minima of the function
The local minima of the function
A point \(x\) is a local maximum or minimum of a function if it is the absolute maximum or minimum value of a function in the interval \((x - c, \, x + c)\) for some sufficiently small value \(c\).
Many local extrema may be found when identifying the absolute maximum or minimum of a function.
Given a function \(f\) and interval \([a, \, b]\), the local extrema may be points of discontinuity, points of non-differentiability, or points at which the derivative has value \(0\). However, none of these points are necessarily local extrema, so the local behavior of the function must be examined for each point. That is, given a point \(x\), values of the function in the interval \((x - c, \, x + c)\) must be tested for sufficiently small \(c\).
| Before (\( a < x \)) | After (\( a > x \)) | Extremum? |
| \(f(a) < f(x)\) | \(f(a) > f(x)\) | No |
| \(f(a) < f(x)\) | \(f(a) < f(x)\) | Maximum |
| \(f(a) > f(x)\) | \(f(a) < f(x)\) | No |
| \(f(a) > f(x)\) | \(f(a) > f(x)\) | Minimum |
If the function is twice differentiable at \(x\), then there is a somewhat simpler method available.
| \(f''(x)\) | Extremum? |
| Positive | Minimum |
| Negative | Maximum |
| Zero | No |
Classify the local maxima and minima of the following function in the interval \(\left[-\tfrac{3}{2}, \tfrac{7}{2}\right]:\)
\[f(x) = \begin{cases} 1 - (x+1)^2 &\ x < 0 \\ 2x &\ 0 \le x \le 1 \\ 3 - (x - 2)^2 &\ 1 < x \le 2 \\ 3 - (x - 2)^3 &\ x > 2. \end{cases}\]

From the graph, it seems that the function increases before \(x = -1\), decreases between \(x = -1\) and \(x = 0\), increases from \(x = 0\) to \(x = 2\), and decreases after \(x = 2\). The local maxima are located at \(x = -1\) and \(x = 2\). The local minima is located at \(x = 0\) and the endpoint at \( x = \frac{7}{2} .\) \(_\square\)
What is the sum of all local extrema of the function \(f(x)=\lvert x \rvert?\)
Observe that \(f(x)=-x\) for \(x<0,\) \(f(x)=0\) for \(x=0,\) and \(f(x)=x\) for \(x>0.\) Then \(f'(x)=-1<0\) for \(x<0\) and \(f'(x)=1>0\) for \(x>0,\) which implies that the function decreases before \(x = 0\) and increases after \(x = 0\). So \(f(x)\) has a local minimum at \(x=0.\) Since the value of that local minimum is \(f(0)=0,\) the sum of all the local extrema is \(0.\) \( _\square \)
What is the range of possible values of the real number \(k\) such that the function
\[f(x)=x^3-2kx^2-4kx-11\]
has no extrema?
Differentiating \(f(x)\) with respect to \(x\) gives \(f'(x)=3x^2-4kx-4k.\) For the function \(f(x)\) to have no extrema, it must be true that the equation \(f'(x)=0\) has either a repeated root or non-real, complex roots. This is equivalent to saying that the discriminant of the equation \(f'(x)=3x^2-4kx-4k=0\) must be non-positive:
\[\frac{D}{4}=(-2k)^2-3\cdot(-4K)=4k(k+3)\le 0.\]
Therefore, the range of \(k\) such that \(f(x)\) has no extrema is
\[-3\le k \le 0. \ _\square\]

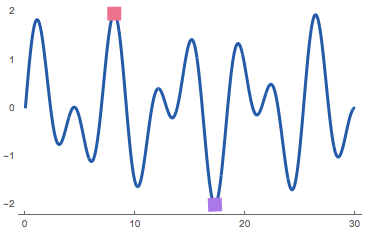
The graph at right depicts the function \(\color{darkred}{f(x)} = |\cos x + 0.5|\) in the interval \(\color{darkred}0 \leq \color{darkred}x \leq \color{darkred}{10} \).
How many local extrema does the function \(f(x) \) have if its domain is restricted to \({\color{darkred}0 \leq \color{darkred}x \leq \color{darkred}{10}}?\)
Differentiable Functions
Suppose the function in question is continuous and differentiable in the interval. Then, there are a few shortcuts to determining extrema. All local extrema are points at which the derivative is zero (though it is possible for the derivative to be zero and for the point not to be a local extrema). While they can still be endpoints (depending upon the interval in question), the absolute extrema may be determined with a few shortcuts, too. These are the derivative tests.
The First Derivative Test
Suppose \(f\) is a real-valued function and \([a, \, b]\) is an interval on which \(f\) is defined and differentiable. Then, if \(c\) is a critical point of \(f\) in \([a, \, b]\),
- if \(f'(x) > 0\) for all \(x < c\) and \(f'(x) < 0\) for all \(x > c\), then \(f(c)\) is the maximum value of \(f\) in the interval \([a, \, b];\)
- if \(f'(x) < 0\) for all \(x < c\) and \(f'(x) > 0\) for all \(x > c\), then \(f(c)\) is the minimum value of \(f\) in the interval \([a, \, b].\)
In simpler terms, a point is a maximum of a function if the function increases before and decreases after it. Conversely, a point is a minimum if the function decreases before and increases after it.
The Second Derivative Test
Suppose \(f\) is a real-valued function and \([a, \, b]\) is an interval on which \(f\) is defined and twice-differentiable. Then, if \(c\) is a critical point of \(f\) in \([a, \, b]\),
- if \(f''(x) < 0\) for all \(x\) in \([a, \, b]\), then \(f(c)\) is the maximum value of \(f\) in the interval \([a, \, b];\)
- if \(f''(x) > 0\) for all \(x\) in \([a, \, b]\), then \(f(c)\) is the minimum value of \(f\) in the interval \([a, \, b].\)
In simpler terms, a point is a maximum of a function if the function is concave down, and a point is a minimum of a function if the function is concave up.
The derivative tests may be applied to local extrema as well, given a sufficiently small interval. In fact, the second derivative test itself is sufficient to determine whether a potential local extremum (for a differentiable function) is a maximum, a minimum, or neither.
What is the sum of all the local extrema of the function \(f(x)=2x^3-6x-3?\)
Differentiating \(f(x)\) with respect to \(x\) gives \(f'(x)=6x^2-6=6(x+1)(x-1).\) Let \(f'(x)=0,\) then \(x=-1,\) or \(x=1.\) Then checking the sign of \(f'(x)\) around \(x=-1\) and \(x=1\) tells us that \(f'(x)>0\) for \(x<-1,\) \(f'(x)<0\) for \(-1<x<1,\) and \(f'(x)>0\) for \(x>1.\) This implies that \(f(x)\) has a local maximum at \(x=-1\) and a local minimum at \(x=1.\)
The value of the local maximum is \(f(-1)=2\cdot (-1)^3-6\cdot(-1)-3=1.\) The value of the local minimum is \(f(1)=2\cdot (1)^3-6\cdot(1)-3=-7.\) Thus, the sum of all the local extrema is \(1-7=-6.\) \( _\square \)
How many local extrema does the function \(f(x)=(x-1)^3+5\) have?
Differentiating \(f(x)\) with respect to \(x\) gives \(f'(x)=3(x-1)^2.\) Let \(f'(x)=0,\) then \(x=1.\) Then checking the sign of \(f'(x)\) around \(x=1\) tells us that \(f'(x)>0\) for \(x<1\) and \(f'(x)>0\) for \(x>1.\) This implies that \(f(x)\) has no local extrema with the slope of the function never switching signs.
Therefore, the number of local extrema is 0. \( _\square \)