Catalan Numbers

The Catalan numbers are a sequence of positive integers that appear in many counting problems in combinatorics. They count certain types of lattice paths, permutations, binary trees, and many other combinatorial objects. They satisfy a fundamental recurrence relation, and have a closed-form formula in terms of binomial coefficients.

The Catalan numbers $C_0,C_1, \ldots, C_n,\ldots$ are given by the formula

\[ C_n = \frac{1}{n+1}\dbinom{2n}{n}. \]

The first few Catalan numbers are

\[\begin{align} C_0 &= 1\\ C_1 &= 1\\ C_2 &= 2\\ C_3 &= 5\\ C_4 &= 14\\ C_5 &= 42. \end{align}\]

It is not immediately clear from the definition that the $ C_n $ are integers, but this will follow from many of the theorems proved below.

Dyck Paths and Acceptable Sequences

The number of valid parenthesis expressions that consist of $n$ right parentheses and $n$ left parentheses is equal to the $n^\text{th}$ Catalan number. For example, $C_3 = 5$ and there are 5 ways to create valid expressions with 3 sets of parenthesis:

( ) ( ) ( )

( ( ) ) ( )

( ) ( ( ) )

( ( ( ) ) )

( ( ) ( ) )

Considering right parenthesis to be +1s, and left -1s, we can write this more formally as follows:

The number of sequences $a_1,a_2, \ldots, a_{2n}$ of $2n$ terms that can be formed by using $n$ copies of $+1$'s and $n$ copies $-1$'s whose partial sums satisfy

\[a_1+a_2+\cdots+a_k \ge 0\]

for $k=1,2,3, \ldots, 2n$ equals the $n^\text{th}$ Catalan number.

Let us call a sequence of $n$ copies of $+1$'s and $n$ copies of $-1$'s to be acceptable if it satisfies the above condition, and unacceptable otherwise. We denote the number of acceptable sequences by $A_n$ and the number of unacceptable sequences by $U_n$.

The total number of sequences of $+1$'s and $-1$'s can be regarded as a permutation of objects with two different types with $n$ different objects of one type and $n$ of the other. So the total number of such sequences is

\[\dbinom{2n}{n} = \frac {2n!}{n!n!}.\]

So $ A_n =\dbinom{2n}{n} - U_n,$ and the next step is to count $ U_n$.

Consider an unacceptable sequence of $n$ copies of $+1$'s and $n$ copies of $-1$'s. Then there is a smallest $k$ for which the partial sum $a_1+a_2+\cdots+a_k$ is negative. By minimality of $ k,$ there must be an equal number of $+1$'s and $-1$'s preceding $a_k.$ So we must have $ k $ odd, $a_1+a_2+\cdots+a_{k-1} = 0,$ and $a_k = -1$. So among the terms $(a_1,a_2,...,a_k)$ there are $\frac{k-1}{2}$ copies of $+1$'s and $\frac{k-1}{2}+1=\frac{k+1}{2} $ copies of $-1$'s. Among the remaining terms $a_{k+1},....,a_{2n},$ there are $\big(n - \frac{k-1}{2}\big)$ copies of $+1$'s and $\big(n - \frac{k+1}{2}\big)$ copies of $-1$'s.

Now consider the effect of reversing the sign of each of the first $k$ terms, that is, replacing $a_i$ with $-a_i$ for $i= 1,2, \ldots, k$ and leaving the rest unchanged. Now this new sequence obtained, say $b_1,b_2,b_3, \ldots, b_{2n},$ will have $n+1$ copies of $ +1 $'s and $n-1$ copies of $ -1 $'s (since they add up to 2).

This gives a function $ f $ from the set of unacceptable sequences to the set of sequences of $ \pm 1 $ terms that add up to $ 2 $. To see that $ f$ is a bijection, construct its inverse: let $ B = b_1, b_2,\ldots, b_{2n} $ be a sequence of $ \pm 1 $ terms that add up to $ 2 $. Let $ k $ be the first index for which there are more $ +1$'s in $ b_1,\ldots,b_k $ than $ -1$'s. (There must be such a $ k $ since the sum of all the terms is positive.) Then define $ g(B) $ to be the (unacceptable) sequence $ -b_1, -b_2, \ldots, -b_k, b_{k+1}, b_{k+2}, \ldots, b_{2n} $. It is clear that $ f $ and $ g $ are inverses.

Now the number of sequences of $n+1$ copies of $+1$'s and $n-1$ copies of $-1$'s is $\frac{2n!}{(n+1)!(n-1)!}$. By the bijection, this is also equal to the number of unacceptable sequences. So the total number of unacceptable sequences is

\[U_n = \frac{2n!}{(n+1)!(n-1)!}.\]

So the number of acceptable sequences is

\[\begin{align} A_n &= \frac{(2n)!}{n!n!} - U_n\\ &= \frac{(2n)!}{n!n!} - \frac{(2n)!}{(n+1)!(n-1)!}\\ &= \frac{(2n)!}{n!(n-1)!} \left( \frac1{n}- \frac1{n+1}\right) \\ &= \frac{(2n)!}{n!(n-1)!} \frac1{n(n+1)} \\ &= \frac1{n+1} \frac{(2n)!}{n!n!} \\\\ &= C_n. \end{align}\]

This completes the proof. $_\square$

Notes:

(1) These sequences also describe Dyck paths of length $ 2n$, which are sequences of equally-spaced northeast and southeast walks starting at the origin, ending on the $x$-axis, and never going below the $x$-axis. The bijection between acceptable sequences and Dyck paths assigns a $+1$ to a northeast walk and a $ -1$ to a southeast walk, and the acceptability condition is equivalent to the path never dropping below the starting and finishing line.

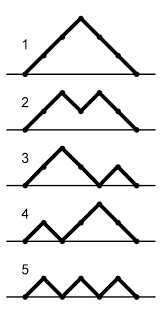$The five Dyck paths for $n=3.$$ The five Dyck paths for $n=3.$

(2) This shows that the Catalan numbers are integers, although this also follows from the identity $ C_n = \binom{2n}{n} - \binom{2n}{n+1} $ which comes up in the above proof.

Recurrence Relation; Generating Function

A useful tool in proofs involving the Catalan numbers is the recurrence relation that describes them.

The Catalan numbers satisfy the recurrence relation

\[ C_{n+1} = C_0 C_n + C_1 C_{n-1} + \cdots + C_n C_0 = \sum_{k=0}^n C_k C_{n-k}. \]

There are several ways to prove this, but perhaps the most elegant is by appealing to Dyck paths of length $ 2(n+1) $, which we saw above that $ C_{n+1} $ counts. Given a Dyck path of length $ 2(n+1), $ let $ 2(k+1) $ be the first nonzero $x$-coordinate where the path hits the $ x$-axis, then $ 0 \le k \le n $.

The path breaks up into two pieces, the part to the left of $ 2(k+1) $ and the part to its right. The part to the right is a Dyck path of length $ 2(n-k) $, so it is counted by $ C_{n-k} $. The part to the left is a northeast step, then a Dyck path of length $ 2k $, and then a southeast step. $\big($The middle path is a Dyck path "on stilts"; it never dips below its starting point because it cannot hit the $ x$-axis earlier than $ 2(k+1).\big) $ There are $ C_k $ of these. So there are a total of $ C_k C_{n-k} $ paths which hit the $ x$-axis first at $ 2(k+1) $, and summing these terms up gives $ C_{n+1} $, which is the recurrence relation. $_\square $

If $ n+1=3 $, then $ C_{n+1} $ counts the five Dyck paths pictured above:

Path 1 has $ k = 2 $, counted in $ C_2C_0 $.

Path 2 has $ k = 2 $, counted in $ C_2C_0 $.

Path 3 has $ k = 1 $, counted in $ C_1C_1 $.

Path 4 has $ k = 0 $, counted in $ C_0C_2 $.

Path 5 has $ k = 0 $, counted in $ C_0C_2 $.

The middle path of length $ 4 $ in paths 1 and 2, and the top half of the left peak of path 3, are the Dyck paths on stilts referred to in the proof above.

This recurrence is useful because it can be used to prove that a sequence of numbers is the Catalan numbers. If the sequence $($call it $S_n)$ satisfies the same recurrence as the Catalan numbers, and has the same initial condition $S_0 = 1,$ then $S_n=C_n$ by induction.

The generating function for the Catalan numbers is

\[\sum_{n=0}^\infty C_n x^n = \frac{1-\sqrt{1-4x}}{2x} = \frac2{1+\sqrt{1-4x}}.\]

Let $ f(x) = \sum\limits_{n=0}^\infty C_n x^n $. Then

\[\begin{align} xf(x)^2 &= \sum_{n=0}^\infty (C_0C_n + C_1 C_{n-1} + \cdots + C_nC_0) x^{n+1} \\ &= \sum_{n=0}^\infty C_{n+1}x^{n+1} \\ &= f(x)-1. \end{align}\]

So by the quadratic formula, $ f(x) = \frac{1\pm \sqrt{1-4x}}{2x} $, but the minus sign is the only choice that makes sense, because the plus sign leads to an expression that blows up at $ x = 0 $. $\Big($Choosing the minus sign leads to an expression that has a limit as $x\to 0$ by L'Hopital's rule: $\lim_{x\to 0} \frac{1-\sqrt{1-4x}}{2x} = \lim_{x \to 0} \frac{2(1-4x)^{-1/2}}2 = 1.\Big)\ _\square$

(Exercise: prove the theorem instead by using the binomial theorem on the right side.)

Other Appearances of the Catalan Numbers

Restricted random walks:

A man walks $n$ blocks north and $n$ blocks west of his residence. Every day he has $2n$ blocks to walk. How many routes are possible if he never crosses the diagonal line from home to office?

Clearly, each acceptable route is either above the diagonal or below the diagonal and both of these paths are symmetric. So we calculate the number of paths below the diagonal and multiply it by 2. Each route is a sequence of $n$ northerly blocks and $n$ westerly blocks. We identify west with $+1$ and north with $-1$. Each route corresponds to a sequence $a_1,a_2, \ldots, a_{2n}$ of $n$ copies of $+1$'s and $n$ copies of $-1$'s. But in order for the route not to go above the diagonal, we must have

\[a_1+a_2+\cdots+a_k \ge 0\]

for $k=1,2, \ldots, 2n$. So the number of acceptable routes above the diagonal equals the $n^\text{th}$ Catalan number, and the total number of acceptable routes is

\[2C_n = \frac{2}{(n+1)} \times \frac{(2n)!}{n!n!}.\]

The above diagram shows the routes below the diagonal for $n=5$. Notice that the number of such routes is equal to $C_5 = 42$. So the answer is $2\times 42=84.\ _\square$

Binary trees:

A rooted binary tree is a tree with one root node, where each node has either zero or two branches descending from it. A node is internal if it has two nodes coming from it. How many rooted binary trees are there with $n$ internal nodes? $Rooted binary trees with $0,1,2,3$ internal nodes.$ Rooted binary trees with $0,1,2,3$ internal nodes.^[1]

This is a good illustration of proving that a sequence equals the Catalan numbers by using the recurrence relation. Let $R_n$ be the number of rooted binary trees with $n$ internal nodes. Then $R_0=R_1 = 1$ as in the picture. Now for $n \ge 0,$ suppose there is a rooted binary tree with $n+1$ internal nodes. The root node is internal. There are $k$ internal nodes on the left and $n-k$ internal nodes on the right, for some $k.$ Looking at the left and right sides gives two rooted binary trees with $k$ and $n-k$ internal nodes, respectively. So

\[R_{n+1} = \sum_{k=0}^n R_kR_{n-k},\]

which is the same recurrence relation as the Catalan numbers. So $R_n = C_n$ for all $n.$ $_\square$

Polygon triangulations:

How many ways are there to cut an $ (n+2)$-gon into $ n $ triangles, by drawing $ n-1 $ non-crossing lines between vertices of the polygon?

$All the triangulations for $ n = 4 $$ All the triangulations for $ n = 4 $^[2]

Let $ T_n $ be the number of such triangulations, and define $ T_0 = 1 $. Consider $ T_{n+1} $, which counts triangulations of an $ (n+3)$-gon. The idea is to pick an edge of that $ (n+3)$-gon and classify triangulations by which triangle that edge ends up in.

Number the vertices $ v_1, v_2, \ldots, v_{n+3} $. Suppose our edge is $ v_1v_2 $. If the triangle this edge ends up in is $ v_1v_2v_k $, then this triangle splits the polygon into two remaining polygons that must be triangulated.

If $ k = 3 $, then what is left is an $ (n+2)$-gon. The number of triangulations like this is $ T_0 T_n $.

If $ k=4 $, there is a triangle $ v_2v_3v_4 $ on one side and an $ (n+1)$-gon on the other side. The number of triangulations like this is $ T_1 T_{n-1} $.

If $ k = 5 $, there is a quadrilateral $ v_2v_3v_4v_5 $ on one side and an $n$-gon on the other side. The number of triangulations like this is $ T_2 T_{n-2} $.

Proceeding in this way,

\[T_{n+1} = T_0T_n + T_1T_{n-1} + \cdots + T_n T_0.\]

Also $ T_0 = 1 $. This is the same recurrence relation and initial condition that the Catalan numbers satisfy, so it must be the case that $ T_n = C_n $ for all $ n $. $_\square$

For more examples, see the wiki on proofs using bijections.

References

Berkeley Math Circle, . Binary Tree. Retrieved September 9, 2014, from https://commons.wikimedia.org/wiki/File:Binary_Tree.png
Harvey, D. Catalan Hexagons. Retrieved April 8, 2009, from https://commons.wikimedia.org/wiki/File:Catalan-Hexagons-example.svg

Contents