Conductors
With electrostatics, the primary object of concern is static electric charges. But what if those charges are free to move? Very simply put, an ideal conductor is any material whose free electrons can move without any resistance. Of course, there are no perfect conductors, but many metals come amazingly close.
Even though our interest lies mostly in understanding the equilibrium (static) configuration of conductors, in some ways conductors represent one of the first examples of charges in flux. Using the laws of electrostatics, we can determine, for instance, the behavior of metal objects following perturbation, such as the introduction of an external electric field.
The basic properties of conductors allow us to describe many physical phenomena. Consider the following man standing inside a thin metal wire frame. Why is it that he does not flinch even while sparks are flying from a Tesla coil held at hundreds of thousands of volts?

Contents
Basic Properties of Conductors
The easiest way to describe conductors in electrostatic terms is with the following fundamental property.
Conductor Property 1.
Inside the material of a conductor at equilibrium, the electric field is always zero.
Since charge is always free to flow until it reaches an equilibrium, the electric field must be zero for the very simple reason that if electric field were nonzero, the charge would move. Now, if the conductor is disturbed by an external field (suppose that an external electric charge was brought close), the charges in the conductor will move, but after a short instant, the charges will reorient themselves into a stable, equilibrium configuration in which the electric field is zero. In general, the reorientation happens quite quickly, so to a good approximation the charges inside a conductor can be thought of as moving essentially instantaneously.
Several corollaries immediately follow from Property 1.
Since the the electric field is zero, the electric potential must be constant. In other words, a conductor is an equipotential surface. Recall that
\[ \Delta V = \int \textbf{E} \cdot d\textbf{l}, \]
but \( \textbf{E} = 0 \), so \( \Delta V = 0 \).
Conductor Property 2.
Inside the material of a conductor at equilibrium, the potential difference between any two points is zero.
Since the electric field inside a conductor is zero (\( \mathbf{E} = 0 \), it follows directly from the differential form of Gauss's law that there can also be no net charge \(\rho = 0 \) inside a conductor. However, some charge can reside on the surface of the conductor, where the charges are held from escaping the material entirely.
Conductor Property 3.
Inside the material of a conductor at equilibrium, there is no net charge any any point inside the conductor. All net charge (if any) resides on the surface or surfaces of the conductor.
Although there is charge on the surface of a conductor, it is locked in a static configuration at equilibrium. As a result, the electric field at the surface of the conductor must be perpendicular to the surface. If the electric field had any component parallel to the surface, then charge would flow along the surface, which would contradict the assumption that it is in equilibrium.
Conductor Property 4.
The electric field at the surface of a conductor at equilibrium is perpendicular to the surface.
Although the distribution of the induced charge is not always easy to calculate directly, it is possible to establish some general principles about the interaction of conductors and internal and external charges.
A collection of objects with total charge \( Q \) is placed inside of a hollow conductor that is initially neutral. What is the total charge on (a) the inner and (b) the outer surfaces of the conductor?
Between the two surfaces of the conductor, the electric field is zero, so Gauss's law gives that the total charge contained within a Gaussian surface enveloping the inner surface and the charged objects must be zero. Therefore, the inner surface must contain charge \( - Q \). Since the conductor is initially neutral, the outer surface must contain charge \( Q \).
A collection of objects with total charge \( Q \) is placed inside of a spherical hollow conductor that is initially neutral. What is the field outside of the conductor?
As in the previous example, the inner surface acquires induced charge \( -Q \), and the outer surface acquires induced charge \( Q \). But what is the distribution of the induced charge? Consider what would happen if we were somehow able to remove the outer surface charge \( Q \)—on their own, the charge from the inner surface induced charge cancels with the charge from the charged objects at all of the points outside of the cavity. Thus, the charge \( Q \) on the outer cavity simply redistributes uniformly as it would on a uniformly charged sphere. Therefore, the field outside of the conductor simply looks like that of a uniformly charged sphere of charge \( Q \). [1]
Note that the geometry of the inner surface and the positions of the charged objects was irrelevant. In other words, a hollow conductor "hides" the geometry of anything inside the sphere. You would only be able to ascertain the outer geometry due to the external field formed from the charge \( Q \) on the spherical outer surface, but you would not be able to determine the anything about the charges contained in the inner surface and cavity.
Electrostatic Shielding
One of the key phenomena involving conductors is electrostatic shielding. No matter what charge is brought close to an ideal conductor, the charges inside the conductor will always reorient themselves, by definition, so that \( \textbf{E} = 0 \) inside the conductor. This means that the surfaces of the conductor will become charged, but the induced charge will be distributed such that sum of the total field from the surfaces of the conductor and the field from the external charge is zero inside the conductor.
Therefore, a conductor with a hollow cavity can be used to shield an object from external electrostatic fields, as illustrated by the man standing unscathed inside the Faraday cage at the beginning of this Wiki. (Even though the material that makes up the cage might look scant, there is still enough such that the field inside the cage is minimal.) It must be the case that \( \textbf{E} = 0 \) inside the cavity because certainly \( \textbf{E} = 0 \) inside a solid conductor. Removal of material from the inside of the solid conductor can be done without disturbing the charges on the outer surface, thus producing a hollow conductor which also has the property \( \textbf{E} = 0 \) inside. Alternatively, there is also a proof of the same fact due to Gauss' law, which is left as an exercise.
An electric field is uniform throughout a certain region of space. Its magnitude is \(10~\mbox{V/m}\). A conducting sphere of radius \(R=1~\mbox{cm} \) and charge \(Q=1~\mu\mbox{C}\) is then placed in this region. Determine the magnitude of the electric field at the center of the sphere.
Details and assumptions
- \(k=\frac{1}{4\pi \epsilon_{0}}=9\times 10^{9}~\mbox{N m}^{2}/\mbox{C}^{2} \)
Laplace's Equation and Induced Charge
Suppose one wishes to determine completely the field of some charges and conductors. Equivalently, all one needs is the electric potential \( V \) defined as \( \mathbf{E} = - \nabla V \). In the empty space surrounding the conductors, Gauss' law implies that \( \nabla \cdot \mathbf{E} = 0 \), so
\[ \nabla^2 V = 0,\]
a result known as Laplace's equation. In principle, given the potential of each conductor in the system, one can solve for \( V \) everywhere. In some ways, Laplace's equation represents the most general possible statement of Coulomb's law (and, equivalently, Gauss's law).
Note that to arrive at a unique solution, the potential of the conductors must be specified. After all, Laplace's equation does not "know" if there is a conductor sitting somewhere. Information that must be specified about the potentials the system are known as the boundary conditions. In addition, one must usually also specify that the potential vanishes at infinity. For instance, if a conducting sheet is placed on the \( xy \)-plane, the corresponding boundary conditions would include that the potential is constant at \( z = 0 \) (\(V(z = 0) = V_0 \) for some constant \(V_0 \) ) and that the potential goes to zero as \( x^2 + y^2 + z^2 \) becomes large.
Discussion on general techniques for solving Laplace's equation is deferred to the references at the end of this Wiki. Regardless, in many cases, Laplace's equation is impractical to solve directly. Except in a handful of special cases, it has no closed-form analytic solution, and even when neat solutions exist, they are not always easy to find. Instead, we focus on one of many clever methods for indirectly arriving at a solution to Laplace's equation. One key mathematical result that simplifies things greatly is the so-called uniqueness theorem.
Uniqueness theorem. If there exists a valid solution \( V(\textbf{r}) \) satisfying the boundary conditions, then \( V \) is the only solution.
How does the uniqueness theorem help? If one can, say, find a valid configuration of charges that creates a potential satisfying Laplace's equations and the boundary conditions, then the potential associated with that configuration must be the only possible solution to Laplace's equation, no matter how one arrives at that solution. Fortunately, it turns out that simple guessing and reasoning often allows us to arrive at the correct answer, which must be the only answer by the uniqueness theorem. Consider the following problem.

A point charge of charge \( q \) is brought a distance \( d \) away from an infinite conducting sheet. What is the distribution of charge on the sheet and the resulting electric field?
The conducting sheet imposes the requirement that the potential along its surface must be constant. Equivalently, the electric field must be perpendicular at all points along the sheet. I claim that we already know one such distribution that satisfies this condition: the system of two opposite point charges.

If a point charge of charge \( -q \) is placed a distance \( d \) from the sheet directly across from the first charge, then the resulting potential satisfies the boundary condition, as the plane dividing the two charges is an equipotential, with field lines perpendicular to the plane. (Of course, it must satisfy Laplace's equation because it is a valid electrostatic distribution.) It follows from the uniqueness theorem that this must must be the only solution to the system. Therefore, the potential and electric field above the sheet are identical to that of the two-charge system.
However, the uniqueness theorem says nothing about what happens below the sheet, where the field must be zero. We can reason that from far away, the sheet looks a conducting sphere, inside which the field vanishes.
Meanwhile, the charge distribution can be found simply from using Gauss's law, which gives that the surface charge density must be \( \sigma = \epsilon_0 E \), where \( E \) is the component of the electric field perpendicular to the sheet at that point. (The precise calculation of \( E \) is left as an exercise for the reader.)
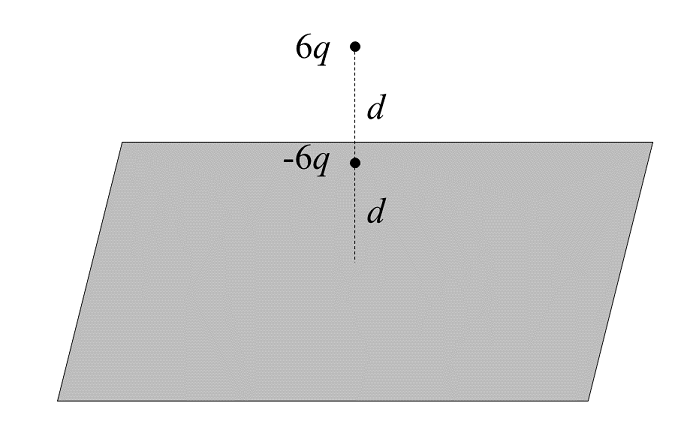
Two charges are placed above an infinite conducting sheet as shown. The first has charge \( -6q \) and is placed a distance \( d \) above the sheet, whereas the second has charge \( 6q \) and is placed a distance \( d \) directly above the first (so that it is a total distance \( 2d \) away from the sheet).
Where \( k = 1/(4\pi\epsilon_0) \), suppose \( F = C \cdot kq^2/d^2 \) represents the magnitude of the force on the first charge (of charge \( -6q \)). What is \( C \)?
References
[1] There is one slight subtlety to this argument, namely the claim that the inner surface induced charge must cancel the cavity charge for points outside of the conductor. This may not be true a priori, but in the end, since there exists a distribution such that the charges cancel, the uniqueness theorem tells us that this must be the correct distribution.
[2] Griffiths, D.J. Electricity and Magnetism. Fourth edition. Pearson, 2014.
[3] Purcell, E.M. Electricity and Magnetism. Third edition. Cambridge University Press, 2013.