Congruent and Similar Triangles
In mathematics, we say that two objects are similar if they have the same shape, but not necessarily the same size. This means that we can obtain one figure from the other through a process of expansion or contraction, possibly followed by translation, rotation or reflection. If the objects also have the same size, they are congruent.
Contents
Identify Congruent Triangles
Two triangles are congruent if they have the same three sides and exactly the same three angles. We have the methods of SSS (side-side-side), SAS (side-angle-side) and ASA (angle-side-angle). Note that for congruent triangles, the sides refer to having the exact same length. The LaTex symbol for congruence is \(\cong\) written as \cong.
SSS: Because we are working with triangles, if we are given the same three sides, then we know that they have the same three angles through the process of solving triangles. Thus, two triangles with the same sides will be congruent.
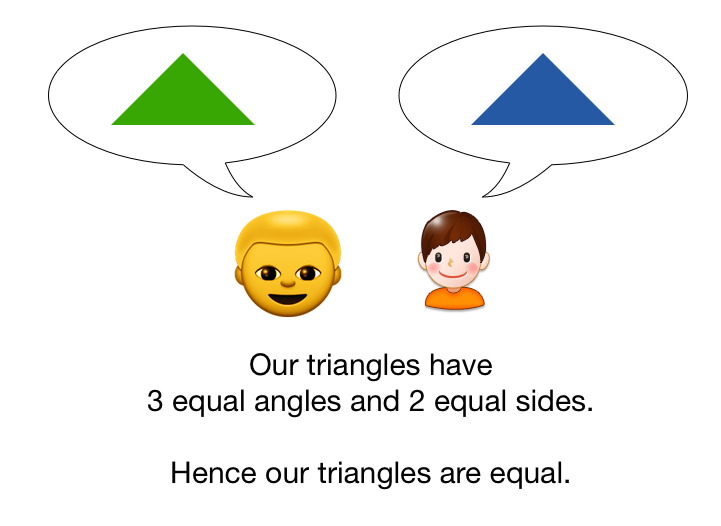
(Note: If two triangles have three equal angles, they need not be congruent. All that we know is these triangles are similar.)SAS: "Side, Angle, Side". It is a specific scenario to solve a triangle when we are given 2 sides of a triangle and an angle in between them.
(Note: If you try to use angle-side-side, that will make an ASS out of you. These triangles need not be congruent, or similar. See ambiguous case of sine rule for more information.)ASA: "Angle, Side, Angle". It is not necessary that the side be between the angles, since by knowing two angles, we also know the third.
Identify Similar Triangles
We have the methods SSS (side-side-side), SAS (side-angle-side), and AAA (angle-angle-angle), to prove that two triangles are similar. Note that in comparison with congruent figures, side here refers to having the same ratio of side lengths. Also, note that the method AAA is equivalent to AA, since the sum of angles in a triangle is equal to \(180^\circ\). The symbol is \(\Huge \color{red}{\text{~} }\) for similar.
SSS:
SAS:
AAA:
Compare Similar Triangles
In mathematics, we say that two objects are similar if they have the same shape, but not necessarily the same size. This means that we can obtain one figure from the other through a process of expansion or contraction, possibly followed by translation, rotation or reflection. If the objects also have the same size, they are congruent.
We have the methods SSS (side-side-side), SAS (side-angle-side), ASA (angle-side-angle), AAS (angle-angle-side) and AAA (angle-angle-angle), to prove that two triangles are similar. Note that in comparison with congruent figures, side here refers to having the same ratio of side lengths. Also, note that the method AAA is equivalent to AA, since the sum of angles in a triangle is equal to \(180^\circ\).
Area and Perimeter Relations
If two triangles are congruent, then they will have the same area and perimeter.
If two triangles are similar in the ratio \(R\), then the ratio of their perimeter would be \(R\) and the ratio of their area would be \(R^2\).
Problem Solving - Basic
Given that an acute triangle \(ABC\) has two known sides of lengths 7 and 8, respectively, and that the angle in between them is 33 degrees, solve the triangle.
It's much easier to visualize the triangle once we sketch out the triangle (note: figure not drawn up to scale).

Solving for the third side of the triangle by the cosine rule, we have \( a^2=b^2+c^2-2bc\cos(A) \) with \(b = 8, c= 7,\) and \(A = 33^\circ.\) Therefore, \(a \approx 4.3668. \)
Then we can solve for the rest of the triangle by the sine rule:
\[\begin{align} \frac a{\sin(A)} &= \frac b{\sin(B) } = \frac c{\sin(C)} \\\\ \frac{4.3668}{\sin(33^\circ)} &= \frac8{\sin(B)} = \frac 7{\sin(C)}. \end{align} \]
Setting for \(\sin(B) \) and \(\sin(C) \) separately as the subject yields \(B = 86.183^\circ, C = 60.816^\circ.\ _\square\)
Problem Solving - Intermediate
Two lines are drawn within a triangle such that they are both parallel to the triangle's base. The lower of the two lines passes through the intersection point of the diagonals of the trapezoid containing the upper of the two lines and the base of the triangle. The resulting blue triangle, in the diagram below left, has an area equal to the combined area of the \(2\) red triangles.

If, in the image above right, the number 9 indicates the area of the yellow triangle and the number 20 indicates the area of the orange trapezoid, what is the area of the green trapezoid?