Cosecant and Secant Graphs
Contents
Secant and Cosecant Graphs
From the definition of the secant and cosecant functions, we have
\[\sec( \theta) = \frac{1}{\cos(\theta)},\quad \csc( \theta) = \frac{1}{\sin(\theta)}.\]
This shows \(\sec(\theta)\) is not defined for values of \(\theta\) such that \(\cos(\theta) = 0\). From the graph of the cosine function we see that \(\cos(\theta) = 0\) when \(\theta = \frac{\pi}{2} + k\pi\) for any integer \(k\), which implies that the secant function has vertical asymptotes at these values of \(\theta\). The graph of the secant function is as follows:

Similarly, \(\csc(\theta)\) is not defined for values of \(\theta\) such that \(\sin(\theta) = 0\), which occurs for \(\theta = 0+ k\pi\) for any integer \(k\). Therefore, the cosecant function has vertical asymptotes at these values of \(\theta\). The graph of the cosecant function is as follows:
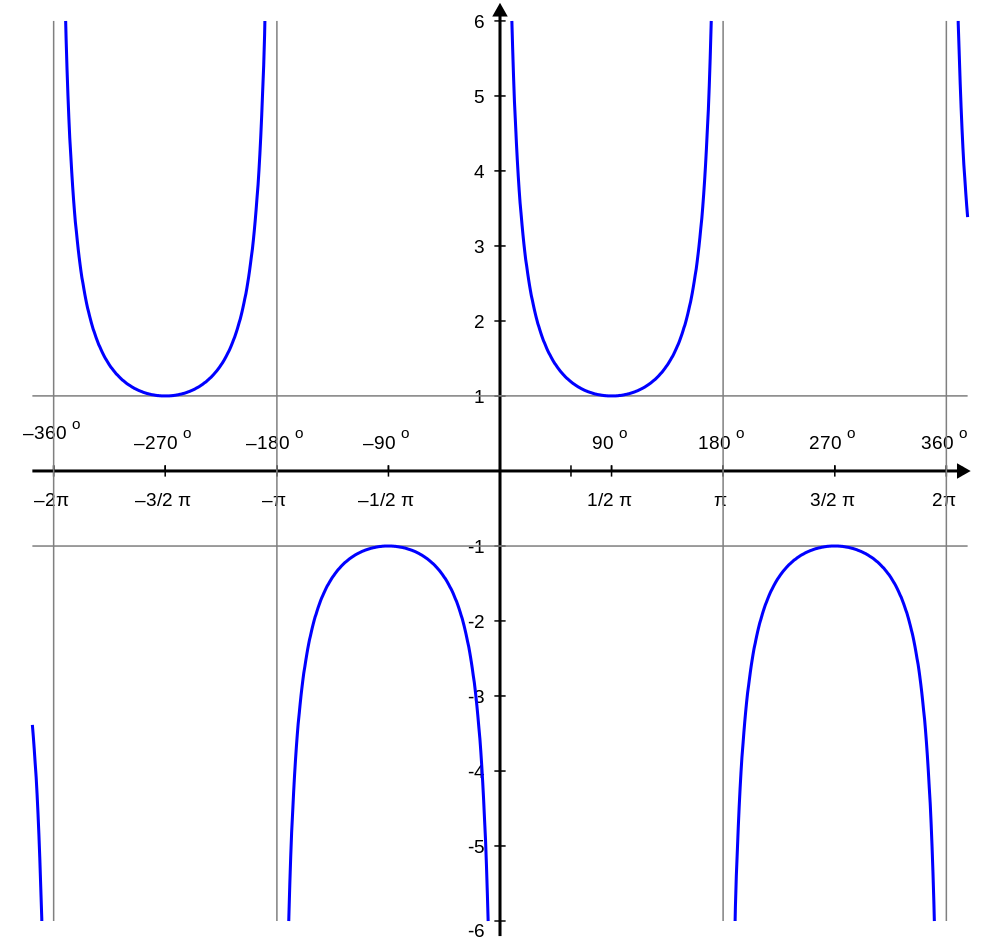
Properties
The secant and cosecant graphs satisfy the following properties:
- range: \( (-\infty, -1] \cup [1, \infty) \)
- period: \(2\pi.\)
From the graphs of the secant and cosecant functions, we see that secant is an even function (like cosine) and cosecant is an odd function (like sine). Also, the period of secant and cosecant are the same as the period of cosine and sine, which is \(2\pi\). In trigonometric identities, we will see how to prove the periodicity of these functions using trigonometric identities.
From the graphs of the tangent and cotangent functions, we see that the periods of secant and cosecant are both \(2\pi\).
Examples
What values of \(\theta\) in the interval \([0, 2\pi]\) satisfy \(\sec(\theta) = \csc(\theta)?\) Can we see this from the graphs of the secant and cosecant functions?
From the definitions of secant and cosecant, we have
\[\begin{align} \sec(\theta) &= \csc(\theta)\\ \frac{1}{\cos(\theta)} &= \frac{1}{\sin(\theta)}\\ \sin(\theta) &= \cos(\theta), \end{align}\]
which in the interval \(\theta \in [0, 2\pi]\) is satisfied for \(\theta = \frac{\pi}{4}, \frac{5\pi}{4}\).
We could also see this from the graphs of the secant and cosecant functions since the points of intersection occur for \(\theta = \frac{\pi}{4}, \frac{5\pi}{4}\). \(_\square\)
