Electric Dipoles

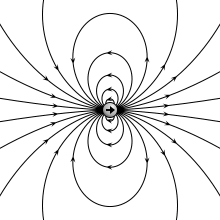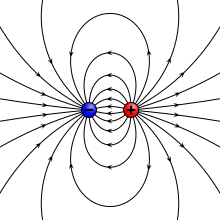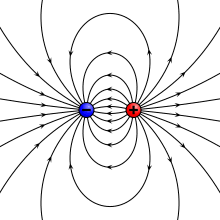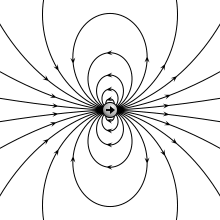Two charges are brought closer together. In the limit where the distance between them goes to zero, the become an ideal electric dipole and are represented simply with their dipole vector. ^[1]

An electric dipole is composed of two electric charges with opposite signs brought very close together. An ideal electric dipole is one in which the two charges are only infinitesimally separated. Equations defined particularly for electric dipoles are defined in terms of the electric dipole moment $(\vec{p}).$

The electric dipole moment for two charges $+q$ and $-q$ separated by a displacement vector $\vec{d}$ is

$$\vec{p} = q\vec{d}$$

If an electric dipole is placed in an external electric field the charges will feel forces in opposite directions by virtue of their opposite signs, causing a rotation if the two charges remain bound to one another. Hence, the forces actually manifest themselves as a torque.

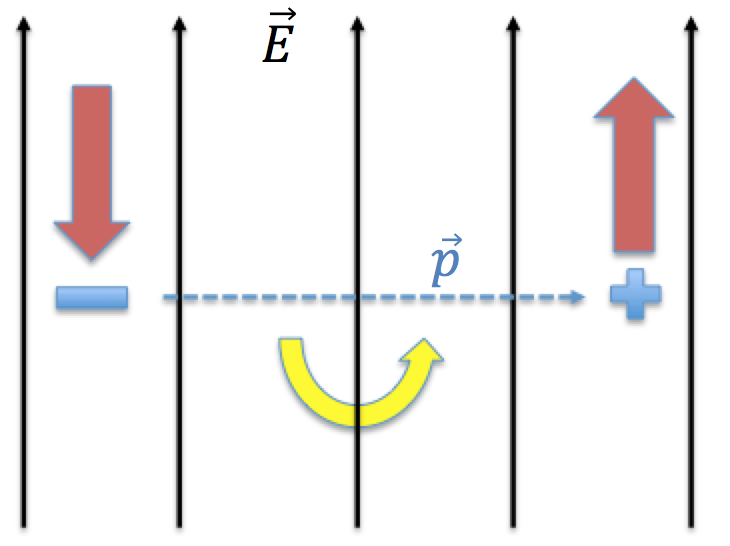The black external electric field causes red forces in opposite directions on the charges, resulting in rotation of the blue dipole moment in the direction indicated by the yellow arrow.

Since the torque is largest when $\vec{p}$ is perpendicular to $\vec{E}$ and decreases as the two vectors become more parallel, it is best modeled as the cross product between the two vectors.

The torque on a dipole $\vec{p}$ placed in an external field $\vec{E}$ is

$$\tau = \vec{p} \times \vec{E}$$

Two charges $+Q$ and $-Q$ are placed at $x = 1\text{ m}$ and $x = -1\text{ m}$ respectively in an external field $\vec{E} = 3 \hat{x} + 4 \hat{y}.$ What is the torque on the dipole?

---

In order to evaluate the cross product, write down the dipole.

$$\vec{p} = q\vec{d} = (Q) (2 \hat{x}) = 2Q\hat{x}$$

Now evaluate the cross product.

$$\tau = \vec{p} \times \vec{E} =( 2Q\hat{x}) \times (3 \hat{x} + 4 \hat{y}) = (8Q \text{ Nm})\hat{z}$$

The dipole wants to rotate until its moment points in the same direction as the external electric field. This orientation thus represents the potential minimum, and the potential energy increases as the angle between the dipole moment and the external field increases.

$$U=-\vec{p}\bullet\vec{E}$$

How much work is required to flip an electric dipole from its potential minimum to an orientation antiparallel to the external field?

---

Recall that work is defined in terms of potential energy according to the work-energy theorem.

$$W=-\Delta U = - (U_f -U_0) = -[pE\cos(180^\circ) - pE\cos(0^\circ) ] = 2pE$$

1. Geek3, . VFPt dipole animation electric. Retrieved June 8, 2016, from https://commons.wikimedia.org/wiki/File:VFPt_dipole_animation_electric.gif