Epsilon-Delta Definition of a Limit
In calculus, the \(\varepsilon\)-\(\delta\) definition of a limit is an algebraically precise formulation of evaluating the limit of a function. Informally, the definition states that a limit \(L\) of a function at a point \(x_0\) exists if no matter how \(x_0 \) is approached, the values returned by the function will always approach \(L\). This definition is consistent with methods used to evaluate limits in elementary calculus, but the mathematically rigorous language associated with it appears in higher-level analysis. The \(\varepsilon\)-\(\delta\) definition is also useful when trying to show the continuity of a function.
In this article, we will be proving all the limits using Epsilon-Delta limits.
Contents
Formal Definition of Epsilon-Delta Limits
Limit of a function \((\varepsilon\)-\(\delta\) definition\()\)
Let \(f(x)\) be a function defined on an open interval around \(x_0\) \(\big(f(x_0)\) need not be defined\(\big).\) We say that the limit of \(f(x)\) as \(x\) approaches \(x_0\) is \(L\), i.e.
\[\lim _{ x \to x_{0} }{f(x) } = L,\]
if for every \(\varepsilon > 0 \) there exists \(\delta >0 \) such that for all \(x\)
\[ 0 < \left| x - x_{0} \right |<\delta \textrm{ } \implies \textrm{ } \left |f(x) - L \right| < \varepsilon.\]
In other words, the definition states that we can make values returned by the function \(f(x)\) as close as we would like to the value \(L\) by using only the points in a small enough interval around \(x_0\). One helpful interpretation of this definition is visualizing an exchange between two parties, Alice and Bob. First, Alice challenges Bob, "I want to ensure that the values of \(f(x)\) will be no farther than \(\varepsilon > 0\) from \(L\)." If the limit exists and is indeed \(L\), then Bob will be able to respond by giving her a value of \(\delta\), "If for all points \(x\) is within a \(\delta\)-radius interval of \(x_0\), then \(f(x)\) will always be within an \(\varepsilon\)-interval of \(L\)." If the limit exists, then Bob will be able to respond to Alice's challenge no matter how small she chooses \(\varepsilon.\)
For example, in the graph for function \(f(x)\) below, if Alice gives Bob the value \( \varepsilon \), then Bob gives her the number \(\delta\) such that for any \(x\) in the open interval \( ( x_{0} - \delta, x_0 + \delta ) \), the value of \(f(x)\) lies in the interval \( ( L - \varepsilon, L + \varepsilon) \). In this example, as Alice makes \(\varepsilon \) smaller and smaller, Bob can always find a smaller \(\delta\) satisfying this property, which shows that the limit exists.
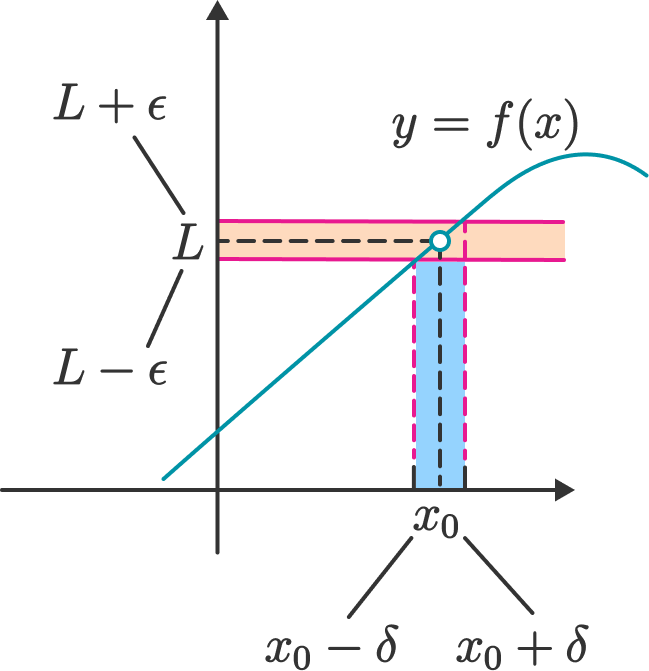
As the exchange between Alice and Bob demonstrates, Alice begins by giving a value of \(\varepsilon\) and then after knowing this value, Bob can determine a corresponding value for \(\delta\). Because of this ordering of events, the value of \(\delta\) is often given as a function of \(\varepsilon\). Note that there may be multiple values of \(\delta\) that Bob can give.
If there is any value of \(\varepsilon\) for which Bob cannot find a corresponding \(\delta\), then the limit does not exist!
For the function \(f(x) = 3x^2 + 2x + 1,\) Alice wants Bob to show that \(\displaystyle \lim_{x \rightarrow 2} f(x) = 17\) using the \(\varepsilon\)-\(\delta\) definition of a limit.
Alice says, "I bet you can't choose a real number \(\delta\) so that for all \(x\) in \((2 - \delta, 2 + \delta)\), we'll have that \(\left|f(x) - 17\right| < 0.5\)."
Which of the following four choices is the largest \(\delta\) that Bob could give so that he completes Alice's challenge?
Infinite Limit for finite \(x\)
Let \(f\) be a function defined on some open interval that contains the number \(x_0\) \(\big(f(x_0)\) need not be defined\(\big).\) We say that the limit of \(f(x)\) as \(x\) approaches \(x_0\) diverges to infinity, i.e. \[ \lim_{x\to x_0} f(x) = \infty \] if for every positive number \(M\) there exists \(\delta>0\) such that for all \(x\) \[ 0 < |x-x_0 | < \delta\textrm{ } \implies \textrm{ } f(x) > M \]
This says that the values of \(f(x) \) can be made arbitrarily large by taking \(x\) close enough to \(x_0\).
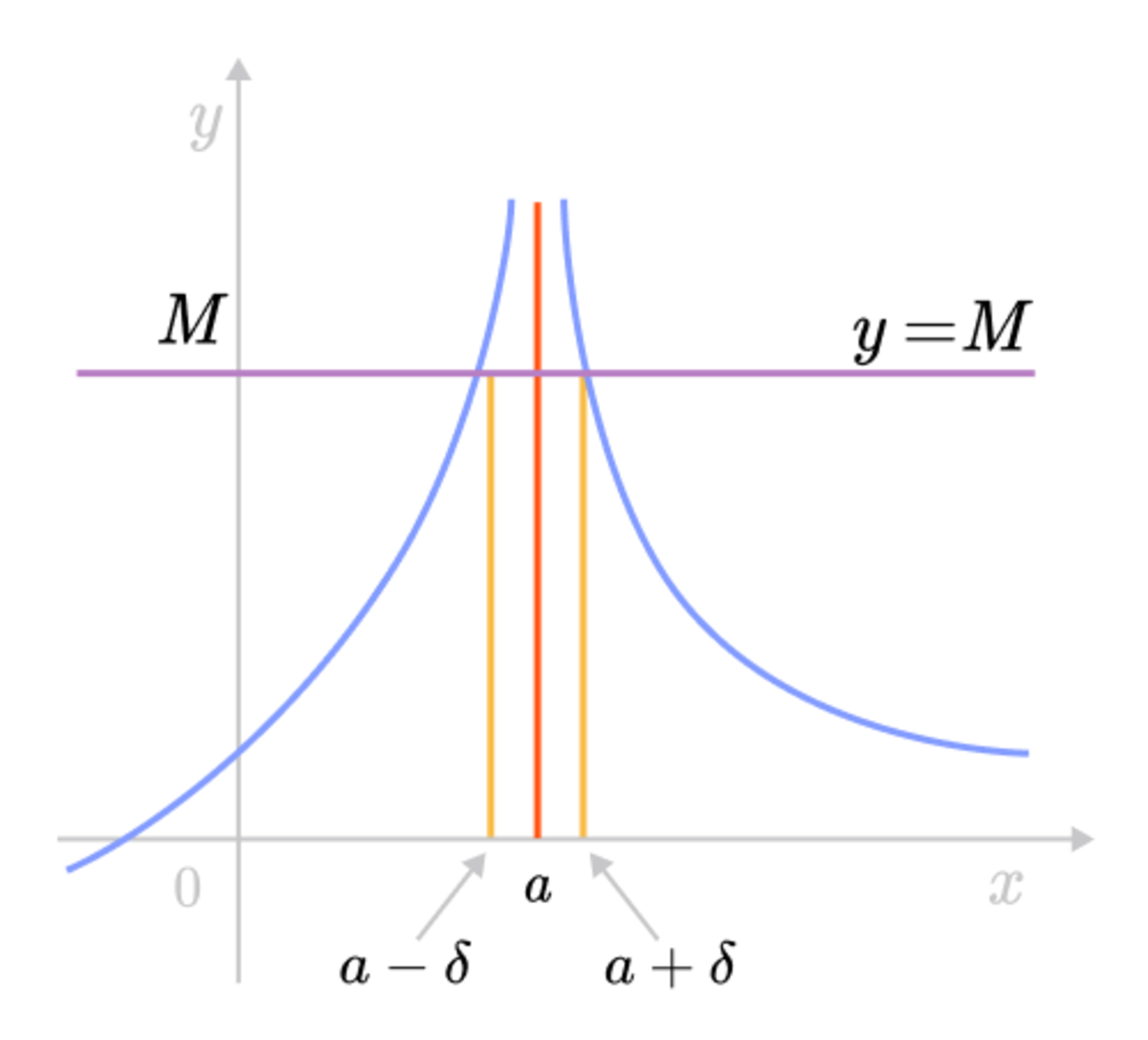
For example, in the graph for the function \(f(x) \). For any horizontal line \(y = M > 0\), we can find a number \(\delta>0\) such that for any interval of \(x\) in the interval \((x_0 - \delta, x_0 + \delta) \) but \(x\ne x_0 \), then the curve \(y = f(x) \) lies above the line \(y = M\). We can see that for any larger \(M \) chosen, a smaller value of \(\delta\) is needed.
Finite Limit at Infinity
In the previous sections, we used the terms arbitrarily large to define limits informally. Even though they give a good intution about the description of limits at infinity, they are not mathematically rigorous. Let us try to define them formally.
\(f\) is said to have a limit at infinity, if there exists a real number \(L \) such that for all \(\epsilon > 0\), there exists \(N>0\) such that \( |f(x) - L | < \epsilon \) for all \(x>N\). In other words, \[ \lim_{x\to\infty} f(x) = L . \]
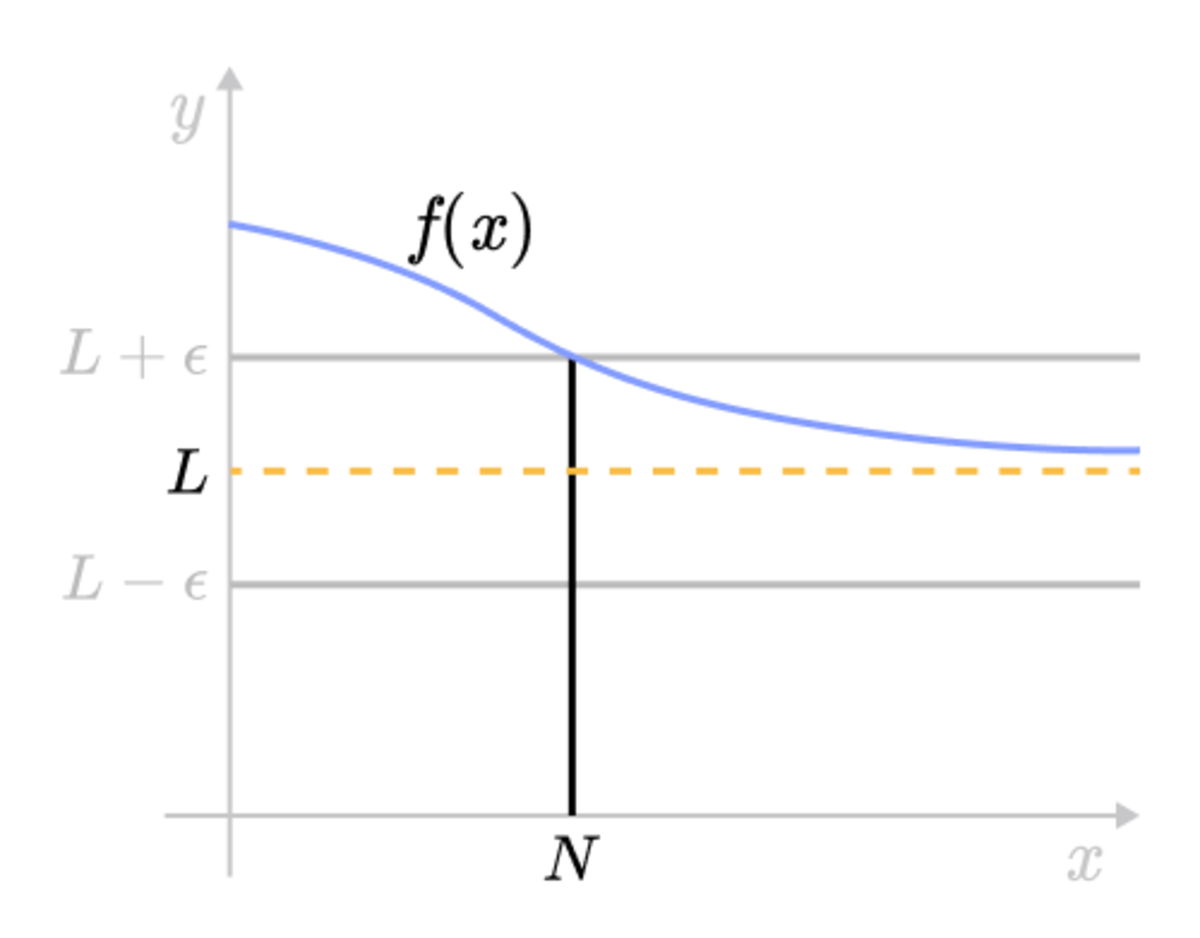
For example, in the graph for the function \(f(x) \). For sufficiently large value of \(N\), we can find the interval of \(y\) to be \( (L- \epsilon, L + \epsilon) \) but \(y= L \), then the curve \(y = f(x) \) lies between the two lines \(y = L - \epsilon\) and \(y = L + \epsilon\). We can see that for for any larger \(N\) chosen, a smaller value of \(\epsilon\) is needed.
Show that \(\lim \limits_{x \rightarrow \infty} \left(7 - \frac1x\right) = 7.\)
Let \(\epsilon > 0\), then \(N = \frac1\epsilon\). Then, for all \(x>N\), \[ \left |7 - \frac1x - 7\right| = \left | \frac1x \right | = \frac1x < \frac1N = \epsilon \] Hence, our claim. \(_\square\)
Infinite Limit at Infinity
\(f\) is said to have an infinite limit at infinity, if for all \(M > 0\), there exists an \(N> 0\) such that \(f(x) > M \) for all \(x> N\). That is, \(\lim \limits_{x\to\infty} f(x) = \infty\).
Analogously, \(f\) is said to have a negative infinite limit at infinity, if for all \(M < 0\), there exists an \(N> 0\) such that \(f(x) < M \) for all \(x> N\). That is, \(\lim \limits_{x\to\infty} f(x) = -\infty\).
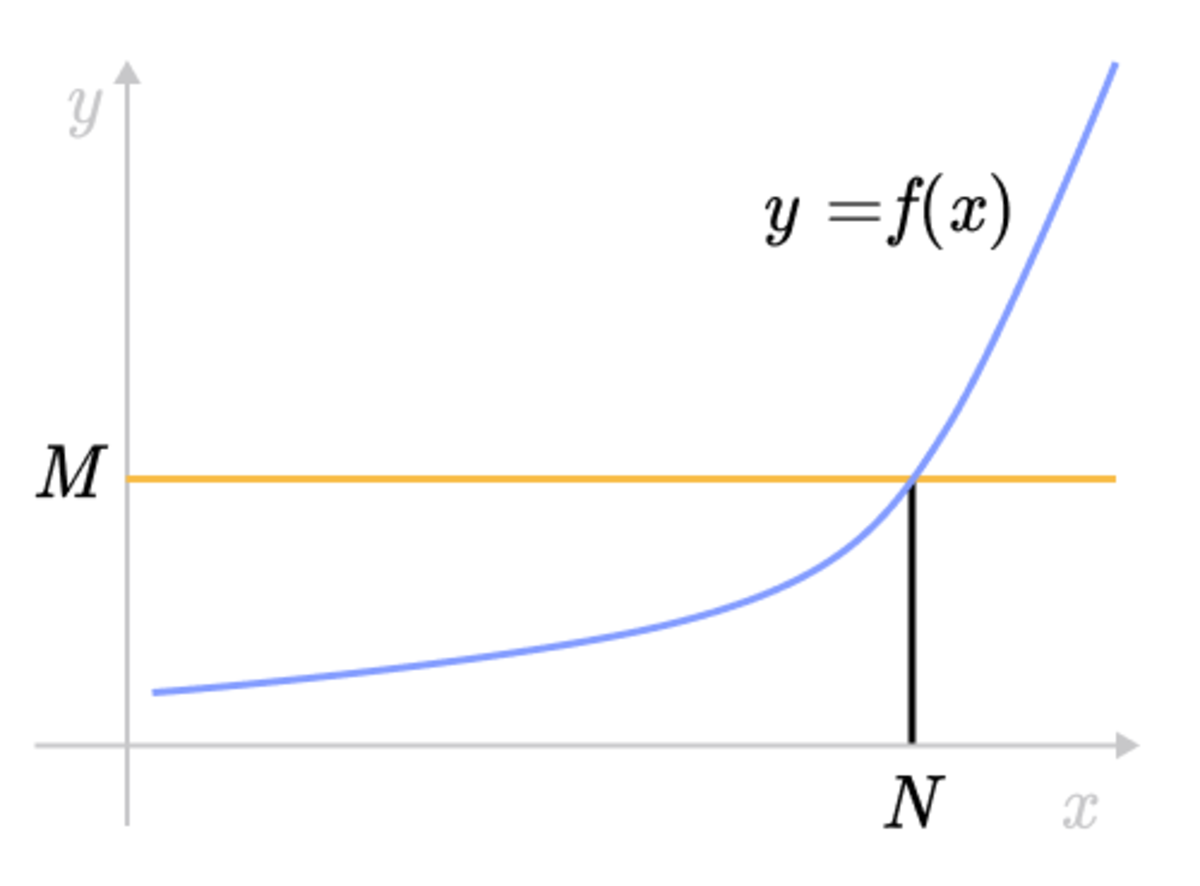
For example, in the graph for the function \(f(x) \). For sufficiently large value of \(N\), we can find a value \(M>0\) such that \(f(x) > M\) for all \(x> N\).
Use the formal definition of infinite limit at infinity, prove that \( \lim \limits_{x\to\infty} x^9 = \infty \).
Let \(M > 0\), and let \(N = \sqrt[9]{M} \). Then for all \(x> N\), \[ x^9 > N^9 = \left( \sqrt[9]{M} \right)^9 = M. \quad _\square \]
From the example above, we know that \( \lim \limits_{x\to\infty} x^9 = \infty \). Without extracting out the scalar multiple, prove \( \lim \limits_{x\to\infty} 9x^9 = \infty \) using the formal definition of infinite limit at infinity as well.
Let \(M > 0\), and let \(N = \sqrt[9]{\frac M9} \). Then for all \(x> N\), \[ 9x^9 > 9N^9 = 9\left( \sqrt[9]{M} \right)^9 = M. \quad _\square \]
Finding Delta given an Epsilon
In general, to prove a limit using the \(\varepsilon\)-\(\delta\) technique, we must find an expression for \(\delta\) and then show that the desired inequalities hold. The expression for \(\delta\) is most often in terms of \(\varepsilon,\) though sometimes it is also a constant or a more complicated expression. Below are a few examples that demonstrate this property.
Show that \(\displaystyle \lim_{x \rightarrow \pi} x = \pi.\)
Let \(f(x) = x.\) First we need to determine what value our \(\delta\) is going to have. When \(\vert x - \pi \vert < \delta\) we want \(\vert f(x) - \pi \vert < \varepsilon.\) We know that \(\vert f(x) - \pi \vert = \vert x - \pi \vert < \delta,\) so taking \(\delta = \varepsilon\) will have the desired property.
There are other values of \(\delta\) we could have chosen, such as \(\delta = \frac{\varepsilon}{7}.\) Why would this value of \(\delta\) have also been acceptable? If \(\vert x - \pi\vert < \delta = \frac{\varepsilon}{7},\) then \(\vert f(x) - \pi \vert < \frac{\varepsilon}{7} < \varepsilon,\) as required. \(_\square\)
To show that a limit exists, we do not necessarily need to prove that the result holds for all \(\varepsilon,\) but it is sufficient to show that the result holds for all \(\varepsilon < k\) for any positive value \(k.\) This is because the \(\delta\) value for a particular \(\varepsilon = e\) is also a valid \(\delta\) for any \(\varepsilon > e.\)
Show that
\[\lim _{x \to 1} {(5x-3)} = 2.\]
In this example, we have \(x_{0} = 1\), \(f(x) = 5x -3\), and \(L = 2\) from the definition of limit given above. For any \(\varepsilon > 0\) chosen by Alice, Bob would like to find \(\delta >0\) such that if \(x\) is within distance \(\delta\) of \(x_{0} = 1\), i.e.
\[ \left|x-1\right|<\delta,\]
then \( f(x) \) is within distance \(\varepsilon\) of \(L=2\), i.e.
\[\left|f(x) - 2\right| < \varepsilon.\]
To find \(\delta\), Bob works backward from the \(\varepsilon\) inequality:
\[\begin{align} \left| (5x-3) - 2 \right| &= \left|5x-5\right| < \varepsilon \\ &= 5\left|x-1\right|<\varepsilon \\ &= \left|x-1\right| < \frac{\varepsilon}{5}. \end{align}\]
So Bob gives Alice the value of \(\delta = \frac{\varepsilon}{5}\). Then Alice can verify that if \( \left|x-1\right| <\delta = \frac{\varepsilon}{5}\) then
\[\left|(5x-3)-2\right| = \left|5x-5\right| = 5\left|x-1\right| < 5\left(\frac{\varepsilon}{5}\right) = \varepsilon. \ _\square\]
Prove that \(\displaystyle \lim_{x \rightarrow 7} (x^2 + 1) =50.\)
Let \(f(x) = x^2 + 1.\) We will first determine what our value of \(\delta\) should be. When \(\vert x - 7 \vert < \delta\) we have
\[\begin{array}{rl}\vert x^2 + 1 - 50 \vert & = \vert x^2 - 49\vert\\ & = \vert x-7 \vert \vert x + 7 \vert\\ & < \delta \vert x + 7 \vert. \end{array}\]
Assuming \(\vert x - 7\vert < 1,\) we have \(\vert x \vert < 8,\) which implies \(\vert x + 7 \vert < \vert x \vert + \vert 7 \vert = 15\) by the triangle inequality.
So, when we let \(\delta = \min\left( 1, \frac{\varepsilon}{15}\right),\) we will have
\[\begin{array}{rl}\vert x^2 + 1 - 50 \vert & < \delta \vert x + 7 \vert\\ & < 15 \delta\\ & < \varepsilon. \ _\square \end{array}\]
Using the \( \varepsilon\)-\(\delta\) definition, prove the following limit:
\[ \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1.\]
On the interval \( \left( - \frac{\pi}{2} , \frac{\pi}{2} \right) \), we have \(0 < \cos x < \frac{\sin x}{x} < 1\), which implies
\[ \begin{align} \left| \frac{\sin x}{x} -1 \right| & < 1 - \cos x\\ \left| \frac{\sin x}{x} -1 \right| & < 2\sin^2 \frac{x}{2} \\ &< \frac{x^2}{2}. \end{align} \]
Now, given \( \varepsilon >0 \), let \(\delta = \sqrt{\varepsilon}\). Then the calculation above shows that \( \lvert x - 0 \rvert < \delta = \sqrt{\varepsilon} \) implies
\[ \left| \frac{\sin x}{x} -1 \right| < \frac{x^2}{2} < \frac{ \sqrt{ \varepsilon} ^2}{2} < \varepsilon,\]
which completes the proof. Therefore,
\[ \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1. \ _\square\]
There are instances where the limit of \(f(x)\) as \(x\) approaches \(x_0\) increases or decreases without bound. In such cases, it is often said that the limit exists and the value is infinity (or negative infinity). However, some resources say that the limit does not exist in this instance, simply because this restriction makes other theorems in calculus slightly easier to state and remember.
In proving a limit goes to infinity when \(x\) approaches \(x_0\), the \(\varepsilon\)-\(\delta\) definition is not needed. Rather, we need only show that the function becomes arbitrarily large at values close to \(x_0.\)
Prove
\[ \lim_{x \rightarrow \infty} \frac{1}{x^2} = 0 .\]
Given \(\varepsilon,\) we need to choose \(\delta\) so that if \(x > \delta,\) then \(\left| \dfrac{1}{x^2} - 0\right| < \varepsilon.\)
Suppose \(\left|\frac{1}{x^2} - 0\right| < \varepsilon.\) In solving for \(x,\) we find that \(x > \frac{1}{\sqrt{\varepsilon}}.\) Therefore, for any challenge \(\varepsilon\) we are given, it is ensured that \(\left|\frac{1}{x^2} - 0\right| < \varepsilon\) so long as we choose \(\delta > \frac{1}{\sqrt{\varepsilon}}.\) Therefore \( \lim_{x \rightarrow \infty} \frac{1}{x^2} = 0. \ _\square \)
Prove
\[ \lim_{x \rightarrow 0} \frac{1}{x^2} = \infty .\]
We show that for any positive number \(L\), set \( \delta = \frac{1}{\sqrt{L}} \). Then, when \( | x - 0 | < \delta \), we have
\[ f(x) = \frac{ 1 } { x^2 } > \frac{ 1 } { \left( \frac{1}{ \sqrt{L} } \right)^ 2 } = L. \]
This shows that the values of the function becomes and stays arbitrarily large as \(x\) approaches zero, or \( \lim \limits_{x \rightarrow 0} \frac{1}{x^2} = \infty. \ _\square\)
Limit Does Not Exist
The \(\varepsilon\)-\(\delta\) definition can be used to show that the limit at a point does not exist. For the limit to exist, our definition says, "For every \(\varepsilon > 0\) there exists a \(\delta > 0\) such that if \(\vert x - x_0 \vert < \delta,\) then \(\vert f(x) - L \vert < \varepsilon.\)" This means that \(L\) is not the limit if there exists an \(\varepsilon > 0\) such that no choice of \(\delta > 0\) ensures \(\vert f(x) - L \vert < \varepsilon\) when \(\vert x - x_0 \vert < \delta.\)
Consider the function given by
\[ f(x) = \begin{cases} 1 && x > 0 \\ -1 && x < 0 .\end{cases} \]
Show that the limit at 0 does not exist.
This is almost obvious. We see that the "right-hand limit" is \(1,\) and the "left-hand limit" is \(-1.\) As such, it makes sense that the limit does not exist. Let's formally show it, using the \(\varepsilon\)-\(\delta\) language that we developed above.
Suppose that the limit at 0 exists and is equal to \(L \). Let \( \varepsilon = \frac{1}{2} \), with a corresponding \( \delta = \delta_\varepsilon > 0 \).
Since the limit exists, we know that for all \( y \in ( - \delta, \delta ) \), we have \( | f(y) - L | < \varepsilon = \frac{1}{2} \). However, we also have
\[ \begin{align} 2 & = \left| f\left( \frac{\delta}{2} \right) - f \left( - \frac{ \delta} { 2} \right) \right| \\ &= \left| f\left( \frac{\delta}{2} \right) - L + L - f \left( - \frac{ \delta} { 2} \right) \right| \\ & \leq \left| f\left( \frac{\delta}{2} \right) - L \right| + \left| L - f \left( - \frac{ \delta} { 2} \right) \right| \\ & \leq \frac{1}{2} + \frac{1}{2} \\ & = 1. \\ \end{align} \]
This is a contradiction, so our original assumption is not true. \(_\square\)
The above proof is easily adapted to show the following:
The limit at an interior point of the domain of a function exists if and only if the left-hand limit and the right-hand limit exist and are equal to each other.
Let \(f(x)\) be the function that is \(0\) when \(x\) is rational and \(1\) otherwise. Show that \(\displaystyle \lim_{x \rightarrow a} f(x)\) does not exist for any \(a.\)
Let \(a\) be a rational number. We know that \(f(a) = 0.\) Let \(\varepsilon = 0.5\) and \( \delta > 0.\) Since the irrational numbers are dense in the real numbers, we can find an irrational number \(b \in (a - \delta, a + \delta).\) \(\vert f(b) - f(a) \vert = 1 > \varepsilon,\) but \(\vert a - b \vert < \delta.\) Thus, \(f\) is not continuous at \(a.\) The result is similar if we consider \(a\) to be an irrational point. \(_\square\)
