Irrational Numbers
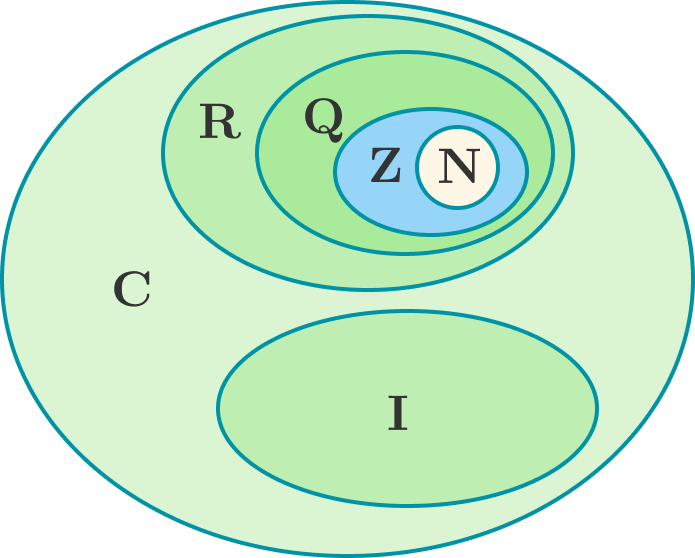
Irrational numbers are real numbers that cannot be expressed as the ratio of two integers. More formally, they cannot be expressed in the form of \(\frac pq\), where \(p\) and \(q\) are integers and \(q\neq 0\). This is in contrast with rational numbers, which can be expressed as the ratio of two integers. One characteristic of irrational numbers is that their decimal expansion does not repeat or terminate.
Contents
History
Main Article: History of Irrational Numbers
The first man to recognize the existence of irrational numbers might have died for his discovery. Hippassus of Metapontum was an ancient Greek philosopher of the Pythagorean school of thought. Supposedly, he tried to use his teacher's famous theorem \( a^{2}+b^{2}= c^{2}\) to find the length of the diagonal of a unit square. This revealed that a square's sides are incommensurable with its diagonal, and that this length cannot be expressed as the ratio of two integers. The other Pythagoreans believed dogmatically that only positive rational numbers could exist. They were so horrified by the idea of incommensurability that they threw Hippassus overboard on a sea voyage, and vowed to keep the existence of irrational numbers an official secret of their sect. However, there are good reasons to believe Hippassus's demise is merely an apocryphal myth. Historical documents referencing the incident are both sparse and written 800 years after the time of Pythagoras and Hippassus. It wasn't until approximately 300 years after Hippassus's time that Euclid would give his proof for the irrationality of \(\sqrt{2}.\)
The Pythagoreans had likely manually measured the diagonal of a unit square. However, they would have regarded such a measurement as an approximation close to a precise rational number that gave the true length of the diagonal. Before Hippassus, Pythagoreans had no reason to suspect that there were real numbers that in principle, not merely in practice, could not be measured or counted to. Numbers were the spiritual basis of their philosophy and religion for the Pythagoreans. Cosmology, physics, ethics, and spirituality were predicated on the premise that "all is number." They believed that all things--the number of stars in the sky, the pitches of musical scales, and the qualities of virtue--could all be described by and apprehended through rational numbers.
Examples of Irrational Numbers
Irrational numbers arise in many circumstances in mathematics. Examples include the following:
- The hypotenuse of a right triangle with base sides of length 1 has length \( \sqrt{2}\), which is irrational.
- More generally, \( \sqrt{D}\) is irrational for any integer \( D\) that is not a perfect square. For demonstration, we will prove that \(\sqrt 2\) is an irrational number in a later section Irrationality of \(\sqrt 2\).
- The ratio \(\pi\) of the circumference of a circle to its diameter is irrational.
- The base \(e\) of the natural logarithm is irrational.
Check out the following example for better understanding:
Is \( \frac{ 7 \sqrt{2+4} }{\sqrt{2} } \) rational or irrational?
We have
\[ \frac{ 7 \sqrt{2+4} }{\sqrt{2} } = \frac{ 7 \sqrt{6} }{\sqrt{2} } = 7 \sqrt{3}. \]
By property 2 above, \(\sqrt{3}\) is an irrational number since 3 is not a perfect square. Therefore \( 7 \sqrt{3} \) is an irrational number. \(_\square\)
Try the following problem:
Properties of Irrational Numbers
- Taking the sum of an irrational number and a rational number gives an irrational number. To see why this is true, suppose \(x\) is irrational, \(y\) is rational, and the sum \(x+y\) is a rational number \(z\). Then we have \(x = z-y\), and since the difference of two rational numbers is rational, this implies \(x\) is rational. This is a contradiction since \(x\) is irrational. Therefore, the sum \(x+y\) must be irrational.
- Multiplying an irrational number with any nonzero rational number gives an irrational number. We argue as above to show that if \(xy = z\) is rational, then \({x = \frac{z}{y}}\) is rational, contradicting the assumption that \(x\) is irrational. Therefore, the product \(xy\) must be irrational.
- The lowest common multiple (LCM) of two irrational numbers may or may not exist.
- The sum or the product of two irrational numbers may be rational; for example,
\[ \sqrt{2} \cdot \sqrt{2} = 2.\]
Therefore, unlike the set of rational numbers, the set of irrational numbers is not closed under multiplication.
Here are some examples based on the above properties:
Is \( \sqrt{36} \) rational or irrational?
Since \( \sqrt{36} =6, \) this is a rational number. \(_\square\)
Show that \( \sqrt{2} + \sqrt{3}\) is not rational.
We give a proof by contradiction. If \( \sqrt{2}+\sqrt{3}\) is rational, then \( (3-2) \times \frac {1}{\sqrt{3} + \sqrt{2}} = \sqrt{3}-\sqrt{2}\), implying \( \sqrt{3} - \sqrt{2}\) is also rational. Since \( \big(\sqrt{3} + \sqrt{2}\big) - \big(\sqrt{3}-\sqrt{2}\big) = 2 \sqrt{2}\), we obtain \( 2 \sqrt{2}\) is rational. Thus, \( 2 \sqrt{2} \times \frac {1}{2} = \sqrt{2}\) is also rational, which is a contradiction. \(_\square\)
We generalize the result above to show that \( \sqrt{D}\) is rational if and only if \( D\) is a perfect square.
Given integers \( n\) and \( m\), if \( n^{\frac {1}{m}}\) is rational, then \( n^{\frac {1}{m}}\) is an integer. In particular, the only rational \( m^\text{th}\) roots of integers \( n\) are the integers.
Let \( n^{\frac {1}{m}}= \frac {a}{b} \), where \( a\) and \( b\) are coprime integers. Then taking powers and clearing denominators gives \( b^m n = a^m \). If \( p\) is a prime that divides \( b\), then \( p\) divides \( b^m n\), so \( p \) divides \( a^m\) and thus \( p\) divides \( a\). Since \( a\) and \( b\) are coprime, there is no prime that divides both \( a\) and \( b\). Hence, no prime divides \( b\), implying \( b=1\). Therefore, \( n^{\frac {1}{m}} = a\) is an integer. \( _\square\)
Here are some problems to try:
Read the following statements:
1) \(\frac { e }{ \pi } \) is a rational number.
2) \(\frac { \pi }{ e } \) is an irrational number.
3) \(\frac { \pi+e }{ e } \) is a rational number.
Give your answer as the mean of the serial numbers of the statements which are true.
\(\big(\)E.g., if all statements are true, the answer is \(\frac { 1+2+3 }{ 3 } =2.\big)\)
\(\)
Details and Assumptions:
- \(e\) may not necessarily be the exponential constant and \(\pi \) may not necessarily be equal to 3.14159...
\[\Large \color{blue}{e},~~ \color{green}{\pi}\]
Find the lowest common multiple (LCM) of the two numbers above.
\(\)
Details and Assumptions:
- If you think that the existence of this LCM is unknown to humans, submit "Does not exist" as your answer.
- If you think that it is extremely close to zero, but not zero, then you may press "0".
- If you think that it is extremely close to one, but not one, then you may press "1".
\[\large \color{orange}{-6\pi} \color{black},~~ \color{green}{\pi}\]
Find the lowest common multiple (LCM) of the two numbers above.
To clarify, the LCM of two irrational numbers exists if and only if their ratio is rational.
Inspiration
Irrationality of \(\sqrt{2}\)
Below you can see the proof of the irrationality of \(\sqrt{2}.\)
Let's use the method known as proof by contradiction.
Let's say \(\sqrt{2}\) is a rational number:
\[\sqrt { 2 } =\frac { a }{ b},\]
where \(a\) and \(b\) are coprime integers, i.e. \(a\) and \(b\) do not have prime factors in common and \(\gcd\left( a,b \right) =1\). In other words, \(\frac { a }{ b }\) is an irreducible fraction.
Solving the equation above gives
\[\begin{align} \sqrt { 2 } &=\frac { a }{ b }\\ 2&=\frac { { a }^{ 2 } }{ { b }^{ 2 } } \\ \\ \Rightarrow a^2&=2{ b }^{ 2 }. \end{align}\]
As you can see, \({a}^{2}\) is even because it is the double of \({b}^{2}\). If \({a}^{2}\) is even \(a\) is also even because the square of an odd number is an odd number, and the square of an even number is an even number.
If \(a\) is even, we can write it as \(2c=a,\) which implies
\[\begin{align} 2{ b }^{ 2 } &={ a }^{ 2 }\\ &={ \left( 2c \right) }^{ 2 }\\ &={ 4c }^{ 2 }\\ \\ \Rightarrow { b }^{ 2 }&={ 2c }^{ 2 }. \end{align}\]
As you can see, \(b\) is also even by the same reason as \(a\) is. Wait! We have a contradiction here. We say that \(a\) and \(b\) are coprime integers, i.e \(\frac{a}{b}\) is irreducible, but \(a\) and \(b\) are both even numbers which can't form an irreducible fraction. Thus, this is an impossible fraction, so \(\sqrt{2}\) can't be written as the ratio of 2 integers. \(_\square\)