Ergodic Markov Chains
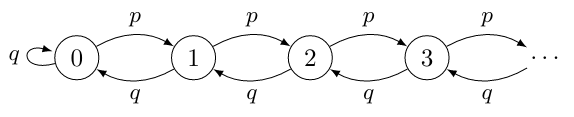 For \(p < \tfrac{1}{2}\) and \(q = 1 - p\), the random walk with reflection is an ergodic Markov chain
A Markov chain that is aperiodic and positive recurrent is known as ergodic. Ergodic Markov chains are, in some senses, the processes with the "nicest" behavior.
For \(p < \tfrac{1}{2}\) and \(q = 1 - p\), the random walk with reflection is an ergodic Markov chain
A Markov chain that is aperiodic and positive recurrent is known as ergodic. Ergodic Markov chains are, in some senses, the processes with the "nicest" behavior.
Contents
Definition
An ergodic Markov chain is an aperiodic Markov chain, all states of which are positive recurrent.
Properties
An irreducible Markov chain has a stationary distribution if and only if the Markov chain is ergodic. If the Markov chain is ergodic, the stationary distribution is unique.
Let \(X\) be an ergodic Markov chain with states \(1, \, 2, \dots, \, n\) and stationary distribution \((x_1, \, x_2, \dots, \, x_n)\). If the process begins at state \(k\), the expected number of steps \(E_k\) to return to state \(k\) is \(E_k = \dfrac{1}{x_k}\).
Many probabilities and expected values can be calculated for ergodic Markov chains by modeling them as absorbing Markov chains with one absorbing state. By changing one state in an ergodic Markov chain into an absorbing state, the chain immediately becomes an absorbing one, as ergodic Markov chains are irreducible (and therefore all states are connected to the absorbing state).