Graph Coloring and Chromatic Numbers
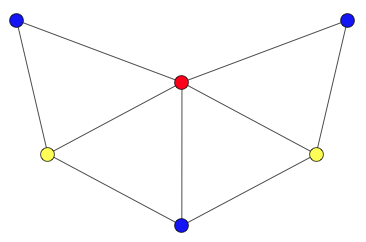 A graph coloring for a graph with 6 vertices. It is impossible to color the graph with 2 colors, so the graph has chromatic number 3.
A graph coloring for a graph with 6 vertices. It is impossible to color the graph with 2 colors, so the graph has chromatic number 3.
A graph coloring is an assignment of labels, called colors, to the vertices of a graph such that no two adjacent vertices share the same color. The chromatic number \(\chi(G)\) of a graph \(G\) is the minimal number of colors for which such an assignment is possible. Other types of colorings on graphs also exist, most notably edge colorings that may be subject to various constraints.
The study of graph colorings has historically been linked closely to that of planar graphs and the four color theorem, which is also the most famous graph coloring problem. That problem provided the original motivation for the development of algebraic graph theory and the study of graph invariants such as those discussed on this page. In modern times, many open problems in algebraic graph theory deal with the relation between chromatic polynomials and their graphs. Applications for solved problems have been found in areas such as computer science, information theory, and complexity theory. Many day-to-day problems, like minimizing conflicts in scheduling, are also equivalent to graph colorings.
Sudoku can be seen as a graph coloring problem, where the squares of the grid are vertices and the numbers are colors that must be different if in the same row, column, or \(3 \times 3\) grid (such vertices in the graph are connected by an edge). The sudoku is then a graph of 81 vertices and chromatic number 9. How many edges does this 81-vertex graph have?
Graph Colorings
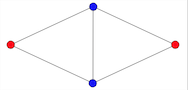 This graph is not 2-colorable
This graph is not 2-colorable
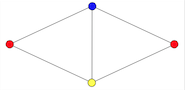 This graph is 3-colorable
This graph is 3-colorable
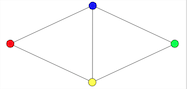 This graph is 4-colorable
This graph is 4-colorable
The chromatic number of a graph is the minimal number of colors for which a graph coloring is possible. This definition is a bit nuanced though, as it is generally not immediate what the minimal number is. For certain types of graphs, such as complete (\(K_n\)) or bipartite (\(K_{m,n}\)), there are very few choices possible, and so it is possible to determine, for instance, that \(\chi(K_n) = n\) since each vertex must have a different color than the rest. The minimality component of chromatic numbers is useful for proving many basic theorems quickly, as it allows a focus on extreme, instead of general, cases (here, graph colorings that minimize the number of colors). It is for precisely that reason that mathematicians prefer such definitions.
A graph \(G\) is called \(k\)-colorable if there exists a graph coloring on \(G\) with \(k\) colors. If a graph is \(k\)-colorable, then it is \(n\)-colorable for any \(n > k\). A graph has a chromatic number that is at least as large as the chromatic number of any of its subgraphs. A graph has a chromatic number that is at most one larger than the chromatic number of a subgraph containing only one less vertex.
Consider the \(n^\text{th}\) cyclic graph \(C_n\) where \(n > 2\). Prove that
\[\chi(C_n) = \begin{cases} 2 & \text{if } n \text{ is even} \\ 3 & \text{if } n \text{ is odd.} \end{cases}\]
Suppose \(n\) is even. Then, \(\chi(C_n) \ne 1\) since there are two adjacent edges in \(C_n\). But a graph coloring for \(C_n\) exists where vertices are alternately colored red and blue, so \(\chi(C_n) = 2\).
Suppose \(n > 2\) is odd. Then, \(\chi(C_n) \ne 1\) since there are two adjacent edges in \(C_n\). Furthermore, \(\chi(C_n) \ne 2\) since vertex colors cannot alternate, as the final vertex to be colored will be adjacent to both a red and a blue vertex. But a graph coloring for \(C_n\) exists where \(n - 1\) vertices are alternately colored red and blue and the final vertex is colored yellow, so \(\chi(C_n) = 3\). \(_\square\)
Suppose a graph \(G\) and a graph \(G'\) are combined to create a graph \(H\) by connecting each vertex of \(G\) to each vertex of \(G'\) and otherwise all vertices and edges remaining unchanged. Prove that \(\chi(G) + \chi(G') = \chi(H).\)
Let \(G\) have a graph coloring with colors \(\{1, \, \dots, \, \chi(G)\}\) and \(G'\) have a graph coloring with colors \(\{\chi(G) + 1, \, \dots, \, \chi(G) + \chi(G')\}\). Then, color the vertices in \(H\) from \(G\) and \(G'\) accordingly with colors \(\{1, \, \dots, \, \chi(G) + \chi(G')\}\). Since no vertices of \(G\) and \(G'\) are the same color, this constitutes a graph coloring of \(H\), implying \(\chi(H) \le \chi(G) + \chi(G')\).
Now, consider a minimal graph coloring of \(H\). Suppose there are \(n\) colors among the vertices from \(G\), and suppose there are \(m\) colors among the vertices from \(G'\). Because every vertex in \(G\) is adjacent to every vertex in \(G'\), the two vertex sets cannot have any color in common. So this graph coloring of \(H\) has precisely \(n + m\) colors. But note that \(n \ge \chi(G)\) and \(m \ge \chi(G')\) as otherwise the chromatic number would not be minimal (the subgraph of vertices from \(G\) in \(H\) is precisely \(G\); likewise for \(G'\)). So \(\chi(H) = n + m \ge \chi(G) + \chi(G')\).
It follows that \(\chi(G) + \chi(G') = \chi(H).\) \(_\square\)
Chromatic Polynomial
The chromatic polynomial \(P_G\) of a graph \(G\) is a polynomial that, for each natural number \(k\), returns the number \(P_G(k)\) of \(k\)-colorings of \(G\). \(\chi(G)\) is the smallest positive integer that is not a root of \(P_G\). The degree of \(P_G\) is equal to the number of vertices of \(G\).
Consider an acyclic graph \(T_n\) on \(n\) vertices (also known as a tree). Prove that \(P_{T_n}(k) = k (k-1)^{n-1}\).
Consider an arbitrary vertex of \(T_n\). There are \(k\) possible colors for it. Now, consider each of its neighbors; there are \(k-1\) possible colors for each of them. Then, the neighbors of each of those vertices also has \(k-1\) possible colors, and so on. There will never be any further restrictions on a vertex's color, since the graph contains no cycles. Thus, there are \(k\) choices for the first vertex and \(k-1\) choices for each of the \(n-1\) subsequent vertices; there are a total of \(P_{T_n}(k) = k (k-1)^{n-1}\) choices. \(_\square\)
Edge Colorings
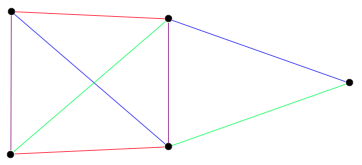 A proper edge coloring with 4 colors
A proper edge coloring with 4 colors
The most common type of edge coloring is analogous to graph (vertex) colorings. Each edge of a graph has a color assigned to it in such a way that no two adjacent edges are the same color. Such a coloring is a proper edge coloring. With cycle graphs, the analogy becomes an equivalence, as there is an edge-vertex duality. In general, however, the chromatic number is not related to the minimal \(k\) such that a proper edge \(k\)-coloring exists.
Another type of edge coloring is used in Ramsey theory and similar problems. In such cases, edges of the graph are colored one of \(k\) colors and mathematicians investigate the resulting colored graph substructures to determine what sizes of complete subgraphs exist.
A final type of edge coloring is used in the study of spanning trees. Edges are colored in such a way that there does not exist a cycle of the same color, and the minimal number of colors required for such an edge coloring of a given graph is known as its arboricity.
Prove that any planar graph has an edge coloring of at most three colors in which adjacent edges of the same color are allowed but cycles of edges of the same color are not.