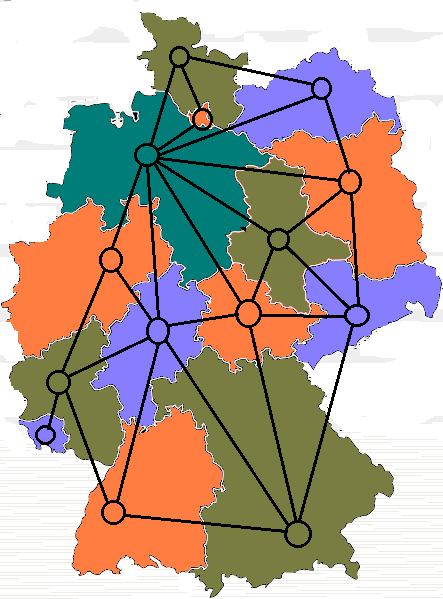
Graph Theory
Graph theory is the study of mathematical objects known as graphs, which consist of vertices (or nodes) connected by edges. (In the figure below, the vertices are the numbered circles, and the edges join the vertices.)
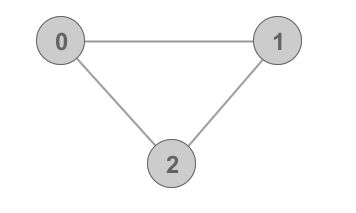 A basic graph of 3-Cycle
A basic graph of 3-Cycle
Any scenario in which one wishes to examine the structure of a network of connected objects is potentially a problem for graph theory. Examples of graph theory frequently arise not only in mathematics but also in physics and computer science.
Terminology
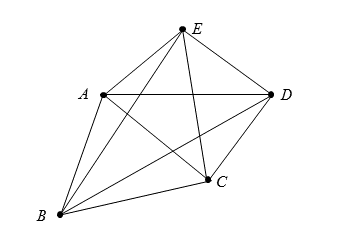
A non-trivial graph consists of one or more vertices (or nodes) connected by edges. Each edge connects exactly two vertices, although any given vertex need not be connected by an edge. The degree of a vertex is the number of edges connected to that vertex. In the graph below, vertex \( A \) is of degree 3, while vertices \( B \) and \( C \) are of degree 2. Vertex \( D \) is of degree 1, and vertex \( E \) is of degree 0.

Note: If the degree of each vertex is the same for a graph, we can call that the degree of the graph.
A graph in which it is possible to reach any vertex by traversing the edges from one vertex to another is said to be connected. The set of edges used (not necessarily distinct) is called a path between the given vertices. The graph above is not connected, although there exists a path between any two of the vertices \( A \), \( B \), \( C \), and \( D \).
A graph is said to be complete if there exists an edge connecting every two pairs of vertices. The graph above is not complete but can be made complete by adding extra edges:
Find the number of edges in a complete graph with \( n \) vertices.
Finding the number of edges in a complete graph is a relatively straightforward counting problem. Consider the process of constructing a complete graph from \( n \) vertices without edges. One procedure is to proceed one vertex at a time and draw edges between it and all vertices not connected to it. First, \( n-1 \) edges can be drawn between a given vertex and the \( n-1 \) other vertices. Next, \( n-2 \) edges are available between the second vertex and \( n-2 \) other vertices (minus the first, which is already connected). In general, each successive vertex requires one fewer edge to connect than the one right before it. As a result, the total number of edges is
\[ (n - 1) + (n - 2) + \cdots + 2 + 1 = \frac{n(n-1)}{2}. \]
Equivalently, the number of ways to to select two vertices (for which an edge must exist to connect them) is
\[ \dbinom{n}{2} = \frac{n(n-1)}{2}.\ _\square \]
For various applications, it may make sense to give the edges or vertices (or both) some weight. For instance, one can consider a graph consisting of various cities in the United States and edges connecting them representing possible routes between the cities. If one is interested in finding the shortest physical path to travel between the cities, it makes sense to weight the edges by the physical distance between the cities.
Graphs can also be directed or undirected: each edge in a directed graph can point to one or both nodes (for instance, representing one-way travel).
Most of the rest of this article will be concerned with graphs that are connected, unweighted, and undirected.
Eulerian Graphs
There are many types of special graphs. One commonly encountered type is the Eulerian graph, all of whose edges are visited exactly once in a single path. Such a path is known as an Eulerian path. It turns out that it is quite easy to rule out many graphs as non-Eulerian by the following simple rule:
A Eulerian graph has at most two vertices of odd degree.
To see why this fact is true, consider that it is possible to traverse all the edges connected to a vertex of odd degree only if one starts or ends on that vertex during a traversal. Otherwise, one must always enter and exit a given vertex, which uses two edges. However, the entry and exit vertices can be traversed an odd number of times. It is therefore not possible for there to be more than two such vertices, or else one would get "stuck" at some point during an attempted traversal of the graph.
The classic Eulerian graph problem is that of the seven bridges of Königsberg, which Euler solved in 1736.
Seven bridges of Königsberg:

The city of Königsberg is connected by seven bridges, as shown. Is it possible to visit all parts of the city by crossing each bridge exactly once?
First, we represent the different parts of the city as vertices and each bridge as a vertex connected two parts of the city, as shown below.
The graph contains more than two vertices of odd degree, so it is not Eulerian. Therefore, crossing each bridge exactly once is impossible. \(_\square\)
An analogous type of graph is the Hamiltonian path, one in which it is possible to traverse the graph by visiting each vertex exactly once. In general, computing the Hamiltonian path (if one exists) is not a straightforward task.
Planar Graphs
A graph is said to be planar if it can be drawn on a flat plane without any of the edges crossing. If so, one can define a face of the graph as any region bounded by edges and containing no edges on the interior. One important result regarding planar graphs is as follows:
Euler's Formula
Suppose a planar graph has \( V \) vertices, \( F \) faces, and \( E \) edges. Then
\[ V - E + F = 2. \]
Graph Coloring
One important problem in graph theory is that of graph coloring. Suppose each vertex in a graph is assigned a color such that no two adjacent vertices share the same color. Clearly, it is possible to color every graph in this way: in the worst case, one could simply use a number of colors equal to the number of vertices. (Indeed, for a complete graph, the minimum number of colors is equal to the number of vertices.) Of particular interest is the minimum number of colors \( k \) needed to avoid connecting vertices of like color, which is known as the chromatic number \( k \) of the graph. Equivalently, the graph is said to be \( k \)-colorable.

In particular, when coloring a map, generally one wishes to avoid coloring the same color two countries that share a border. The problem of map coloring neatly reduces to a graph coloring problem: simply represent each country by a vertex, with an edge connecting each pair of countries that share a border. In 1976, Appel and Haken proved the four color theorem, which holds that no graph corresponding to a map has a chromatic number greater than 4.