Interest Rate
Interest is the price of money. It is an additional payment paid by a borrower to an investor or lender beyond repaying the amount borrowed. For instance, a borrower may borrow \(\$100\) and agree to pay an additional \(\$5\) in interest above and beyond the \(\$100\) owed. An interest rate is the amount of that payment over a specified term. For instance, if the previous borrower agrees to pay back the \(\$100\) owed in one year's time, then the annual interest rate is \(5\%\).
Interest rates can be simple, meaning calculated once off the principal owed, or compounded, meaning calculated off the principal owed plus interest accrued. And compound interest can be calculated discretely, every month for instance, or continuously.
Einstein is reported to have said that compound interest is the most powerful force in the universe, implying that investments can grow to unexpected sizes over time or debts can balloon to unmanageable amounts because of compound interest. Many underappreciate the possibilities of investing over the long term, let alone how governmental monetary policies change interest rates to affect markets.
If you are 20, and invest $1,000 today in an investment that returns 5% a year, compounding. When you are 70, 50 years later, will your investment be worth more or less than 10 times your initial investment (ignoring inflation)? Will your investment be worth more or less than $10,000?
Contents
Simple Interest
Simple interest (SI) can occur either when a person borrows money or invests it. When a borrower receives a certain sum of money over a period of time, they agree to pay it back, along with a fee, known as the interest owed. Interest in an investment is the money one can earn by initially investing some money (called principal) and receiving a return on that investment. The return is a percentage of the principal (interest) and is added to the principal, making the initial investment grow.
Simple Interest is a type of interest that is applied to the amount borrowed or invested for the entire duration of the loan, without taking any other factors into account, such as past interest (paid or charged) or any other financial considerations. Simple interest is paid only on the original principal, it does not compound. Simple interest is generally applied to short-term loans, usually one year or less, that are administered by financial companies, or money invested for a similarly short period of time.
Simple interest (SI) is calculated by using the formula
\[SI=\dfrac{P \times R \times T}{100}.\]
Here \(P\) is principal amount, \(R\) is rate of interest, and \(T\) is time period of interest. The final amount to be paid is the initial principle plus the simple interest, \(P+SI\).
Here are some illustrations of the concept of simple interest through the following examples:
An invested sum fetched a total simple interest of 4016.25 rupees in 1 year at the rate of 9% per annum. What was the initial principal?
Let the principal amount be \(P\), rate of interest \(R\%\) per annum, \(SI\) the simple interest, and \(\text{T}\) the time period, then
\[\begin{align}
SI & = \dfrac{PRT}{100}\\ \\ 4016.25 & = \dfrac{P× 9 × 1}{100}\\ \\ \Rightarrow P & = \dfrac{4016.25 × 100}{9} =44625.\ _\square \end{align}\]
In how many years will an amount of Rs.1000 generate an equal return, if interest is \(10\%\) per annum?
(How many years will it take to double?)
Let the principal amount be \(\text{P}\), rate of interest be \(\text{R}\%\) per annum, \(\text{SI}\) be the simple interest, and \(\text{T}\) be the time period. Then
\[\begin{align}
\text{SI} & = \dfrac{\text{PRT}}{100}\\ \\ \require{cancel}{\cancel{\text{P}}} & = \require{cancel}{\dfrac{\cancel{\text{P}}\text{RT}}{100}} \qquad \left(\text{because P = SI}\right)\\ \\ 1 & = \dfrac{10 × \text{T}}{100}\\ \\ \Rightarrow \text{T} & = \dfrac{100}{10}=10.\ _\square \end{align}\]
A sum of money amounts to Rs.9800 after 5 years and Rs.12005 after 8 years at the same rate of simple interest. What is the rate of interest (in percent) per annum?
Let the principal amount be \(\text{P}\), rate of interest \(\text{R}\%\) per annum, \(\text{SI}\) the simple interest, and \(\text{T}\) the time period. Then
\[\begin{align} \text{SI for 3 years}&= \text{Rs.}(12005 - 9800) \\&= \text{Rs.}2205\\\\ \text{SI for 5 years}&= \text{Rs.}\dfrac{2205\times 5}{3} \\&= \text{Rs.}3675. \end{align}\]
Therefore, the principal is \((9800 - 3675) = 6125\) rupee, which implies
\[\begin{align} \text{T}&= \dfrac{3675 \times 100}{6125 \times 5}\\\\ &= 12.\ _\square \end{align}\]
Compound Interest
Typically interest rates on investments and loans are compound interest rates; the interest is not calculated off of just the initial principle but on the amount invested or owed at the time of the calculation. In this way, interest is said to compound. This works to an investor's advantage, allowing their returns to generate more returns, not just their initial investment.
Interest can be compounded discretely at many different time intervals. The number of and the distance between compounding periods are explicitly defined with discrete compounding. For example, interest that compounds on the first day of every month is discrete. Interest that is calculated at the end of the year is said to "compound annually," interest that is calculated at the end of the month is said to "compound monthly," and so on. Interest can also compound continuously.
Suppose that you open an account at the beginning of Year 1 with a principal of \(\$1000\), and that the bank provides an annually compounding interest rate of \(5\%\) (this is much higher than most savings rates today). At the end of the year, the bank will add \(\$50\) to your account, and your new balance will be \(\$1050\).
At the end of Year 2, instead of using the original balance of \(\$1000\), the bank will use the new balance of \(\$1050\) to determine the interest. They multiply \(\$1050 \times 5\% = \$52.50\). This is \(\$2.50\) more interest than you earned last term.
At the end of Year 3 the new balance will be \(\$1102.50\). So to figure that term's interest, the bank uses that new, higher balance instead of the original \(\$1000\) balance, now earning \(\$55.12\) (if they truncate). See how this works in favor of the person making the interest? The interest builds up much more quickly because the bank is using a higher balance every year to calculate the new interest.
The formula for calculating the amount returned when interest is compounded annually is
\[\text{A} = \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{\text{t}},\]
where \(\text{A}\) is the amount obtained, \(\text{P}\) is the principal amount, \(\text{R}\) is the rate of interest, and \(\text{t}\) is the number of times the interest compounds in this time period (for annual compounding this is the number of years). Then, the total compound interest over the term calculated is
\[\text{Compound Interest} = \text{A} - \text{P}.\]
Interest at the end of the first year is \[\begin{align} \dfrac{{\text{P}}_1\text{RT}}{100} &= \dfrac{\text{PR} × 1}{100}\\ \\ &= \dfrac{\text{PR}}{100}. \end{align}\] So, the amount at the end of the first year is \[\begin{align} {\text{P}}_1 + {\text{I}}_1 &= \text{P} + \dfrac{\text{PR}}{100}\\ \\ &= \text{P}\left(1 + \dfrac{\text{R}}{100}\right). \end{align}\] Interest at the end of the second year is \[\begin{align} \dfrac{{\text{P}}_2\text{RT}}{100} &= \dfrac{\text{P}\left(1 + \dfrac{\text{R}}{100}\right)\text{R×1}}{100}\\ \\ &= \text{P}\left(1 + \dfrac{\text{R}}{100}\right)\dfrac{\text{R}}{100}. \end{align}\] So, the amount at the end of two years is \[\begin{align} {\text{P}}_2 + {\text{I}}_2 &= \text{P}\left(1 + \dfrac{\text{R}}{100}\right) + \text{P}\left(1 + \dfrac{\text{R}}{100}\right)\dfrac{\text{R}}{100}\\ \\ &= \text{P}\left(1 + \dfrac{\text{R}}{100}\right)\left(1 + \dfrac{\text{R}}{100}\right)\\ \\ &= \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{2}. \end{align}\] Interest at the end of the third year is \[\begin{align} \dfrac{{\text{P}}_3\text{RT}}{100} &= \dfrac{\text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{2}\text{R×1}}{100}\\ \\ &= \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{2}\dfrac{\text{R}}{100}. \end{align}\] So, the amount at the end of three years is \[\begin{align} {\text{P}}_3 + {\text{I}}_3 &= \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{2} + \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{2}\dfrac{\text{R}}{100}\\ \\ &= \text{P}\left(1 + \dfrac{\text{R}}{100}\right)\left(1 + \dfrac{\text{R}}{100}\right)\left(1 + \dfrac{\text{R}}{100}\right)\\ \\ &= \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{3}. \end{align}\] So, we see that the amount in each case follows a geometric progression with first term \(\text{P}\) and common ratio \(\left(1 + \dfrac{\text{R}}{100}\right).\)Therefore, the amount at the end of the \(n^{\text{th}}\) year is the\({(n + 1)}^{\text{th}}\) term of the geometric progression, which is
\[\text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{n + 1 - 1}= \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{n}.\ _\square \]
Find the interest on Rs.500 for 2 years if the interest is compounded annually at a rate of \(5\%\) per annum.
Let \(\text{A}\) be the amount obtained, \(\text{P}\) the principal amount, \(\text{R}\) the rate of interest, \(\text{t}\) the time period, and \(\text{CI}\) the compound of interest. Then
\[\begin{align}
\text{A} & = \text{P}{\left(1 + \dfrac{\text{R}}{100}\right)}^{\text{t}}\\ \\ & = 500 × {\left(1 + \dfrac{5}{100}\right)}^{2}\\ \\ & = 500 × {\left(\dfrac{21}{20}\right)}^{2}\\ \\ & = 500 × \dfrac{441}{400}\\ \\ & = 551.25\\ \\ \text{CI} & = \text{A} - \text{P}\\ & = 551.25 - 500\\ & = 51.25.\ _\square \end{align}\]
What would Rs.100 amount to in a year if the interest is compounded at a rate of \(10\%\) half-yearly (every six months)?
Let \(\text{A}\) be the amount obtained, \(\text{P}\) the principal amount, \(\text{R}\) the rate of interest, and \(\text{t}\) the number of times that interest compounds. Then
\[\begin{align}
\text{A} & = \text{P}{\left(1 + \dfrac{\text{R}}{200}\right)}^{\text{t}}\\ \\ & = 100 × {\left(1 + \dfrac{10}{200}\right)}^{2}\\ \\ & = 100× {\left(\dfrac{21}{20}\right)}^{2}\\ \\ & = 100 × \dfrac{441}{400}\\ \\ & = \dfrac{441}{4}\\ \\ & = 110.25.\ _\square \end{align}\]
Try the following problems:
Continuously Compounded Interest
Discrete and continuous compoundings are closely related terms. An interest rate is discretely compounded whenever it is calculated and added to the principal at specific intervals (such as annually, monthly or weekly). Continuous compounding means that an amount is always said to be "accruing" interest. Continuously compounding interest uses a natural log-based formula (natural logs being logarithms with a base of \(e\)) to calculate and add back accrued interest at the smallest possible intervals.
Continuously compounded interest means that principal is constantly earning interest with the interest immediately calculating and compounding. Graphically, it can be demonstrated as below.
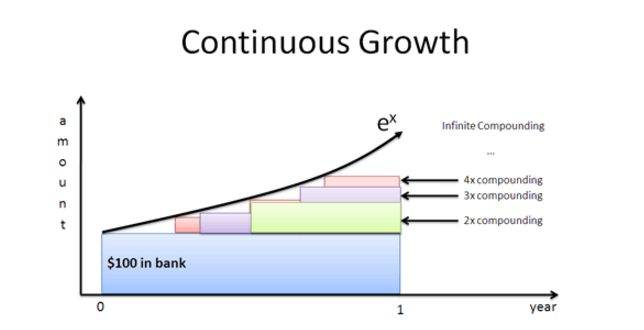
Mathematically, continuously compounding interest can be expressed as follows:
\[\begin{aligned} \text{A} &= \text{P}e^{\text{rt}}, \end{aligned}\]
where \(A\) represents the total amount at a given time, \(P\) represents the initial principal, \(r\) is interest rate (expressed as a decimal), and \(t\) is the time.
This is similar to taking the discrete compound interest formula
\[\text{A} = \text{P}\Big (1+\frac{\text{r}}{x}\Big )^{x\text{t}},\]
where \(A\) represents the amount earned, \(P\) represents the initial principal, \(r\) is interest rate, \(x\) is the number of times the interest is credited in a year, and \(t\) is the time. Then transforming it from discrete to continuous by taking \(x\rightarrow \infty\), that is "constantly earning interest with the interest immediately calculating and compounding":
\[\begin{aligned} \text{A} &= \text{P} \lim_{x\rightarrow \infty}\Big (1+\frac{\text{r}}{x}\Big )^{x\text{t}} \\\\ &= \text{P}e^{\text{rt}}. \end{aligned}\]
If you invest $2400 at an annual interest rate of 10% compounded continuously, calculate the final amount you will have in the account after 5 years.
Let \(\text{P}\) be the principal amount, \(\text{A}\) the amount, \(r\) the interest rate, and \(t\) the time period. Then
\[\begin{align}
\text{A} & = \text{P}e^{\text{rt}}\\ & = 2400 × e^{\tfrac{10×5}{100}}\\ & = 2400 × e^{0.5}\\ & = 2400 × 1.6487\\ & = 3956.93.\ _\square \end{align}\]Note: 10% annual interest compounded discretely for five years on a principal of $2400 would result in a total of $3865.22, a difference of $91.70. \(_\square\)
Rule of 72
The rule of 72 states that at \(r\%\) annual interest rate, an investment would take approximately \(\frac{72}{r}\) years to double.
Solve for \(\text{t}\) from the exponential equation:
\[\begin{aligned} \text{A} &= \text{P}{\left(1 + r\% \right)}^{\text{t}} \\ 2\text{P} &= \text{P}{\left(1 + r\% \right)}^{\text{t}} \\
\ln 2 &= \text{t}\ln (1+r\%) \\ \text{t} &= \frac{\ln 2}{\ln (1+r\%)}. \end{aligned}\]Applying the Maclaurin series to \(\ln (1+ r\%) = r\% + \ldots\) and using \( \ln 2 \approx 0.69 \), we obtain
\[ \frac{ \ln 2 } { \ln (1+r \%) } \approx \frac{ 0.69} { r\%} = \frac{69}{r}. \]
We then change the numerator slightly to \(72\), because \(72\) is easier to divide for small values of \(r\). \(_\square\)
What is the error of applying rule of 72 with the actual calculation for an annual interest rate of \(9\%\)?
From rule of 72,
\[t=\frac{72}{9}=8.\]
Actual result is
\[t=\frac{\ln{2}}{\ln(1+0.09)} = 8.04.\]
The error is calculated with the formula \(\frac{8.04-8}{8.04}\times 100\%=0.50\%\). \(_\square\)
Below is the analysis table for the accuracy of rule of 72.
| Rate of Interest (\(r\)) | Rule of 72 | Actual Number | Difference | Error |
| \(1\%\) | 72 | 69 | 3 | \(+4.35\%\) |
| \(2\%\) | 36 | 35 | 1 | \(+2.86\%\) |
| \(3\%\) | 24 | 23.4 | 0.6 | \(+2.56\%\) |
| \(5\%\) | 14.4 | 14.2 | 0.2 | \(+1.41\%\) |
| \(8\%\) | 9 | 9.01 | 0.01 | \(-0.11\%\) |
| \(12\%\) | 6 | 6.12 | 0.12 | \(-1.96\%\) |
| \(16\%\) | 4.5 | 4.67 | 0.17 | \(-3.64\%\) |
| \(25\%\) | 2.88 | 3.11 | 0.23 | \(-7.40\%\) |
| \(50\%\) | 1.44 | 1.71 | 0.27 | \(-15.79\%\) |
| \(72\%\) | 1 | 1.27 | 0.27 | \(-21.26\%\) |
| \(100\%\) | 0.72 | 1.00 | 0.28 | \(-28.00\%\) |
For an error margin between \(-3\%\) and \(+3\%\), the rule of 72 is fairly accurate for rate of interest in range 2%~16%, which turns out to be most of the cases in real world.
As \(r\) increases, the approximation from Maclaurin series starts to diverge. Hence, this provides a way of estimating the extent of error. For example, since \( \ln ( 1 + r ) = r - \frac{r^2}{2} + \cdots \), the approximation by \(r\%\) introduces an error of \( \frac{r^2}{2} \% \).
For more details, see this discussion.
Annual Percentage Rate (APR)
The annual percentage rate (APR) of a loan is the cost of the credit per year, expressed as a percentage of the loan amount. It is the annual rate that is charged for borrowing (or made by investing), expressed as a single percentage number that represents the actual yearly cost of funds over the term of a loan. It refers to the rate paid to a financial institution by a borrower.
For instance, a credit card might express their APR as \(20\%\). This means that a card holder who uses their credit card to make a $100 purchase, and does not pay it back for 365 days can expect to owe $20 in interest at the end of that time period.
APR does not specify the term that interest is compounded at, merely the annual rate of whatever the interest is (called the nominal interest rate) at whatever term length it's compounded plus fees and additional costs. Yes, this means that the APR is typically higher than just the nominal rate, as this includes any fees or additional costs associated with the transaction.
Annual Percentage Yield (APY)
The APY of a loan is the amount that is earned on an interest-bearing investment per year, expressed as a percentage of the total due. The APY is typically higher than the interest rate, as the interest is being compounded. However, it does not account for the possibility of account fees affecting the net gain. APY generally refers to the rate paid to a depositor by a financial institution.
The formula for calculating the APY is given as
\[\large \text{APY}=100 \left[ \left( 1 +\dfrac{\text{Interest}}{\text{Principal}} \right)^{\frac{365}{\text{Days in terms}}} -1 \right].\]

