Inverse Trigonometric Graphs

In this post, we study the graphs of inverse trigonometric functions. Before reading this post, you may wish to review graphs of basic trigonometric functions and introduction to inverse trigonometric functions.

As we can see from the graph of the sine function, many different angles $\theta$ map to the same value of $\sin(\theta)$:

For example,

$$0 = \sin 0 = \sin \pi = \sin 2\pi = \cdots = \sin k \pi$$

for any integer $k$. To overcome the problem of having multiple values map to the same angle for the inverse sine function, we will restrict our domain before finding the inverse. The domain and ranges of the basic inverse trigonometric functions are as follows:

$$\begin{array}{|c|c|c|} \hline \text{Function} & \text{Domain} & \text{Range}\\ \hline \sin^{-1} x & [-1, 1] & \left[- \frac{\pi}{2}, \frac{\pi}{2} \right]\\ \hline \cos^{-1} x & [-1, 1] & \left[ 0, \pi \right]\\ \hline \tan^{-1} x & (-\infty, \infty) & \left(- \frac{\pi}{2}, \frac{\pi}{2} \right)\\ \hline \end{array}$$

The graphs of the inverse functions are the original function in the domain specified above, which has been flipped about the line $y=x$. The effect of flipping the graph about the line $y=x$ is to swap the roles of $x$ and $y$, so this observation is true for the graph of any inverse function.

Now, by swapping the roles of $x$ and $y$, the domain of the sine function gets converted to the range of the $\sin^{-1}$ function and vice versa. The following graph demonstrates that the domain of $\sin^{-1}$ is $[-1, 1]$ and the range of $\sin^{-1}$ is $\left[- \frac{\pi}{2}, \frac{\pi}{2} \right]:$

$\sin^{-1}$

Similarly, for the cosine function, the domain of the cosine function gets converted to the range of the $\cos^{-1}$ function and vice versa. The following graph demonstrates that the domain of $\cos^{-1}$ is $[-1, 1]$ and the range of $\cos^{-1}$ is $\left[ 0, \pi \right]:$

$\cos^{-1}$

For the tangent function, the domain of $\tan^{-1} x$ is $(-\infty, \infty)$ since the tangent has both positive and negative vertical asymptotes, and the range of $\tan^{-1}x$ is $\big(- \frac{\pi}{2}, \frac{\pi}{2} \big):$

$\tan^{-1}$

Plot the graph of the inverse function of tangent, $\tan^{-1} \theta,$ and describe the behavior of the asymptotes of this graph.

---

Since the inverse function is obtained by reflecting the graph about the line $y=x$, the vertical asymptotes of the tangent function become horizontal asymptotes of the inverse tangent function. As $\theta$ approaches $-\infty$, $\tan^{-1} \theta$ approaches $-\frac{\pi}{2}$; as $\theta$ approaches $\infty$, $\tan^{-1} \theta$ approaches $\frac{\pi}{2}$.

By reflecting the graph, we have the following graph of the inverse tangent function:

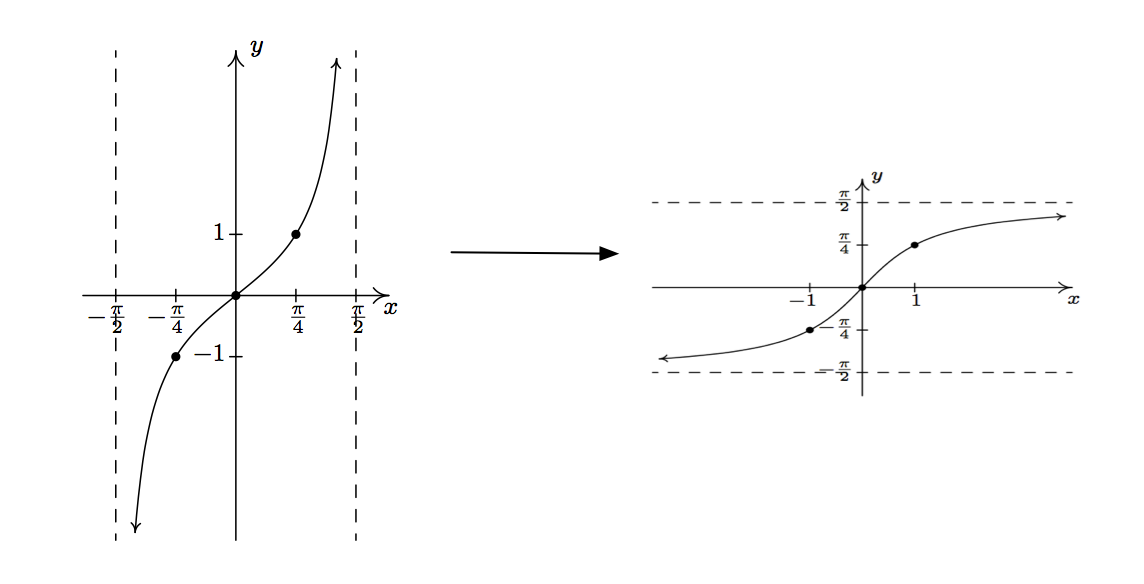
Try this for practice!

Consider the graphs of $\sin^{-1} x$ and $\tan^{-1} x$.

Do these graphs satisfy any properties of symmetry?
Are these functions either even, odd, or neither?

---

Since both the graphs of $\sin^{-1} x$ and $\tan^{-1} x$ are symmetric about the origin, these functions are both odd functions. $_\square$