Does \(\sqrt{x^2+y^2}=x+y?\)
This is part of a series on common misconceptions.
Is this conception true or false?
\[\large \sqrt{a^2 + b^2} = a + b\]
Why some people say it's true: It's an example of the distributive property which works since exponents are just repeated multiplication. So, just like \(5(a+b) = 5a + 5b, \sqrt{a^2 + b^2} = \sqrt{a^2} + \sqrt{b^2} = a + b.\)
Why some people say it's false: The distributive property doesn't work for the square root functions, so you can't say that \(\sqrt{a^2 + b^2} = \sqrt{a^2} + \sqrt{b^2}\).
The statement is \( \color{red}{\textbf{false}}\).
Proof 1: Provide a counter example.
Let \( a = 3 , b = 4 \).
Then, \( LHS = \sqrt{ 3^2 + 4^2 } = \sqrt{ 25 } = 5 \).
However, \( RHS = 3 + 4 = 7 \).
Hence, we do not have an identity.Proof 2: By contradiction. Let's assume that the identity is true.
If we square both sides, we obtain
\[ a^2 + b^2 = (a+b)^2 = a^2 + 2ab + b^2. \]
This is clearly not an identity since \( 2ab \) is not always 0. Thus, we can conclude that this is an identity if and only if \( 2ab = 0 \).
Proof 3: Geometric interpretation
We can also look at this geometrically and immediately see that it is false:
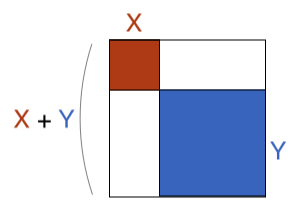
Understanding why the distributive property does not hold for square roots:
The distributive property is an identity that relates addition and multiplication: \(m(a+b) = ma + mb\). However, it does not apply to the square root function. To understand why, consider the shape of the square-root function:

Consider any two points on this curve, \((a, \sqrt{a})\) and \((a+b, \sqrt{a+b})\), for \(b > 0\). What is the effect on the difference between \(\sqrt{a}\) and \(\sqrt{a+b}\) as the two points shift together, along the function and to the right (in other words, as \(a\) increases, but \(b\) remains fixed)?

As the region shifts to the right, the \(\sqrt{x}\) curve flattens out, which, algebraically, means that the difference between \(\sqrt{a}\) and \(\sqrt{a+b}\) drops to 0 as \(a\) increases and \(b\) stays constant. On the other hand, the difference between \(\sqrt{a}\) and \(\sqrt{a} + \sqrt{b}\) is always \(\sqrt{b}\), which doesn't change of course, as the region shifts right, since \(b\) doesn't change.
Rebuttal: For the most part, I agree, but \(\sqrt{x^2} = \pm x,\) not \(|x|\).Reply: That's another misconception. See the "\(\text{Is }\sqrt{x^2} = \pm x?\)" misconception page for details.
Rebuttal: Consider a linear function, \(f(x) = mx +b\). As a region defined by two points a fixed width apart moves right, it stays the same height; does that mean that all linear functions obey the distributive property? (That is, if \(f(x) = mx + c\) for any real number \(c,\) then \(f(a+b) = f(a) + f(b).\))
Reply: No. There's actually a second condition in order for the distributive property to be applicable to a function: \(f(0)\) must equal 0. Otherwise, \(f(a) = f(a+0) = f(a) + f(0)\) could not possibly be true. Therefore, functions of the form \(f(x) = mx + b\) only obey the distributive property on the domain of real numbers if \(b=0\).
Sherry is excited to learn about the distributive law, and thinks that it applies to every possible operation. As such, she claims that
\[ \sqrt{a^2+b^2} = \sqrt{a^2} + \sqrt{b^2} .\]
How many ordered pairs of integers \( (a, b) \) are there, such that \( -10 \leq a \leq 10, -10 \leq b \leq 10 \) and
\[ \sqrt{ a^2 + b^2} = \sqrt{a^2} + \sqrt{b^2} ?\]
See Also