Knots
Knots are tangible and useful in everyday life, but they are also a structure studied in depth by mathematicians. We will explore the mathematics of knots, links, and braids, and also study the knots you tie (perhaps multiple times) every day: your shoelaces!

Contents
Creating Knots
An easy way to make a knot is to take an (unclasped) necklace chain, make any loops and ties in it, and then clasp the ends together. This can also be done with a garden hose or piece of rope, where the final step is to glue the two ends together. Most necklaces are worn as a simple loop with no ties, which is a special case called an unknot.

Any knot that can be created from the unknot without tearing or cutting is also an unknot.
Try It Yourself: Starting with a rubber band or rope with ends glued together, which of the following knots can we make without tearing or cutting the rubber band?

Solution: The first three knots can be made by making a single twist in the rubber band, which shows these knots are unknots. It seems that the fourth knot truly crosses itself and cannot be made from a simple rubber band without cutting, but how can we prove this? We will see later how to use knot colorings to answer this question.
Knots and links are studied in topology, which studies properties that are unchanged by continuous transformations. Knots are examples of embeddings, since they are loops living in in 3-dimensional space.
A knot is a closed loop of string in three dimensional space. Two knots are equivalent if one can be continuously transformed into the other without any cutting or gluing.
Note the difference between mathematical knots and knots you tie in a shoelace or rope:
- mathematical knots are closed and there are no loose ends to tie or untie
- for mathematical purposes, we imagine the string or rope as having no thickness
- to get a mental picture of continuous transformation, imagine that the knot is made of an elastic material that can be moved around, stretched, or shrunken as much as you like without breaking or tearing.
Instead of studying knots in three dimensions, it is sometimes easier to study the two-dimensional shadows cast by these knots. A knot diagram captures the closed loop of a knot by drawing either an over strand or an under strand at the crossing positions. The simplest nontrivial knot is a circle that winds through itself, called the trefoil knot. It also comes in two forms: left-handed and right-handed configurations, which are mirror images of each other.

There may be more than one way to draw a knot using a knot diagram. We consider the following two questions:
- Given a knot diagram, is the knot equivalent to the unknot?
- Given two knot diagrams, how can you tell if they represent the same knot?
To start with, we can describe some invariants of a knot, or properties that do not change even if drawn in multiple ways in different knot diagrams. One important indicator of knot complexity is the minimum number of crossings in any drawing of a given knot.
The crossing number of a knot is the minimum number of crossings in any drawing of the knot.
For example, the unknot has crossing number 0 and the trefoil knot has crossing number 3.
Try It Yourself: Can you make a knot with crossing number 1 or 2?
Is that a knot? Or not a knot?
In Example 1 above, we saw a few knots that are equivalent to the unknot. How can we show that the trefoil knot is not equivalent to the unknot? Let's first state the following theorem due to Reidemeister that shows when two diagrams represent the same knot type.
Reidemeister's Theorem: Two diagrams represent the same knot type if and only if the diagrams are related by performing a sequence of Reidemeister moves:

How does Reidemeister's theorem help us distinguish between the trefoil and unknot? Consider coloring a knot by three colors with each arc a single color such that
- The coloring uses at least two of the three colors
- Each crossing of three incident strands have all strands either the same color or all different colors.
A knot is said to be tricolorable if such a coloring exists. The following coloring shows the trefoil knot is tricolorable.

However, the unknot is not tricolorable (since it violates the first property). Now, the following theorem shows that tricolorability doesn't change upon performing Reidemeister moves.
A tricolorable knot diagram remains tricolorable under all Reidemeister moves.
Together with Reidemeister's Theorem, this shows that any diagram representing the trefoil knot is also tricolorable, implying that the unknot is not a diagram representing the trefoil knot.
Corollary: The unknot and trefoil knots are not equivalent knots.
Coloring can help us to distinguish knots that are tricolorable from those that are not tricolorable (such as the trefoil and the unknot), but does not help us distinguish other knots (such as the figure-eight knot from the unknot). To distinguish these knots, we need to explore other variants, such as polynomial invariants that we will explore in a later summary. By using these invariants, it can be proved that the left-handed and right-handed trefoil knots are not equivalent, so it is impossible to transform one to the other continuously without any breaking or tearing!
 There is a piece of string lying on the floor in the position shown above. We are too far away to tell which section of the string lies above or below at each of the crossovers at X, Y, and Z.
There is a piece of string lying on the floor in the position shown above. We are too far away to tell which section of the string lies above or below at each of the crossovers at X, Y, and Z.
If it is equally likely that either section lies on the top of each crossover, what is the probability that the string is actually knotted?
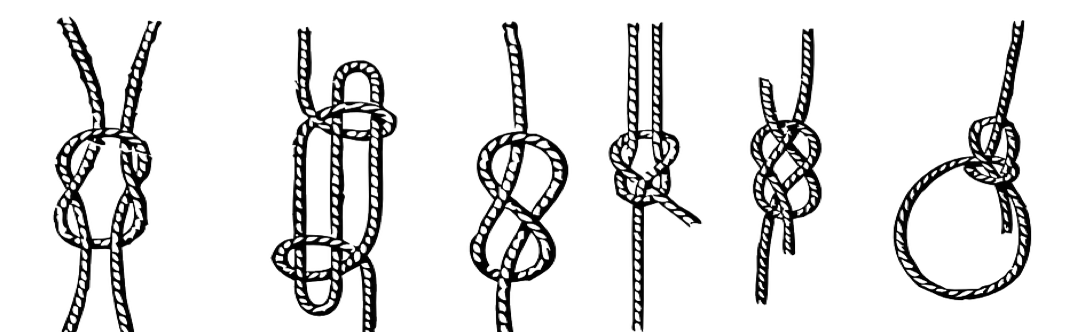
One way to classify knots is by creating tables of knots, labeled by knot properties such as crossing number. In Alexander-Briggs notation, a knot is labeled by its crossing number and the subscript is an index for each knot of that crossing number (ordered arbitrarily):

By gluing together the ends of the ropes in the following knots, can you identify the knots below with knots in the knot table? For the ropes with more than two ends, does it matter how the ends are glued together?
Links and braids
Links are made of multiple knotted components. The simplest link is the unlink, which is a disjoint union of unknots.
Try-it-Yourself: Using several pieces of string or rope, form the following sets of intersecting links:

We can also create links by taking several pieces of rope, braiding them together, then identifying the ends. The following diagram shows how to create a Hopf link by a braiding method:

And how to create a Figure 8 knot by braiding three pieces of rope:

Try it yourself: Can you create a trefoil knot by a braiding method?
Solution: The following diagram illustrates how to create a trefoil knot by braiding:
What are the differences between twisting the braid an odd number of times and an even number of times (comparing with the Hopf link)?
Try it yourself: Cut any single loop in the Borrommean rings and show that the other two loops become unlinked.

Is it possible to link 4 rings together such that cutting any single loop unlinks all the remaining loops?
Applications of Knots
How do you tie your shoelaces? Try the following exercise to determine the type of knot you use.
Are you a Granny Knot tier or a Square Knot tier?
Take a pair of shoes and without putting them on your feet, tie one of the shoes as if you are wearing them. If you are like most people, you start with a simple starting knot (which forms half a trefoil knot). Then on top of this, you make an "around the tree" type of knot by forming a loop with one lace and tying the other lace around this loop in one direction or the other.
Now that your shoe is tied, pull on the loops until the ends come out, and you should be left with two knots. How do your knots sit on top of each other? Are you a granny knot tier or a square knot tier?


Images courtesy Ian Fieggen fieggen.com
If you shake the shoe slightly and your shoelace bow sits vertically instead of horizontally across the shoe, then you are probably a granny knot tier. Granny knots are often also responsible for crooked bows on bow ties, gift wrapping, and hair ties.
How to fix this problem? To transform from a granny knot tier to a square knot tier, simply reverse the starting knot! If you currently tie your starting knot by threading the left shoelace over and through the right shoelace, then switch it to right shoelace over and through the left shoelace, proceed with the same "around the tree" knot, and Voila!

Images courtesy Ian Fieggen fieggen.com
If you have friends whose shoelaces are constantly coming undone, figure out if they are granny knot tiers. Especially if they are runners or rock climbers, they will thank you for showing them a more secure knot!
Join the discussion about Granny vs. Square shoelace tying here.
As another fun application of knots, consider making your morning bagel into a trefoil knot!
Knots in Art
Knots and links appear in art pieces and installations throughout the world.
 small
small
Celtic Serpent Knot in Dixon, Illinois. License Creative Commons 2.0 Wayne Wilkinson

M.C. Escher: Knot

Endless Knot
What knots have you seen in art?
